| 4 カラテオドリの外測度 | |
| f-denshi.com [目次へ] 最終更新日:04/11/29 | |
| サイト検索 | |
いよいよ,この章から ”ルベーグの面積” を抽象化して,本格的な測度論に踏み込んでいきます。
ユークリッド空間の部分集合 (=図形) で考えたルベーグの外測度,内測度なる概念を発展させて一般的な測度の概念を築きます。
[1]
|
定義 集合 X が与えられているとき,そのすべての部分集合 A に対して定まる非負実数への写像(=集合関数), m*: A ⇒ m*(A) が次の条件を満たすとき, (1) 0≦m*(A)≦∞ , m*(φ)=0 m* をカラテオドリの外測度という。 (3)が成り立つことをσ-劣加法性という。 |
これはルベーグの外測度に成り立つ関係,
(1) (2) (3)
を基にして,長さや面積がもつ性質のエッセンスを抽出したものです。 しかし,m*(A) について長さ,面積なる概念にとらわれる必要はありません。なお,このページで外測度というときはカラテオドリの外測度を意味することとします。
[2]
|
定義 外測度 m* が与えられている集合 X の部分集合 A がカラテオドリの可測であるとはすべての X の部分集合 E に対して, m*(E)=m*(E∩A)+m*(E∩Ac) ・・・・・・・ [*] が成り立つこととする。このとき,A をカラテオドリの可測集合という。 |
まず,注意すべきことは,ここでの可測集合は外測度だけで定義されていることです。 「内測度」なるものを議論の中に持ち込むことも可能ですが,結局,可測な集合を考えてゆくときは,ルベーグ測度でそうであったように,「外測度」=「内測度」=「測度」となるので,「内測度」なる概念は排除しているのです。
内測度は”挟み撃ち”を利用するリーマン積分を色濃く反映した概念で,本来,測度論では不要!ということ。
ここで,X を n次元ユークリッド空間とすれば,ここでいう可測集合とは ”ルベーグ可測な集合=ルベーグの面積” と一致します。 ルベーグ可測の定義 [#] をもう一度書くと,
「・・・ ,A を含む任意の半開区間 J ∈R2 に対して, |J|=m*(A)+m*(J∩Ac)が成り立つとき,A を ルベーグ可測な集合 といい,m*(A) を m(A) と書く。」
でした。
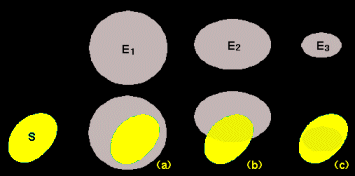
[3] このルベーグの定義と抽象化されたカラテオドリの定義とでどこが違うかといえば,「A を含む任意の半開区間 J 」 という文言が,「カラテオドリの定義」では, 「すべての X の部分集合E」 という文言に置き換わっていることです。 カラテオドリの可測性は下に示すような (a),(b),(c) で代表されるようないろいろな包含関係にある E を用いて,[*] に関する評価を行なっているのに対して,ルベーグ可測性は, (a) S⊂J (⇔ A⊂E) なる包含関係にある場合しか評価していません。
 |
⇔ |  |
| カラテオドリ的 | ルベーグ的 |
具体例: S を黄色で示した領域にある有理点の集合とすれば[*] は次のようになります。
| m*(E∩Sc) =色のついた 部分の面積 |
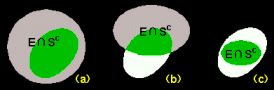 |
E∩Sc は, 灰:実数 と 緑:無理数 との和集合から成り立つ |
| + | ||
| m*(E∩S) =0 |
 |
E∩Sは, 黄:有理数 から成り立つ |
| || | ||
| m*(E) =水色部分 の面積 |
 |
水:実数 |
EとSとの包含関係が(a),(b),(c)の3つのどの場合についても,それぞれ,m*(E)=m*(E∩A)+m*(E∩Ac) が成り立つことを確認してください。
[4] 以上のような可測集合とカラテオドリの測度を定義すると,次の2つの定理が導かれます。まず,
|
定理 集合 X と外測度 m* が与えられたとき,その可測集合全体(=可測集合族)はσ加法族(ボレル集合体)となる。
|
||||||
ここで,外測度,可測集合はカラテオドリ測度のことです。また,σ加法族については,次ページ4. を参考にしてください。もう一つは,
|
定理 完全加法性: カラテオドリの可測集合列,A1,A2,・・・ が互いに共通部分を持たないならば, が成り立つ。 |
[証明] ⇒ [#] とりあえず,証明なしで。
以上,「外測度」と「可測集合」から「σ加法族 (ボレル集合体)」と「完全加法性」という概念が導き出されてくることを知ると,これら4つの間には密接な関係があるのでは?と推察するのは自然なことです。実際,
「 集合 X のσ加法族βを一つ定め(←可測空間という),その集合を用いて測度を導入する 」
というような公理体系が歴史的に受け入れられていったのです。つまり,ユークリッド空間で成り立つ定理からエッセンスを抽出する。そして,それを定義・公理として最初に提示し,それだけを元に演繹的に矛盾の無い一般化された体系を創りあげていくというプロセスです。
[5] カラテオドリの外測度の完備性について述べておきます。
|
測度空間の完備の定義 測度空間(X,β,m)が完備であるとは,任意のS⊂A∈βについて, m(A)=0 ⇒ S∈β が成り立つことである。 |
すると,
|
定理 カラテオドリの外測度から得られる測度空間は完備である。 |
証明
Xの任意の部分集合Eに対して,S⊂A,m(A)=0 ならば,
(E∩S) ⊂ (E∩A) ⊂ A
⇒ m*(E∩S) ≦ m*(A) ≦ m(A)=0
⇒ m*(E∩S) =0 ・・・ (1)
また,
E ⊃ (E∩Sc)
⇒ m*(E) ≧ m*(E∩Sc) ・・・ (2)
(1)+(2) ⇒ m*(E) ≧ m*(E∩S)+m*(E∩Sc)
⇔ Sは可測集合
|
定理 完備化 測度空間(X,β,m)において,B∈β が存在して, m( (A∩Bc)∪(Ac∩B) )=0 となる A⊂X の全体をβ’,m’(A)=m(B) とすると(X,β’,m’)は完備な測度空間となる。 |