205  畳み込み( コンボルーション )
f-denshi.com  更新日：

１．離散的な畳み込み

［１］　「畳み込み積分」の考え方を，「離散的なたたみ込み」の具体例で説明します。

くっまんす王国において，各時期に原発から放出された放射能の量が，


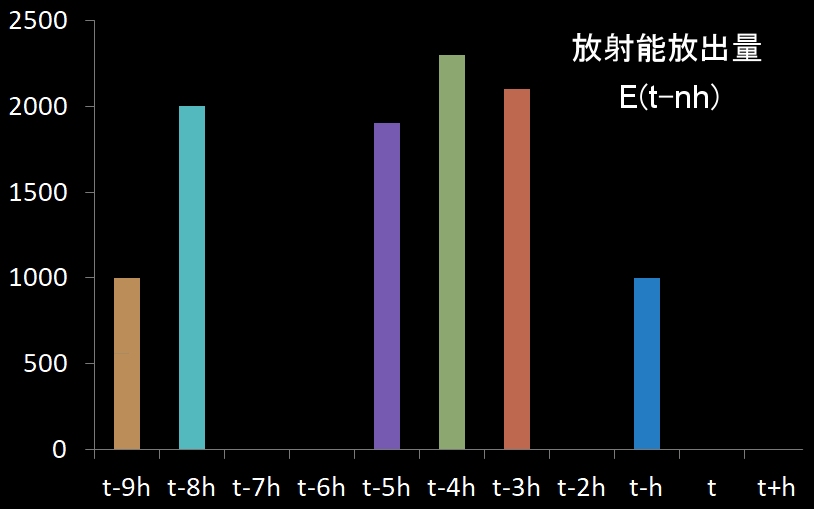
であることが分かっているとします。縦軸はバラ撒かれた放射能の量です。横軸は年代です。

そして，放射能の半減期が h であるとする，すなわち，下図，


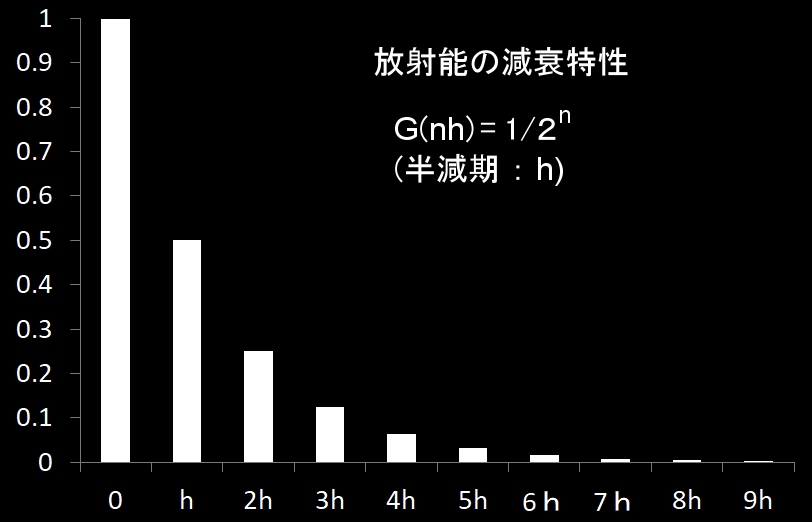
で放射能の減衰特性（応答関数）が与えられるとします。

［２］ すると，各時期に原発から飛散した放射能が減衰していく様子をすべてを描くと，下図のようになります。

このとき，ある年 t に，くっまんす王国に存在する放射能は，
下図の赤い囲みの中の放射能量をすべて加算すればよいことがわかります。


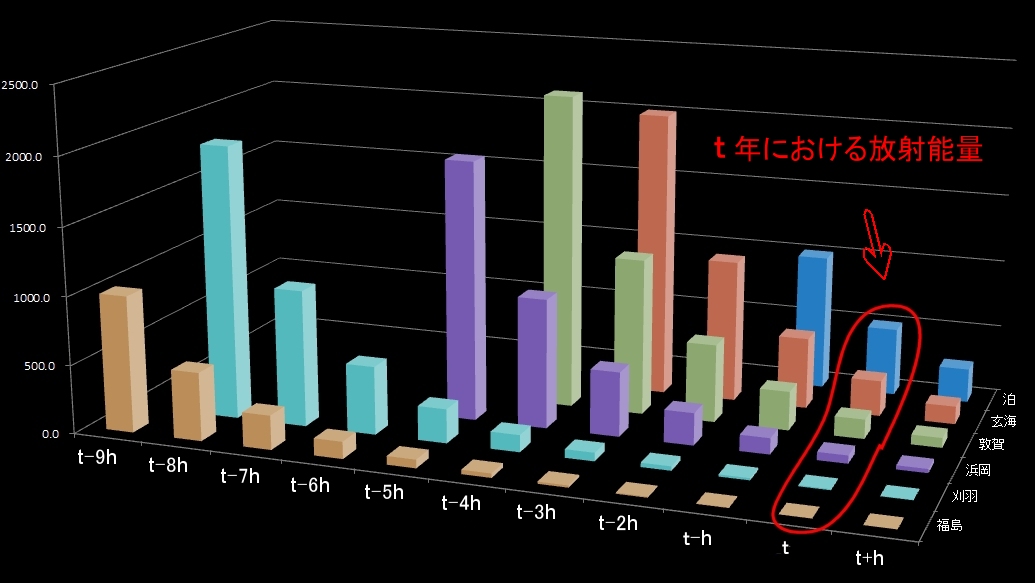
その放射能 P(t) の計算式は，上の図をよく見て，

P(t)＝E（t−9h)G(9h)＋E(t−8h）G(8h)＋E（t−5h)G(5h)
　　　　　　　　＋E(t−4h)G(4h)＋E（t−3h)G(3h)＋E(t−h）G(h)
　　＝ E（t−nh）G(nh)

と表記できることが分かります。

この計算規則こそが，「離散的な畳み込み」なのです。

［３］　この離散的な関係式を連続的な極限で考えたもの，つまり，
ばら撒かれる放射能 E ( t−τ) は，連続的に記録され，それぞれが同じ半減期で連続的に減衰していくとしたとき，
ある時刻における放射能の量は，

 P (t) ＝   E ( t−τ)G（τ）dτ　

と書き表すことができます。G（τ）=1/2τ は各イベント（事象）が起きてからの減衰を表すので，τ＜0　ではゼロの値をとる関数です。

これが，畳み込み積分の意味です



２．畳込みの定義（確率解釈）

物理的な描像：
　１次元ランダムウォーク　⇒ 拡散方程式も参照のこと [#]

［１］　畳み込みの定義です。

時刻 0 に原点 x＝0 にある粒子がX軸上をランダムに動いていく様子を考えます。このとき，時刻 ｔ において，微小範囲 (x，x＋Δx)に粒子が見つかる確率が確率分布関数，Pｔ(x) と Δx との積で，

Pｔ( x )Δx　　　←　P(x，t)Δx　と書いてもよい。

で与えられるものとします。特に，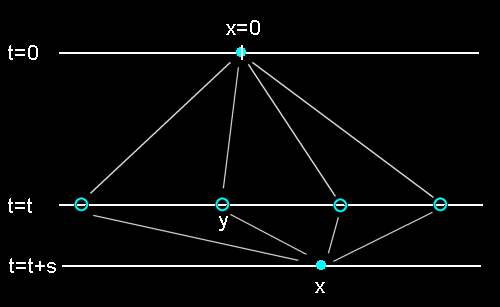

( I ) 時刻 ｔ＋s に微小範囲 (x，x＋Δx)に粒子が見つかる確率は，

Pｔ+s( x )Δx

となります。一方，これと同じ確率を，粒子の動きがランダムであることから時刻 t までとそれ以後の s 秒とを２つの独立な事象に分けて計算することも可能で，それは，

( II ) 時刻 ｔ に微小範囲 ( ｙ，y＋Δy )に確率 Pｔ( y )Δy で存在する確率と 時刻 s に(x−y，x−y＋Δx)に存在する確率 Ps(x−y)Δx との積事象で与えられるはずです。 ただし，最初の t 秒後の位置 y は X軸上のどこを経由してもいいので，y　について区間(-∞，∞)で積分してやった，

Ps(x−y)Pt(y)dy ・Δx　

が時刻 ｔ＋s に 微小範囲 (x，x＋Δx)に粒子がある確率となります。そしてこれら２つを等しいとし，

Pｔ+s( x )Δx＝ Ps(x−y)Pt(y)dyΔx　

とすることができます。両辺を Δxで除し，記号を改めれば，

z( x ) ＝ h(x−u)g(u)du　

と一般化して書くことできます。ここで，z(x) ，g(x)，h(x) は，それぞれ t＋s 秒後， t 秒後， s 秒後の確率分布という物理的な意味を持たせることができ，
t＋s 秒後の確率分布を， t 秒後， s 秒後の確率分布から計算して得る方法を示していると考えることができます。

こちらも参照して下さい　⇒　確率変数の和[#]

［２］ このような物理的な背景のもとで，次のような定義が行なわれます。

定義：　たたみ込み

絶対可積分関数 h(x)，g(x) にたいして次の積分値を

1
2π
h(x−u)g(u)du　≡　h(x)*g(x)           定義　I
または，
h(x−u)g(u)du　≡　h(x)*g(x) 　　　　　　　　　定義　II  
を畳み込み，または，コンボルーションと言います。



３．






２．たたみ込みの定理

I　たたみ込みの定理　　

h(x)，g(x) について，たたみ込みが，定義できるとき，

(１) たたみ込みのフーリエ変換は，各関数のフーリエ変換の積に等しい，すなわち，

F [ h(x)*g(x)] ＝ F [h(x)]・F [g(x)]
逆に，

(２) f，g が区分的に連続で，(f*g)が点 x で連続なら，
h(x)*g(x) ＝ F -1 ｛F [ h(x)]・F [ g(x)] ｝
がなりたつ。

用途に応じて，次のようにも書かれます。

II　たたみ込みの定理　( 空間  ⇔  運動量 )
u(x)＝ h(q)r(x−q)dq　　　(　≡　h*v (x)　)　
ただし， h(x)dx ＝ 1　　

なる関係があり，u(x)，r(x)，h(x) のフーリエ変換を U(k)，R(k)，H(k)，すなわち，

U(k)＝ u(x)e-i kxdx　
R(k)＝ r(x)e-i kxdx　
H(k)＝ h(x)e-i kxdx　

とすれば，

U(k) ＝ H(k)R(k)

がなりたつ。

III  たたみ込みの定理   ( 時間  ⇔  周波数 )
y(t)＝ h(τ)x(t−τ)dτ　　　(　≡　h*x (ｔ)　)　
ただし， h(t)dt ＝ 1　　
なる関係があり，y(t)，x(t)，h(t) のフーリエ変換を Y(ω)，X(ω)，H(ω)，すなわち，
Y(ω)＝ y(t)e-i ωtdt　
X(ω)＝ x(t)e-i ωtdt　
H(ω)＝ h(t)e-i ωtdt　
とすれば，
Y(ω) ＝ H(ω)X(ω)
がなりたつ。

(１) の証明：

F [h(x)*g(x)] ＝
1
2π
1
2π
h(x−y)g(y)dy e-ikxdx
＝
1
2π
g(y) e-iky・e-ik(x-y)h(x−y)dydx

r ＝ x−y として，

＝
1
2π
g(y) e-ikydy
1
2π
h(r)e-ikrdr
＝F [g(x)]・F [h(x)]
＝G(k)・H(k)　　　　　　(g(x)，h(x)のフーリエ変換をG(k)，H(k)として。)

このフーリエ変換は，

f(x)*g(x)＝F -1｛F [ h(k) ]F [ g(k) ]｝ ＝
1
2π
F [(x)]F [g(x)] eikxdx


［目次へ］