| 2 多次元確率分布 | |
| f-denshi.com 最終更新日:11/06/02 | |
| サイト検索 | |
[1] 複数個の確率変数から多次元の確率変数を作り出すことを考えよう。例えば,どの面も等確率で現れる正四面体のサイコロと立方体のサイコロの2つを同時に振って,正四面体の出目がx,かつ,立方体の出目がyとなることを,ベクトル成分として,
| X = | X | [2次元確率変数], x = | x | [2次元事象] | ||||
| Y | y |
と書くこととし,これを2次元確率変数と定義する。たてベクトルで定義するが,スペースの都合上,よこベクトルで,
tx = (x,y)
とも書く。しかし,今後用いることになる行列の混じった計算式の中では,x はたてベクトルであることを思い出す必要がある。
確率関数は,
P(X=x,Y=y)=P(X =x)
のように書いて拡張される。これを同時確率関数と呼ぶ。(離散確率変数のときは同時(確率)密度関数f(x)=f(x,y) でもある。) 2種のサイコロの出目で定義される2次元確率変数X の取り得る値(根源事象)は次のとおりとなる。(スペースの都合上よこベクトルで書く)
(1,1) , (2,1) , (3,1) , (4,1)
(1,2) , (2,2) , (3,2) , (4,2)
(1,3) , (2,3) , (3,3) , (4,3)
(1,4) , (2,4) , (3,4) , (4,4)
(1,5) , (2,5) , (3,5) , (4,5)
(1,6) , (2,6) , (3,6) , (4,6)
サイコロが均質であれば,これら24通りの出目が等確率で起こり,これらすべて,P(X=x)=1/24であるとしてよいだろう。この同時確率(密度)関数を図示すると次のように書くことができる。(赤い点以外のところではP(X =x)=0)
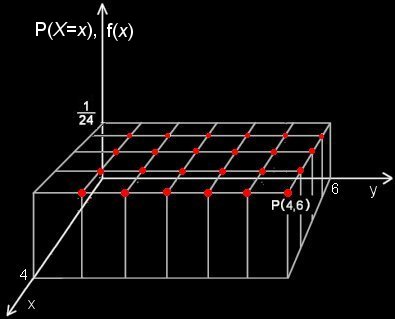
[2] ここで,どちらか一方の確率変数の値を固定した,
| P(X=x)= | P(X=x,Y=y) =f1(x) ← Xはxであるが,Yは何でもよい |
| P(Y=y)= | P(X=x,Y=y) =f2(y) ← Yはyであるが,Xは何でもよい |
をX,またはYの周辺確率(密度)関数と呼ぶ。P(Y=y)を定義に従って計算すると,
P(Y=y)=P(1,y)+P(2,y)+P(3,y)+P(4,y)=4/24
(y=1,2,3,4,5,6のとき)
P(Y=y)=0 (y=1,2,3,4,5,6以外のとき)
↑これは自明なので考えなくてもよい
であり,P(Y=y)=1/6 (y=1,2,3,4,5,6) となっているが,これは,正4面体サイコロの出目を無視し,正6面体のサイコロの出目だけをだけを考えることに等しい。
一方,2次元の累積分布関数は,
F(x,y)=P(X≦x)=P(X≦x,Y≦y)
と定義され,同時分布関数とも呼ばれる。同時密度関数とは,
F(x,y)= f(xi,yj) [離散]
という関係がある。さらに,
F1(x)=F(x,∞)=P(X≦x)
F2(y)=F(∞,y)=P(Y≦y)
をそれぞれ,X,またはYの周辺分布関数という。
問題: 同時分布関数を図示(イメージ)せよ。
[3] 多次元確率変数が連続である場合も離散的な場合と同様に次の定義を導入することができる。
2次元の同時分布関数F(x,y)は,
F(x,y)=P(X≦x)=P(X≦x,Y≦y)
とすればよい。同時確率密度関数f(x,y)との関係は,
F(x,y)= f(x,y)dydx [連続確率変数]
( f(x,y)=0,x,y<0 であれば,積分範囲は,x,y>0で行えばよい。)
および,
f(x,y) = ∂2 F(x,y) ∂x∂y
である。周辺密度関数fi(x)は,
f1(x)= f(x,y)dy
f2(y)= f(x,y)dx
となる。
[4] 実は,ここまで考えてきた2つのサイコロの出目については,暗黙の了解として,お互いにその出目に影響を及ぼし合わないとして確率を計算をしてきた。このように2つ(以上)の確率変数の間の関係がないことを2つの確率変数X,Yが独立であるいい,数学的には次のように定義する。
|
確率変数X,Yが任意の事象に対して, P(X=x,Y=y)=P(X=x)P(Y=y) [離散]あるいは確率密度について, f(x,y)=f1(x)f2(y) [離散または連続] が成り立つとき,XとYは独立であるという。 |
先程の2種類のサイコロの例(離散変数)で,出目の組が(1,3)となる確率がP(X=1,Y=3)=1/24となる根拠は,正四面体サイコロが1,かつ立方体サイコロが3となる確率を,
P(X=1)P(Y=3)=(1/4)・(1/6)= 1/24 =P(X=1,Y=3)
のように計算にしており,このような計算方法を正当化するために独立という概念が用意されている。
[5] 独立でないときは,条件付確率関数,
P(X=x|Y=y)≡ P(X=x,Y=y) P(Y=y)
を用いなければならない。ここで,記号:P(X=x|Y=y) とは,Y=y が実現している条件の下で,X=x となる確率を意味する。上式を変形して,
P(X=x,Y=y)=P(Y=y)P(X=x|Y=y)
とすれば,確率変数X,Yが独立ということは,
P(X=x|Y=y)=P(X=x) [X,Y独立]
と言い直すこともできる。
連続確率変数のときは条件付確率密度関数は,
f1(x|y)≡ f(x,y) ⇔ f(x,y)=f1(x|y)f2(y) f2(y)
と定義する。離散的確率変数の場合と同様に,確率変数X,Yが独立ということは,
f1(x|y)=f1(x)
と書けることとしてもよい。
以上まとめると,
| *名称・記号 | 離散 | 連続 | ||||||||||||||||
| 同時分布関数 F(x,y) |
|
|
||||||||||||||||
| 周辺分布関数 Fi |
|
|
||||||||||||||||
| 同時確率(密度)関数 f(x,y) |
P(X=x,Y=y)=f(x,y) または,P(X=xi,Y=yj)=f(xi,yj) |
|
||||||||||||||||
| 周辺確率(密度)関数 fi |
|
|
||||||||||||||||
| 条件付確率(密度)関数 fi(x|y) |
|
|
* 同時確率関数を同時分布,他にも周辺確率密度関数を周辺密度関数と呼ぶ人もいるなど,やや,この辺の用語は統一されていない。
[6] 以上の話のn次元確率変数への拡張は難しくないので詳述はしない。
[1] 次に独立な確率変数のX,Yから,その和,
Z=X+Y
を新たな確率変数Zとして定義することを考える。先程までは,各サイコロの出目をベクトルの各成分とみなしたが,今度はその和を一つの数に対応させることを考える。すると,先の24とおりのx=(x,y) に対して,x+y は,
| (x,y) | ⇒ | x+y |
| (1,6) , (2,6) , (3,6) , (4,6) (1,5) , (2,5) , (3,5) , (4,5) (1,4) , (2,4) , (3,4) , (4,4) (1,3) , (2,3) , (3,3) , (4,3) (1,2) , (2,2) , (3,2) , (4,2) (1,1) , (2,1) , (3,1) , (4,1) |
7 , 8 , 9 , 10 6 , 7 , 8 , 9 5 , 6 , 7 , 8 4 , 5 , 6 , 7 3 , 4 , 5 , 6 2 , 3 , 4 , 5 |
となり,これらが等確率で起きることとなる。すると,Z={z|2,3,4,5,6,7,8,9,10} の確率(密度)関数,P(Z=z)=P(X+Y=z) が,
P(Z=2)=1/24, P(Z=3)=2/24, P(Z=4)=3/24, P(Z=5)=4/24, P(Z=6)=4/24
P(Z=7)=4/24, P(Z=8)=3/24, P(Z=9)=2/24, P(Z=10)=1/24
で与えられることにすると,上の一覧と辻褄が合う。(←正四面体,立方体のサイコロが共に対称で均一ならば,このようになると信じても文句はあるまい。) 確率変数X,Yについては,確率関数P(X=x),P(Y=y)はそれぞれ一定値,1/4,および,1/6をとる定数関数(やや不正確な言い方だが)であるが,その和Zについて,P(Z=z)はもはや一定の値を返してこない。確率変数が単なる変数ではない所以である。
以上のことを,正4面体サイコロについて,P(X=x)=1/4,正6面体サイコロについて,P(Y=y)=1/6であることに注意して,図に表わすと次のとおりとなる。↓緑の点が確率関数がとる値。
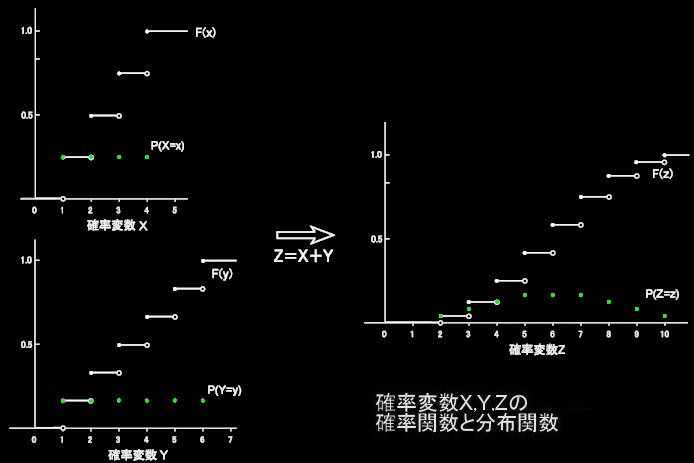
[2] 次に,これらを一般化したいのだが,まず,サイコロの目の和が4となる確率について,
P(Z=4)= P(X=x,Y=y)δ(x+y=4)
= P(X=x) P(Y=y)δ(x+y=4)
= P(X=4-y) P(Y=y) ( = P(X=x)P(Y=4-x) )
=P(X=3)P(Y=1)+P(X=2)P(Y=2)+P(X=1)P(Y=3)+ P(X=0)P(Y=4)+P(X=-1)P(Y=5)+P(X=-2)P(Y=6)
= 1 ・ 1 + 1 ・ 1 + 1 ・ 1
+0・ 1 +0・ 1
+0・ 1 6 6 6 4 6 4 6 4 6
= 3 24
(ただし,クロネッカーのデルタ:δ(z=x+y) は,z=x+y を満たすときに1,そうでないときには0をとる。また,Σは添え文字x,yのあらゆる事象について和をとる。)
のように書けることを確認しておく。
[3] すると,これを Z=z と一般化した場合では,確率関数の代わりに確率密度関数の記号で,P(X=x)→f1(x),P(Y=y)→f2(y)を用いて書くと,
f(z)= f1(x)f2(y)δ(z=x+y)
= f1(z-y)f2(y)= f1(x)f2(z-x) X,Yが独立なとき
と書いてよい。(この辺は理系学部3年生くらいの読者を想定した説明となっている。)
これは連続変数の場合にも拡張され,Xの確率密度関数をf1(x),Yの確率密度関数をf2(y)とするとき,
f(z)= f1(x)f2(y)δ(z-(x+y))dxdy
= f1(z-y)f2(y)dy = f1(x)f2(z−x)dx X,Yが独立なとき
とできる。ここで,ディラックのδ関数の性質[#],
g(x)δ(x-a)dx = g(a)
を用いた。(xで積分するときは,δ(x-(z-y)),として,yで積分するときは,δ(y-(z-x))として,δ関数の性質適用せよ。)
[4] さらに確率変数の数nを一般化した確率分布の和 Z=X1+・・・+Xn の場合,z=x1+・・・+xn として,Zの確率密度関数は,
f(z)= ・・・ f(x1,x2,・・・,xn)δ(z-(x1+x2+・・・+xn))dx1dx2・・・dxn
= ・・・ f(z-(x2+・・・+xn),x2,・・・,xn)dx2・・・dxn ・・・・[*]
となる。この表式では確率変数X1,・・・,Xnが独立でなくともよいが,確率変数Xiが互いに独立であるならばさらに,
f(z)= ・・・ f1(z-(x2+・・・+xn))f2(x2)・・・fn(xn)dx2・・・dxn
のようなn個の1変数関数の積の積分に分解されることは確率変数の数が2個の場合と同じである。これを分布関数f1(x1),・・・,fn(xn)のたたみ込みと呼ぶ。特に,n=2であるならば,
f(z)= f1(z−x2)f2(x2)dx2 n=2のたたみ込み
となり,先程の独立な2つの確率変数の和のたたみ込みを再確認できる。なお,断ってないが,±∞で密度関数は0に近づくものとしている。また,収束条件など細かいことは,とりあえずここでは気にしないでおく。
[5] 一方,(多次元(累積))分布関数F(z)については,
F(z)= ・・・ z-(x2+・・・+xn) f(x1,・・・,xn)dx1・・・dxn -∞
= ・・・ dx2・・・dxn z-(x2+・・・+xn) f(x1,・・・,xn)dx1 -∞
とすればよいことは,これをzで微分すれば,[*]となることからわかる。また,分布関数を次のように表記することもあるが,同じ意味である。
| P(Z≦z)=P(X1+・・・+Xn≦z)= | f(x1,・・・,xn)dx1・・・dxn | |
| x1+・・・+xn≦z |
これらの式においても,確率変数が独立であれば,f(x1,x2,・・・,xn) ⇒ f1(x1)f2(x2)・・・fn(xn) とできることは言うまでもない。
これは結果だけまとめておく。
| Z= | f(z) | f(z) X,Yが独立 | ||||||||
| X+Y |
|
|
||||||||
| X−Y |
|
|
||||||||
| XY |
|
|
||||||||
| X/Y |
|
|
||||||||
説明は省略する。あしからず。