
 |
6 コーシーの積分定理 | |
| f-denshi.com [目次へ]最終更新日: | ||
| サイト検索 | ||
[1] 複素積分において,
(1) 積分経路 ⇒ 単一閉曲線 C
(2) f(z) ⇒ C とその内部 D で正則関数
という条件を満たすとき,積分の値は常に 0 になるという重要な定理があります。
[2] 複素関数とその閉じた経路上の定積分を成分(実関数)に分けて,
f: z =x+i y → w =f(z) =u(x,y)+i v(x,y)
f(z)dz= (udx−vdy)+i (vdx+udy)
と書くことにします[#]。正則ならば,実数関数である:u(x,y),v(x,y)は微分可能で1階導関数が存在します。すると,グリーンの定理を用いて[#],
f(z)dz= − ∂v − ∂u dxdy +i ∂u − ∂v dxdy ∂x ∂y ∂x ∂y
と線積分を面積分に変換できます。ところが,D上で正則な関数は,コーシー・リーマンの関係式,
∂u(x,y) = ∂v(x,y) ,および, − ∂u(x,y) = ∂v(x,y) ∂x ∂y ∂y ∂x
が成り立っているので面積分の中身は常に実部,虚部ともに 0 です。すなわち,D上の積分も 0 です。
[3] きちんとこれを述べると,
| コーシー(Cauchy)の積分定理 単一閉曲線 C とその曲線が囲む領域Dにおいて関数f(z)が正則ならば, である。 |
一方,ここで述べたことの逆命題として次の定理も紹介しておきましょう
| Moreraの定理 領域 D 内の任意の単一閉曲線 C について,連続関数f(z)が, を満たすならば,f(z)は正則である。 |
証明⇒ PDFをご覧ください。
[1] コーシー積分定理から直ちに次の定理が得られます。
| コーシーの積分定理の系 領域D (開円板)において関数f(z) が正則ならば,領域内の任意の2点a,b を結ぶ曲線に沿った積分の値 は途中の経路によらず,a,b だけで決まる。 |
[証明] 右図のような積分経路を考えます。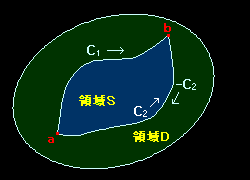
C1 : a → b
C2 : a → b
- C2 : b → a
ここでC1,C2 の曲線の形は自由ですが,経路:C=C1−C2 は a から b を経由してa に戻る単一閉曲線になるものとします。このとき,コーシーの積分定理が適用できて,
f(z)dz= f(z)dz+ f(z)dz=0
となりますが,
f(z)dz=− f(z)dz= f(z)dz
これは,a からb の積分は途中の経路によらないことを示しています。
また,この積分の起点aを固定し,bを任意のD内の任意の点zとすれば,この積分はzのみの関数であり,F(z)と書いても構わないことが分かります。
[2] この定理 + (細かい注意) を用いると,正則な f(z) について実数関数と同様な次の命題が成立することが示されます。
| (1) | f(ζ)dζ=F(z) は,zの正則関数で,F'(z)=f(z) (証明必要) | |
(2) ある F(z) が存在して,F'(z) = f(z) であるならば,(定)積分は
| ⇒ | f(z)dz=F(b)−F(a) | |
つまり,実数と同じように原始関数と呼ばれる F(z) を(定)積分に持ち込めます。 これが前ページの f(z) = z2 のインチキ積分[#] が成立する理由の半分です。
[3] 残り半分は z をなぜ実数のようにあつかって構わないかいうことですが,また後で ⇒ 一致の定理をみよ。