
 |
5 複素関数の積分 | |
| f-denshi.com [目次へ]最終更新日: | ||
| サイト検索 | ||
[1] 複素関数: w=f(z) の定積分は複素平面上の線積分 [#] として定義 されます。したがって,積分範囲(経路)は始点・終点だけでなくそれを結ぶ経路(曲線)を指定する必要があります。これはもちろん,実数が一次元の数直線上の点の集合であるのに対して,複素数が2次元のガウス平面上の点の集合であるために始点と終点を結ぶ方法に自由度が生じるためです。
[2] 複素関数の定積分の定義です。
|
この複素関数の積分を(2次元)ベクトル値関数の線積分 [#]と比較すると,
A (r) ⇔ f(z)
dr ⇔ dz
という対応関係を見出すことができます。しかしながら,この定義のままではいかにも形式的で役立ちません。
[3] 複素関数の積分は実ベクトルの線積分に対応することは,次のように複素数を成分に分けて計算することでよりはっきりしてきます。
曲線C上の点: z = x+i y
その点でのf(z)の値: w = u(x,y)+i v(x,y)
とします。このとき,
Δxk =x(tk)−x(tk-1)
Δyk =y(tk)−y(tk-1)
と書けば,先ほどの定積分は,
f(z(Tk)){z(tk)−z(tk-1)}
= {u(x(Tk),y(Tk))+i v(x(Tk),y(Tk))}{Δxk+i Δyk}
= {u(x(Tk),y(Tk))Δxk−v(x(Tk),y(Tk))Δyk}
+i {v(x(Tk),y(Tk))Δxk+u(x(Tk),y(Tk))Δyk}
この極限を,
複素関数の積分の定義 1
|
と書きます。
パラメータ t の積分として表す方法として,(Δxk/Δtk)Δtk, および,(Δyk/Δtk)Δtk を h→0 で (dx/dt)dt,および,(dy/dt)dt と書き,
複素関数の積分の定義 2
|
と書くこともできます。
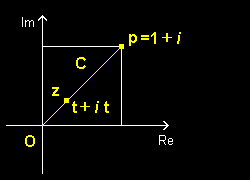 [4] 実際に積分を実行して見たほうが複素関数の積分の意味がつかめると思います。
[4] 実際に積分を実行して見たほうが複素関数の積分の意味がつかめると思います。
(1) f(z) = z2 を右のような積分経路 C (直線OP)に沿って積分します。
経路上の点 z は,媒介パラメータ t, 0≦t≦1
を用いて,
z = x+i y = (1+i )t
dz = (1+i )dt
この経路上での関数は,
z2 = {(1+i )t}2
とあらわせるので,
z2 dz= {(1+i )t}2・(1+i )dt
=(1+i )3 t 2dt
= 1 (1+i )3 3
[5] ところで,上の複素積分をこれが ”線積分” であることを無視して,あたかも z が実数であるかのように形式的に定積分を次のように実行してみると,
(1+i ) z2 dz = 1 z3 (1+i ) = 1 (1+i )3 0 3 0 3
となって,これはホントはインチキなのに答えが先ほどと同じです。つまり,定義では複素数の積分は曲線に沿った線積分で途中の経路にその値が依存するはずだったのに,この例では始点と終点の値だけで積分値が計算できてるのです。実は,このような結果になったのはこの関数 f(z)=z2 に固有の偶然ではなく,正則関数(微分可能)であれば,どんな関数についてもこのような(積分)計算が許されるのです。このことについては次ページで改めて考えることになります。
[6] もうひとつ例(演習問題)を挙げておきます。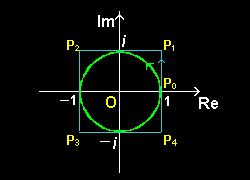
f(z)dz : f(z)= 1 ; z = x+i y ⇔ z* = x-i y z*
積分範囲C は次の2とおりで,
(1)C=C1: 単位円周上1周
(2)C=C2: 単位正方形?上1周
右に積分範囲を書いておきます。
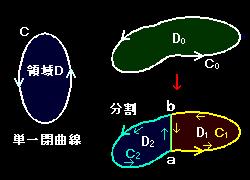 [1] 複素平面上の積分経路として,もっとも重要な曲線は,始点と終点が等しく途中で交わることのない閉じた曲線で単一閉曲線,またはジョルダン閉曲線と呼ばれます。右図の楕円形の領域D の縁(フチ)は単一閉曲線の例です。閉曲線にそって積分を行う場合,時計廻り,反時計廻りの2方向を考えられますが,反時計廻りを正方向と定め,Cまたは∂Dと書き,その逆方向を -C (-∂D)と書くことにします。線積分の性質からすぐにわかることとして,
[1] 複素平面上の積分経路として,もっとも重要な曲線は,始点と終点が等しく途中で交わることのない閉じた曲線で単一閉曲線,またはジョルダン閉曲線と呼ばれます。右図の楕円形の領域D の縁(フチ)は単一閉曲線の例です。閉曲線にそって積分を行う場合,時計廻り,反時計廻りの2方向を考えられますが,反時計廻りを正方向と定め,Cまたは∂Dと書き,その逆方向を -C (-∂D)と書くことにします。線積分の性質からすぐにわかることとして,
(1) =−
その他にも複素積分のテクニックとしてよく使われる積分経路の分割と連結について述べておきます。
[2] 正味の積分経路を不変なままにして,積分経路を分割して考察することがあります。どういうことかといいますと,右図の領域 D0 はその境界C0 上の異なる2点を結ぶ線分 ab によって,D1,D2 という2つの領域に分けられます。ここで,それぞれの領域を囲む2つの単一閉曲線の和を考えると,C1,C2 の共通部分である線分 ab 上の積分は方向が反対なのでキャンセルし合って,
(2) = +
であることがわかります。
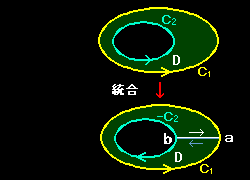 [3] 一方,領域に穴があいている場合(右図)はこの領域 D の境界は2つの閉曲線 C1と C2 とから成り立っていますが,これを1本の単一閉曲線とみなすこともできます。それは,C1とC2上の各一点を結ぶ右図のような線分 ab を付け加えて考えればよいのです。すなわち,領域D
を囲むジョルダン曲線として,まず,a から出発してC1 を正方向に一周してaへ戻り,そこから線分をたどってb にゆき,次に C2 を負の方向に(これを -C2 と書きます)一周してb に戻ってきます。そして再び線分を b から a に進み,出発点である
a に戻ってきます。すると,線分 ab 上の積分はキャンセルし合って 0 となることから。次の関係が成り立ちます。
[3] 一方,領域に穴があいている場合(右図)はこの領域 D の境界は2つの閉曲線 C1と C2 とから成り立っていますが,これを1本の単一閉曲線とみなすこともできます。それは,C1とC2上の各一点を結ぶ右図のような線分 ab を付け加えて考えればよいのです。すなわち,領域D
を囲むジョルダン曲線として,まず,a から出発してC1 を正方向に一周してaへ戻り,そこから線分をたどってb にゆき,次に C2 を負の方向に(これを -C2 と書きます)一周してb に戻ってきます。そして再び線分を b から a に進み,出発点である
a に戻ってきます。すると,線分 ab 上の積分はキャンセルし合って 0 となることから。次の関係が成り立ちます。
(3) = −
このような穴が幾つ(有限個)あっても,同様な議論が可能なことは言うまでもありません。
[4] 最後に積分の計算でよく使う評価式を挙げておきましょう。
| (1) | |dz| = (曲線Cの長さL ) |
(2) 曲線 C上で f(z)≦g(z) ならば,
|f(z)||dz| ≦ |g(z)||dz|
(3) 長さL の曲線C を含む領域で複素関数 f(z) は連続で,C上で|f(z)|≦M とするとき,
f(z)dz ≦ |f(z)||dz|≦ ML
等号が成り立つのは C上で常に|f(z)|=M がなりたつとき,すなわち,定数関数のときのみです。