|
1 複素数とガウス平面 | |
| f-denshi.com ［目次へ］最終更新日：08/02/07 | ||
| サイト検索 | ||
［1］ 複素数のちょっと高級な定義から始めましょう。
|
［複素数：ハミルトンの定義］ 複素数とは２つ実数の組で，次の演算規則をみたすものである。 |
減法，除法はそれぞれ，加法，乗法の逆演算として定義します。もちろん，高校生の時に習った複素数の演算規則はこれらを満足しています。
［２］ 高校レベルの定義の方が直感的には分かりやすいので書いておきましょう。複素数 z＝(x,y)を，
z ＝ x+yi ， x，y ∈ R (実数) (ただし， i 2＝−1)，
と書ける数とします。i を虚数単位といい，x を実数部，y を虚数部といい，このことを
Re(z)＝x， Im(z)＝y
のように書きます。また，Re(z)＝0，Im(z)≠0 なる複素数を純虚数といいます。 一方，Im(z)＝0 なる複素数は実数です。つまり，集合として， 実数 ⊂ 複素数。
［３］ ここまで，プラス記号が色分けされてたことにはワケがあります。＋(複素数の足し算)，+(実数の足し算)，+(複素数の実数，虚数成分を仕切るカンマの代わり？)という意味の違いがあることに気づいたでしょうか？数学は厳密性をウリにする学問ですが一つの記号をいろんな意味に実によく混同して使います[#]。そこには歴史的な経緯や区別する価値が少ない場合もあるのでしょうが，しばしば初学者の理解の妨げにもつながる困ったことです。しかし，この講義でしか通用しない記号を次々定義しては逆にヒンシュクを買いかねないので慣用に従い，これ以後，この３つとも同じ色の記号＋を使用することにします。複素数のかけ算についても実数の掛け算の演算記号と混同が起こっていますが，ともに乗法記号「 ･ 」を使います。ただし，乗法記号はしばしば省略されます。
［４］ 複素数を z＝x＋yi ，とするとき，x−yi を共役複素数といい，
z*＝x−yi または，
z と書きます。 ←こっちの表記が一般的ですが，WEB上のときわ台学では z* を使います。
このとき次の性質があります。
(1) Re(z)＝(z＋z*)/2 ； Im(z)＝(z−z*)/2i
(２) (z1＋z2)*＝z1*＋z2*
(３) (z1z2)* ＝z1*z2*
(４) z＝ z* ⇔ zは実数
z＝-z* ⇔ zは純虚数 (z≠0)
(５) zz*≧0
証明は簡単なのでパス。
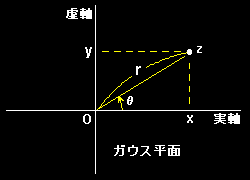［1］ 複素数が実数の ”組” であることから，これを二次元平面上の点で表現することもできます。この平面を複素平面，もしくはガウス平面といいます。横軸は実数軸，たて軸は虚数軸とすると，複素数 z＝x+yi ＝(x,y) はこの平面上の実数成分＝x， 虚数成分＝y とする平面上の１点で表現できます。(右図)
［２］ ２次元ユークリッド平面上の点が極座標でも表されるのと同様な流儀で，ガウス平面上の複素数を極座標でつぎのように表すこともできます；
z＝r(cosθ＋i sinθ) ･･･････ [*]
ここでの２つの独立変数 r，θを動径，偏角と呼び，zと次のような関係にあります。
動径 ｜z｜＝r (＝(x2+y2)1/2)
偏角 arg z＝θ＋2πm (tanθ＝y/x ) ； m：整数
θの定義域を［-π，π)などと制限すると z に対してθが一意的に決まります。しかし，複素関数解析ではθを制限しないで考えることが普通です。 複素関数は多価関数であることが本質的に有用だからです。 ⇒[#]
［３］ ガウス平面の単位円上の点，つまり，動径 r＝1 の複素数： cosθ＋i sinθ を
| cosθ＋i sinθ≡ｅi θ (またはexp(i θ)) [オイラーの関係式] |
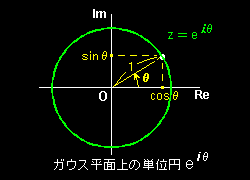と表します。この表記をオイラーの関係式（またはオイラーの公式）といいます。あたかも指数関数のような記号を用いています(実数の指数関数と同じ記号を使用する意図的混同がなされています)が，実数の場合のようにネイピア数を底とする指数関数が解析的な(極限として)定義されてるわけではありません。その定義は次のようです。
実数の場合の指数関数のマクローリン展開，
ｅθ＝1＋ 1 θ＋ 1 θ2＋ 1 θ3＋･･･＋ 1 θn ･･･ 1！ 2！ 3！ n！
の右辺において，機械的に(数学的な意味づけなしに) θ → i θ とした次式，
|
を ｅiθ の定義とします。右辺が収束するかしないかは別に検討[#]が必要ですが，その無限級数（＝ガウス平面上の点列です）の意味ははっきりしていますね。(1)の右辺が収束するならば，実数成分，虚数成分もそれぞれにおいて収束するはずです。そこで，余弦関数，正弦関数の級数展開が，
cosθ＝1− 1 θ2＋ 1 θ4− 1 θ6＋･･･ 2！ 4！ 6！
sinθ＝θ− 1 θ3＋ 1 θ5− 1 θ7＋･･･ 3！ 5！ 7！
であることを思い出せば，(1)の右辺の無限級数は，
cosθ＋i sinθ
に等しいことがわかります。これがオイラーの関係式です。複素数の微分の定義など一切使っていませんね。この関係式を用いると，任意の複素数 z の極座標表示[*]は rｅiθ とも書くことができます。また，上の級数展開を用いた表記に戻って，
ｅiθ1･ｅiθ2＝ｅi (θ1＋θ2)
を確かめることもできます。このような無限級数を介しての複素関数(正確には微分可能な関数である正則関数)の定義は複素関数論の常套手段です。
［４］ 最後に複素数の演算，すなわち，加法と乗法の幾何学的な意味を考えて見ましょう。
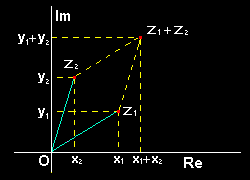(1)加法
複素数の加法は複素数をガウス平面上(直交座標)で表した２次元ベクトルとみなし，そのベクトルどうしの和と見なすことができます。
z1＋z2＝(x1＋y1i )＋(x2＋y2i )
＝(x1＋x2)＋(y1＋y2)i
減法は引くべきベクトルの向きを180°反転させたベクトルを加えることになります。
(２)乗法
複素数の乗法は複素数をガウス平面上でベクトルを極座標系で表し，その動径についてはかけ算，偏角については足し算を行うことになります。
なぜなら，r1ｅiθ1 と r2ｅiθ2 とのかけ算は，
z1z2＝(r1ｅiθ1)(r2ｅiθ2)
＝(r1r2)ｅi (θ1＋θ2)
この様子をガウス平面上に幾何学的に図示すると， ( O，1，z1) の３点を頂点とする三角形を r2 だけ相似拡大(または縮小)し，次にその相似な三角形をOの周りに θ2 だけ正方向に回転させたときの頂点 z1 に対応する点 z1z2 となります。
特にある数 z に対して，
「ｅiθ をかけることは z を原点の周りに θ 回転させる」
ことに相当します。
