| 丂丂Apendix 2丂儐乕僋儕僢僪偺屳彍朄 | ||
| f-denshi.com 嵟廔峏怴擔丗 *** | ||
| 乵栚師傊乶 | ||
乵侾乶丂嵟戝岞栺悢偺掕媊偱偡丅
惍悢丂a丄d丂偑偁偨偊傜傟偰丄
a亖d丒q 偲側傞傛偆側惍悢q丂偑懚嵼偡傞偲偒丄d 傪 a 偺栺悢丄偁傞偄偼 a 偼 d 偺攞悢偱偁傞偲偄偄傑偡丅 b亖d丒q乫 偲側傞q乫偑懚嵼偡傞偲偒丄d 偼 a 偲 b 偺岞栺悢偱偁傞偲偄偄傑偡丅 乮a丄b乯 偲彂偒傑偡丅 |
乵侾乶丂嵟戝岞栺悢傪媮傔傞傾儖僑儕僘儉偼埲壓偺偲偍傝偱偡丅
| 儐乕僋儕僢僪偺屳彍朄
惓惍悢a丄b乮a亜b乯偑梌偊傜傟偨偲偒丄埲壓偺曽朄偱嵟戝岞栺悢偑媮傔傜傟傞丅 乵戞侽僗僥僢僾乶丂 乵戞侾僗僥僢僾乶丂 丂丂丂丂丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒 乵戞倠僗僥僢僾乶丂 丂丂偙傟傪孞傝曉偡偲丄倰0亜倰侾丒丒亜倰k丒丒丒亜0丂側偺偱丄偄偮偐昁偢丄 乵戞値僗僥僢僾乶丂 丂丂偲側傞丅偙偺偲偒丄倰n 偼 a 偲 b 偺嵟戝岞栺悢偱偁傞丅偡側傢偪丄 丂丂丂丂乮a丄b乯亖倰n 丂丂偱偁傞丅 |
乵俀乶丂徹柧偼師偺柦戣傪孞傝曉偟梡偄偰峴偄傑偡丅丂丂丂丂丂丂丂
| 柦戣丂丂丂
惓惍悢a丄b乮a亜b乯偑梌偊傜傟偨偲偒丄a傪b偱妱偭偨彜傪q丄梋傝傪倰偲偡傞丅偡側傢偪丄 丂丂丂丂丂丂a亖qb亄倰丂丂丂乮侽亝倰亙b乯 丂丂丂丂丂丂乮a丄b乯亖乮b丄倰乯丂丂丂丂丂丂 丂丂丂丂丂丂丂丂丂丂丂丂 |
徹柧
a亖qb亄倰丂丂丂丂(1)
r亖a亅qb丂丂丂丂(2)
(a丆b)亖m丆丂(b丆r)亖n丂偲偟傑偡丅
(1)傛傝丆塃曈偼n偱妱傝愗傟傞偺偱丆嵍曈a傕n偱妱傝愗傟傞丅
丂丂佀丂n偼a偲b偺岞栺悢偱丆n亝m
(2)傛傝丆塃曈偼m偱妱傝愗傟傞偺偱丆嵍曈r傕m偱傢傝愗傟傞丅
丂丂佀丂m偼r偲b偺岞栺悢偱丆m亝n
偟偨偑偭偰丆m亖n偱偁傞偙偲偑暘偐傝傑偡丅
乵俁乶丂偙偺柦戣傪儐乕僋儕僢僪偺屳彍朄偺戞侽僗僥僢僾偵揔梡偡傟偽丄
乮a丄b乯亖乮倰0丄倰1乯
戞侾僗僥僢僾丄丒丒丒丄戞値亅侾僗僥僢僾偲弴偵揔梡偡傟偽丄
乮倰0丄倰1乯亖乮倰1丄倰2乯亖丒丒丒亖乮倰n-1丄倰n乯亖倰n
偑傢偐傝傑偡丅偡側傢偪丄
乮a丄b乯亖倰n
偱偁傞偙偲偑傢偐傝傑偡丅
乵係乶丂儐乕僋儕僢僪偺屳彍朄偺僾儘僙僗傪媡偵扝傞偲丄旕忢偵廳梫側師偺掕棟傪摼傑偡丅
| 掕棟
惍悢 a丄b 偑梌偊傜傟丄a 偲 b 偺嵟戝岞栺悢傪 d 偲偡傞丅偙偺偲偒丄 Xa亄Yb亖d 傪傒偨偡惍悢 X丄Y 偑懚嵼偡傞丅 |
乮徹柧乯
儐乕僋儕僢僪偺屳彍朄偱戞侽偐傜戞乮値亅侾乯僗僥僢僾 [#] 傑偱傪曄宍偡傞偲
丂丂丂丂丂丂丂 丂丂丂倰1亖a亄q1b
丂丂丂丂丂丂丂丂丂丂丂丂丂丂伀
丂丂 丂丂丂倰2亖b亄q2倰1
丂丂丂丂丂丂丂伀
倰3丂倰1亄q3倰2
丂丂丂丂丂丂丂丂丂丂丒丒丒丒丒丒丒丒
丂丂丂丂丂丂丂丂倰n-1亖倰n-3亄qn-1倰n-2
丂丂丂丂丂丂丂丂丂丂丂伀
倰n亖倰n-2亄qn倰n-1丂丂丂
偲側傝傑偡偑丄奺幃偺塃曈傪壓偺幃偵伀弴偵戙擖偟偰倰1丄倰2丄丒丒丒倰n-1傪徚嫀偟偰偄偔偲丄
倰2 亖b亄q2乮a亄q1b乯
倰3 亖乮a亄q1b乯亄q3乮b亄q2乮a亄q1b乯乯
丂 亖乮1亄q2q3乯a亄乮q1亄q1q2亄q3乯b
丂丂丂丂丂丂丒丒丒丒丒丒丒丒
丂丂丂丂丂伀
倰n 亖乮qi 偺愊偲榓乯亊a亄乮qi 偺愊偲榓乯亊b
傪摼傑偡丅偙偙偱丆qi 偺愊偲榓偼傕偪傠傫惍悢偱偡偐傜掕棟偑徹柧偝傟偨偙偲偵側傝傑偡丅
埲忋偺峫嶡偼懡崁幃偵抲偒姺偊偰傕偦偺傑傑惉傝棫偪傑偡丅佀丂掕棟
乵俆乶丂嬶懱揑偵尒偰傒傑偟傚偆丅掕棟偵傛傞偲丄a亖182丄b亖21丂偑梌偊傜傟傞偲
嵟戝岞栺悢丂d亖7丂佀丂丂182X亄21Y亖7丂偲側傞惍悢 X丄Y 偑懚嵼偡傞
偑惉傝棫偪傑偡丅儐乕僋儕僢僪偺屳彍朄偱182偲21偺嵟戝岞栺悢傪媮傔傞夁掱偼丄
182亖8丒21亄14丂丂丂 仺丂14亖182-8丒21丂丂丒丒丒嘆
丂21亖1丒14亄7丂丂丂丂仺丂 7亖21亅1丒14丂丂丒丒丒嘇
丂14亖2丒7
偲側傝丄d亖俈偑傢偐傝傑偡丅偝傜偵丄嘆傪嘇偵戙擖偟偰丄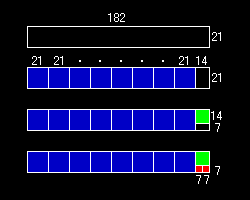
7亖21亅1丒14
丂亖21亅1丒乮182亅8丒21乯
丂亖-1丒182亄9丒21
偡側傢偪丄X亖-1丄Y亖9丂偑曽掱幃丂182X亄21Y亖7丂夝偺堦慻偲偟偰媮傑傝傑偡丅
丂偙偺僾儘僙僗偼曈偺挿偝偑182亊21偺挿曽宍傪杽傔恠偔偡惓曽宍偺偆偪偱丄堦曈偺挿偝偑嵟戝偺傕偺傪媮傔傞傾儖僑儕僘儉偲摨偠偵側偭偰偄傑偡丅塃偺恾傪嶲徠偵峫嶡偟偰偔偩偝偄丅