| 7 偏微分とCr級の関数 | ||
| f-denshi.com [目次] 最終更新日:06/04/01 | ||
| サイト検索 | ||
具体的な多変数関数が与えられ,その微分可能性を定義にしたがって確かめることは多く関数の場合で困難です。この理由は微分の定義の中に,調べようとしている「点 P にどんな近づき方をしても・・・」というくだりがあるからです。”どんな”ということはすべての可能性について調べなければならないのです。そこで実用上は,一つの方向のみ,すなわち,一つの変数以外は定数とみなす ”偏微分” と呼ばれる形式的な微分可能性とその偏導関数の連続性を用いて議論されることが多くなります。
[1] 2変数関数 f(x,y)を考えます。 次の極限値 A,
A= f(a+h,b)−f(a,b) h
が存在するとき,f(x,y)は点(a,b)において x について偏微分可能といい,A を x についての偏微分係数といい,
A ⇒ fx(a,b)= ∂f(x,y) ≡ ∂f(a,b) ∂x x=a,y=b ∂x
のように書きます。同様に,
B= f(a,b+h)−f(a,b) h
が存在するとき,f(x,y)は点(a,b)において y について偏微分可能といい,B を y についての偏微分係数といい,
B ⇒ fy(a,b)= ∂f(x,y) ≡ ∂f(a,b) ∂y x=a,y=b ∂y
のように書きます。
[2] また,f(x,y) が領域 D [#] の任意の点で,x について偏微分可能なとき,
fx = fx(x,y) = ∂f ∂x
と書き,領域 D における x についての偏導関数といいます。 y についても同様に定義します。
[3] ある関数が偏微分可能なだけでは,
(1)全微分可能な関数 とはいえない。
(2)連続関数 とはいえない。
ことに注意しましょう。 具体例→[#] をみておくのが一番です。
[4] 一変数のときと同じように2変数関数についても高階偏導関数を定義することができます。
| f(x,y): | x で偏微分 | fx(x,y) | x で偏微分 |
|
||||
| → | → |
| f(x,y): | x で偏微分 | fx(x,y) | y で偏微分 |
|
|||||||||||||
| → | → |
| f(x,y): | y で偏微分 | fy(x,y) | x で偏微分 |
|
|||||||||||||
| → | → |
| f(x,y): | y で偏微分 | fy(x,y) | y で偏微分 |
|
||||
| → | → |
ただし,一般にはfxy(a,b)≠fyx(a,b)には注意です。具体例を挙げておくと,
f(x,y)=
xy(x2−y2) : (x,y)≠(0,0) x2+y2 0 : (x,y)=(0,0)
これら関数は原点で, -1=fxy(0,0) ≠ fyx(0,0)=1 です。
[5] 偏微分係数は,x軸方向,またはy軸方向のどちらか一方向にだけに変数を変化させ,その(直線)方向に沿った関数z=f(x,y)の傾きを求めていることになります。2変数関数の定義域がxy平面であることを考えれば,直線的な変数の変化方向は,「たて,よこ」の2とおりに限定する必要はありません。そこで,x軸とθの角をなす方向に変数を変化させたときの”傾き”が次のように定義されます。
C= f(X+hcosθ,Y+hsinθ)−f(X,Y) h
この極限が存在するとき,Cを点(X,Y)における方向微分係数といいます。また, f をhの合成関数 z=f(x(h),y(h)) ,x=X+hcosθ,y=Y+hsinθとみなして[#],hで微分すると,
C= df = ∂f dx + ∂f dy dh ∂x dh ∂y dh =v ・u
= ∂f(x,y) cosθ+ ∂f(x,y) sinθ ∂x ∂y
ただし,
v = ∂f(x,y) , ∂f(x,y) ,u = cosθ,sinθ ∂x ∂y
とベクトルの内積を用いて方向微分係数を書き表すことができます。したがって,|u |=1に注意すれば,「u がv と同じ方向を向いている ( =v と同じ向きの方向微分を考える) 」とき,Cは最大値|v|をとリます。
これを言い換えると,デカルト座標に,z=f(x,y) をプロットしたとき,傾きが最大となる方向がv の方向であることを意味しています。そのため,v はf(x,y)の勾配と呼ばれます。また,形式的ですが,(2次元の)ナブラと呼ばれるベクトル,
∇≡ ∂ , ∂ ∂x ∂y
を定義して,v=∇f というようなスカラー積として書くことがあります。⇒[#]
また,
df =v ・u ⇔ df=v ・(dhu)=∇f・du dh
と表記されることもできます。
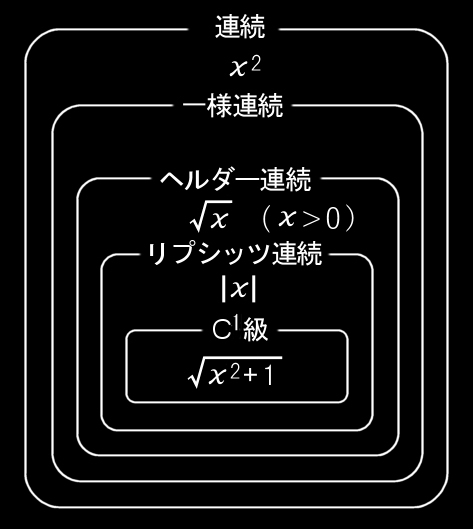
[1] 多変数関数を扱うとき,「f(x,y)を全微分可能な関数とする,・・・」と関数を指定することは必ずしも多くありません。特に応用数学では。なぜなら関数の全微分可能性の定義をそのまま具体的な証明に利用することが難しいからです。そこで,「Cr級の関数」という定義が実際の場面ではよく使われます。この概念は関数の微分可能性より厳しい条件なので,適用できる関数の範囲を制限することになります。しかし,実用上,このクラスの関数を考えれば十分な場合がほとんどです。
[C1級の関数]
領域Dで定義された関数f(x,y) がD 上で,
(1) 偏微分可能 ⇔ fx,fy が存在
(2) 偏導関数 fx,fy が連続
[C2級の関数]
2階偏導関数,
fxx,fxy,fyx,fyy
が存在して,これらすべてが連続であることが必要です。
[Cr級の関数]
これを一般化すると,
| [Cr級の関数] 領域Dで定義された関数 f(x,y) がD 上で, (1) n 階までの偏導関数がすべて存在 (2) n 階までの偏導関数がすべて連続 |
となります。
[2] [Cr級の関数 ( n > 1 ) の性質]
多変数関数がD上で,2階偏導関数をもつだけでは,一般に fxy≠fyxですが,C2級の関数ならば,fxy=fyxです。Cr級の関数 の性質のもつ特徴として一般化できます。
|
定理 fxy,fyx が存在し,それらが連続関数であれば,つまり,f(x,y)がC2級関数ならば,
同様に,C3級の関数について, などなど。 |
が成り立ちます。 証明は ⇒ [#]
[3] また,テーラーの定理の系 [#]において,
| f(x) = f(a)+ | f'(a) | (x−a)+ | f''(a) | (x−a)2+・・・+ | f(n)(a) | (x−a)n+ | f(n+1)(θ) | (x−θ)ndθ | |
| 1! | 2! | n! | n! |
と展開したとき,最後の積分項が発散してしまわないかどうか問題となります。しかし,関数 f(x) が Cn+1級であると仮定すれば,「連続関数は積分可能である。」[#] という定理を用いて,この積分項が収束することがわかります。 つまり,このテーラーの定理では,関数 f(x)が無限回微分可能ではなくてもよいのです。他にも考える関数の範囲を Cr級の関数とするような議論は変分学や解析力学でも行われます[#]。
[4] 以上,いくつか述べた関数のお互いの関係は右図のようになります。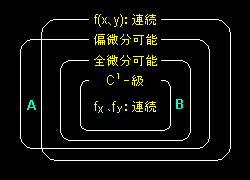
A:原点で偏微分可能だが,連続でない関数の例
f(x,y)=
xy : (x,y)≠(0,0) x2+y2 0 : (x,y)=(0,0)
B:原点で全微分可能だが,C1級ではない関数の例
f(x,y)=
(x2+y2)sin 1
x2+y2 (x,y)≠(0,0) 0 (x,y)=(0,0)
|
fxy,fyx が存在し,それらが連続関数であれば,つまり,f(x,y) が C2級関数ならば, fxy = fyx |
の証明です。
まず,2階連続微分可能な関数 f(x,y) から次の関数をつくります。
φ(x) = f(x,b+k)−f(x,b)
この微分は,
φ'(x) = fx(x,b+k)−fx(x,b)
となります。そこで,,平均値の定理を用いて次のような計算をすると,
φ(a+h)−φ(a) = hφ'(a+θh)
= h{fx(a+θh,b+k)−fx(a+θh,b)
さらに,y=b,y=b+k との区間に平均値の定理を用いて,
= hkfxy(a+θh,b+θ'k)
となります。 よって,
φ(a+h)−φ(a) = fxy(a+θh,b+θ'k) = fxy(a,b) ・・・・・(1) hk
今度は,x と y の役割を入れ換えて,
ψ(y)=f(a+h,y)−f(a,y)
を考えます。この関数について,先ほどと同様な計算を行えば,
ψ(b+k)−ψ(b) = ・・・ = fyx(a,b) ・・・・・(2) hk
が導かれます。ところが,よく見ると,
φ(a+h)−φ(a)=f(a+h,b+k)−f(a+h,b)−f(a,b+k)+f(a,b)
=ψ(b+k)−ψ(b)
なので,(1)と(2)の左辺は等しいのです。つまり,その右辺も等しく,結局,
fxy(a,b)=fyx(a,b)
であることが証明されました。
定義域 -∞≦x≦∞
f(x)=√x x≧0