
| t113 統計性の可視化 |  |
|
| f-denshi.com 更新日: 13/08/02 | ||
| サイト検索 | ||
| 目次へ | ||
フェルミ統計,ボーズ統計,古典統計を具体例を使って比較してみましょう。
状態数の数は統計性によって,
フェルミ統計 ≦ 修正古典統計 ≦ ボース統計 ≦ 古典統計
であること,1つの状態に対して,1つの粒子しか占有し得ない状況下で,
フェルミ統計 = 修正古典統計 = ボース統計
となること,がこのページでの考察で分かります。
また,粒子数が少ない状況では,修正古典統計には具体的な描像が存在せず,修正するために行う 「n!で割る」 という計算が結果オーライの場当たり的な処方であることも浮き彫りになります
[1] さっそく,前ページのグランドカノニカルアンサンブルの方法(変数:T,V,μ)に基づいて次のような固有状態をもつ仮想的な準位を考えていきましょう。(ここでは体積Vは考えません。)
エネルギー固有値は3つあり,上記のとおりとします。第1励起状態は2重に縮退,第2励起状態は3重に縮退しているとします。つまり,固有状態は合計で6個あり,同じエネルギーを持つ微視的状態を区別するためには,第2励起状態は2a,2b,および,第3励起状態は3a,3b,3cという記号も必要に応じて使います。
さて,粒子数表示で,この系の大分配関数を表すと,
Ξ= exp{-β[n1(ε−μ)+n2(2ε−μ)+n3(2ε−μ)+n4(3ε−μ)+n5(3ε−μ)+n6(3ε−μ)]}
となります。ここで,q=(n1,n2,n3,n4,n5,n6)ですが,ni はフェルミ粒子に対しては,0か1,ボース粒子に対しては,0以上のあらゆる整数について,それぞれが独立にとることができます。
分布関数は,エネルギーεjの縮退をΔj として[#],
f(εj,μ)=<nj>= Δj
+: フェルミ(-ディラック)分布関数(FD分布) 0: ボルツマン分布 −: ボース(-アインシュタイン)分布関数(EB分布) exp{(εj−μ)/kT}±1
で与えられますが,ここでは3つのエネルギー準位(j=1,2.3)の粒子占有数<nj>を化学ポテンシャルの関数とみなして,別々に見ていきます。
ここで,下添え字 「j 」 は固有状態に対してではなく,エネルギー準位に付けられた通し番号です。
もし状態に対する番号とみるならば,Δj=1 として6個のf(εj,μ)を考えることになります。
仮想3準位系に入る粒子がフェルミ粒子である場合,各エネルギー準位を占有する粒子数の期待値は次の関数で与えられます。(上の式を少し変形しただけ。)
<nε1(μ)>f= 1 [基底状態の占有数]
exp 1− μ ε +1 ε kT
<nε2(μ)>f= 2 [第1励起状態の占有数]
exp 2− μ ε +1 ε kT
<nε3(μ)>f= 3 [第2励起状態の占有数]
exp 3− μ ε +1 ε kT
ただし,
<nε1(μ)>f ≡<na>
<nε2(μ)>f ≡<nb1>+<nb2>
<nε3(μ)>f ≡<nc1>+<nc2>+<nc3>
ここで,温度を,
ε =1,および,20, ⇔ T= ε =1,および,T=0.05 ε kT k k
の2とおり選んで,各準位の占有粒子数<nj>を化学ポテンシャル(μ/εとして)の関数としてプロットすると,次のようになります。
 |
 |
|
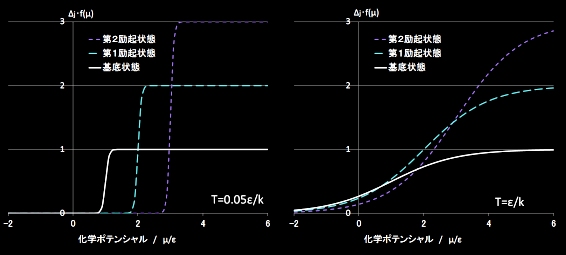
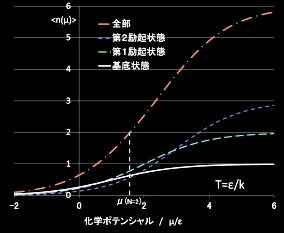
| 各エネルギー準位占有粒子数のμ依存性(フェルミ粒子) | 系の全粒子数のμ依存性(フェルミ粒子) |
T=0.05ε/kの比較的低温では,
マイナス側から化学ポテンシャルを増加させてゆくと,低いエネルギー準位から順番に,粒子占有数がほぼステップ状に増加してゆくことが分かります。化学ポテンシャルが大きい(μ=5〜6ε)ときは,各エネルギー準位の6つすべての固有状態が粒子で1ずつ満たされることが分かります。(そのときの占有数の差は状態数の差に基づく。)
化学ポテンシャル
ここで,グランドカノニカルアンサンブルで重要な役割をもつ化学ポテンシャルの意味を再確認しておくと,化学ポテンシャルとは,与えられた条件下で,系の粒子数を増減させるために必要なエネルギーです。1つの粒子を系に加えるのであれば,そのとき,系が獲得するエネルギー,逆に1つの粒子を失うのであれば,そのとき,系が失うエネルギーです。3準位系の基底状態のエネルギーはεですから熱粒子浴の化学ポテンシャルがμ=ε(以上)にあって,熱平衡にあるとき,基底状態には粒子が一つ存在できるようになるということです。ただし,絶対零度の場合を除く有限温度では熱揺らぎのために,εよりわずかに低いμにおいて,占有粒子数増加の兆しが見られ,わずかに高温の温度域で粒子数が減少しています。つまり,温度(熱)は化学ポテンシャルで定まる系の粒子数変化を鈍らせ,平均化(スムージング)する働きをするのです。励起状態に関しても基底状態同様の考察が可能です。(← 詳しくは,<nε1(T,μ=ε)>f=1/2で,<nε1(T=0,μ=ε)>fはμ=εで0から1へジャンプするステップ関数。) 化学熱力学のところでも強調しました[#]が,化学ポテンシャルとは,系の平均(ギブス自由)エネルギーの1モル当たりや1粒子当たりの値ではないのです。ここで考えている系のフェルミ粒子の増減は,系の平均的なエネルギーを持っているフェルミ粒子の増減ではなく,最も高いエネルギーを持っている粒子の増減が化学ポテンシャルに対応すると考える必要があります。)
T=ε/kの比較的高温では,
化学ポテンシャルの効果に比べて,温度の効果が無視できません。化学ポテンシャルをマイナス側から増加させていくと,μがまだ,εに達していないマイナスの領域からすべての準位に粒子が入っていくことが分かります。また,比較的低い化学ポテンシャルの領域では,低い準位ほど粒子占有率は高いのですが,化学ポテンシャルが高くなると,第1励起状態,第2励起状態の粒子占有数の上昇率が大きくなり,最終的には,<n1>:<n2>:<n3>= 1 : 2 : 3 へ漸近していくことが分かります。
厳密には,以上の考察においてμそのものの温度依存性も考える必要がありますが,話が複雑になるので,とりあえず無視しました。一番右の図は,系全体の粒子占有確率の化学ポテンシャル依存性を示しています。この図から系の平均粒子数と化学ポテンシャルの関係が分かります。つまり,トキワニウムの”酸化数(価数)”と化学ポテンシャルの関係が分かります。 ・・・・・
|
BE分布 省略 |
ボルツマン分布
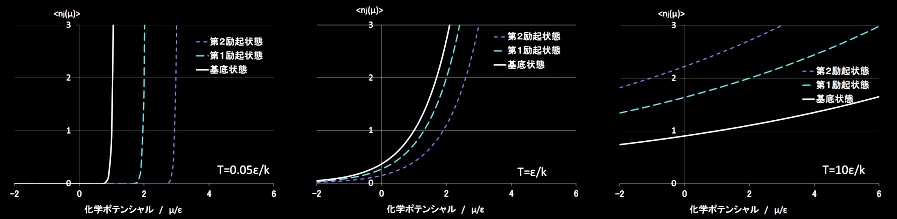 |
| 各エネルギー準位占有粒子数のμ依存性(古典粒子) |
ボルツマン分布は,フェルミ-ディラック分布とボース-アインシュタイン分布の両方の特徴を持った分布であることがわかります。低温(T=0.05ε)において化学ポテンシャルをマイナス側から増加させていくと,μ=ε,2ε,3εの付近で,基底状態,第1励起状態,第2励起状態にそれぞれ粒子が急激に入ってゆく増加関数であることはフェルミ-ディラック分布の場合と同じです。ところが,占有粒子数(確率)に制限がないため,こちらはボース-アイシュタイン分布同様にいくつでも粒子が各準位に入っていきます。温度を上昇させると,増加関数はなまされて緩やかになり,エネルギー縮退数の影響が強く表れて,占有数は基底状態<第1励起状態<第2励起状態と低温のときと逆転します。
まとめ:3準位系の基底状態の占有粒子数の化学ポテンシャル依存性についてひとつの図に表しました。
(基底状態のエネルギーをεとしていることに注意せよ!)
[1] 1.と同じトキワニウム(仮想3準位系)について,今度はミクロカノニカルアンサンブルの描像で見てみましょう。このアンサンブルの特徴は,微視的状態に等重率の原理が適用可能なことです。したがって,微視的状態を一つひとつ具体的に拾いだすとそれらはどれも対等な微視的状態として扱うことができます。
1粒子系の場合
「系のエネルギーE」 = 「1粒子エネルギー」 = 「粒子が占有するエネルギー準位εj」
となります。また,同じエネルギーεj を与える準位の数を縮退度(または状態密度に相当)と呼び,
Δ(εj)
と書きます。具体的には,
Δ(ε) = 1, Δ(2ε) = 2, Δ(3ε) = 3
となっています。また,1粒子の場合は,系がエネルギーEを持つ時の状態数Wと,
W(E,N=1)=Δ(E)
との関係があります。状態 r である確率を,pr(E)=1/W(E,N=1) と書くと,
pa(ε)=1
pb1(2ε)=pb2(2ε)=1/2
pc1(3ε)=pc2(3ε)=pc3(3ε)=1/3
となります。例えば,E=3εと指定すれば,c1,c2,c3の3つの状態が糖確率で出現します。
[2] カノニカルアンサンブルで考えるならば,6つの微視的状態(=6つの固有状態)をすべて考えることとなりますが,各微視的状態が出現する確率は,与えられた温度とボルツマン因子を用いて,
p1=e-ε/kT/Z1,
p2a=p2b=e-2ε/kT/Z1,
p3a=p3b=p3c=e-3ε/kT/Z1
となります。ここで,分配関数Z1は,
Z1= exp(-E/kT) =e-ε/kT/Z+2e-2ε/kT/Z+3e-3ε/kT
= W(E)・exp(-E/kT)
で定義されます。分配関数が求まれば,残りの熱力学量も形式的に求まりますが,これ以上書いてもおもしろくないのでやめておきます。
2粒子系の微視的状態数
[3] 2粒子系を考えると,統計性の違いが表れておもしろいことが起こります。2つの粒子の状態がそれぞれ,i,j であるとき,系の状態rを
r= [ij]
と書き,(2粒子からなる)系の微視的状態 と呼ぶことにしましょう。 単純な重複順列を考えると,この系には36個の微視的状態があり,それらは,
r = [11],[12a],[2a1], ・・・・・ ,[3c3b],[3c3c]
となります。 また,各粒子間の相互作用がないとすれば,系のエネルギーEは各粒子の持つエネルギーの和で与えられます。
たとえば,系のエネルギーがE=3εであるときの系の微視的状態数は,
r=[12a],[2a1],[12b],[2b1]
の4つなので,
W(E=3ε,N=2)=4
となります。分配関数を求めるためには,1粒子状態が独立であることから,
Z2=(Z1)2=(e-ε/kT+2e-2ε/kT+3e-3ε/kT)2
=e-2ε/kT+4e-3ε/kT+10e-4ε/kT+12e-5ε/kT+9e-6ε/kT
⇔ W(E)・exp(-E/kT)
と計算されます。ここで,各指数項の係数が,系がエネルギーEをもつときの状態数W(E,N=2)を与えています。
[4] この結果より状態数を図示すれば下のようになります。
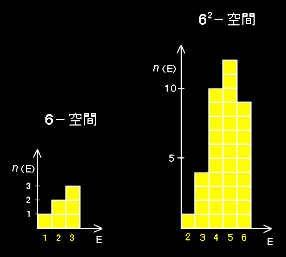 |
[ 1粒子 ]
[2粒子 ]
|
以上は古典統計です。
[5] 上で述べた2粒子状態について,量子統計性を導入して考えます。
6つのエネルギー準位のうちで占有されている粒子数を数表示でq=(n1,n2a,n2b,n3a,n3b,n3c) と書くことにします。例えば,n2b は,2bを占有する粒子数で,0か1(フェルミ粒子),または,0か1か2(ボース粒子)の値をとります。
r=[1,2a],または[2a,1]ならば,どちらも(110000)というように量子統計では書くことになります。これは同一粒子を区別しないことに相当します。下表には,古典統計の微視的状態と対応させて「粒子不区別」としてその状態を書き込みました。
古典的な状態数の数え方では,合計36個の状態があったものが,2つの粒子を区別しないことで,表の緑と赤とで示した合計の状態数,21個に減ります。
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[6] この21個が,ボース・アインシュタイン統計と呼ばれるものにあたります。さらに,この中から[xx]で表される占有状態 (⇒粒子不区別で2 が現れる占有状態 r )を除いた残りの状態だけを考えることが,フェルミ・ディラック統計に対応します。すなわち,21から6を差し引いた15個がフェルミ粒子に対する2粒子仮想3準位系で出現する状態の数ということです。
その違いを上図の茶色の背景で示した系のエネルギーが,E=4εの場合についてだけ図にしてみると下のようになります。
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
| E = 4ε のときの微視的状態数の数え方 古典統計では6+4=10通り,ボース統計では3+3=6通り,フェルミ統計では3+1=4通りの微視的状態が存在する。 なお,粒子Nに対してN!で古典統計の結果を除した修正古典統計は10÷2=5通りとなるが,具体的な微視的状態は図示不可能 (修正古典統計は所詮 ニセモノ なのだ)。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
[7] 統計性による状態数の違いをすべてのEについて表にまとめました。
| E | 2ε | 3ε | 4ε | 5ε | 6ε | 総状態数 |
| 占有状態 | (200) | (110) | (101) + (020) | (011) | (002) | |
| 古典統計 | 1 | 4 | 6 + 4 | 12 | 9 | 36 |
| ボース統計 | 1 | 2 | 3 + (2+1) | 6 | 3+3 | 21 |
| 修正古典統計 | 0.5 | 2 | 5 | 6 | 4.5 | 18 |
| フェルミ統計 |
0 | 2 | 3+1 | 6 | 3 | 15 |
一目瞭然ですが,状態数の数は統計性によって,
フェルミ統計 ≦ 修正古典統計 ≦ ボース統計 ≦ 古典統計
ところが,エネルギーがE=3ε,またはE=5εの場合だけを見てみると,
フェルミ統計 = 修正古典統計 = ボース統計 (各粒子のエネルギーが異なる)
が成り立っています。このときの2つの粒子の持つエネルギーは異なっており,一つの微視的状態には1つの粒子しか占有しえない状況となっています。
先程のE=4εの場合でも2粒子の占有する微視的状態のエネルギー準位が異なる(101)に制限して考えれば,3つの統計について,「 フェルミ統計=修正古典統計=ボース統計 =3」 が成り立ちます。一方,2つの粒子が同じエネルギー準位にあるE::(020)の場合は,3つの統計は一致しないことがわかります。
これは一般化することができ,
すべての粒子が異なる1粒子エネルギー状態を持つ場合,3つの統計は等しい結果を与える。
ということができます。このようなことが実現する状況は,高温状態 (エネルギー状態数が多い) であったり,そもそも粒子が極端に少ない=粒子密度が希薄なときに相当します。
フェルミ統計 = 修正古典統計 = ボース統計 (高温&希薄)
SUSTAINABLE TOKIWADAIGAK SINCE 2002