 |
104 調和振動子 1 |
| f-denshi.com 更新日:05/04/12 |
| サイト検索 |
1.調和振動子,ディラックの方法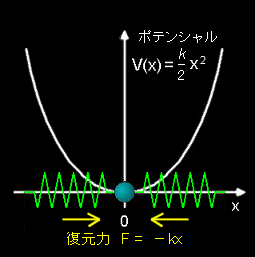
[1] 調和振動子とは,基準点(r=0)からの位置 r にあるときに復元力,
F =-kr
が働くような場で運動する質点のことをいいます。
1次元の場合を考えるとポテンシャル,
| V = |
k |
・x2 = |
mω2 |
・x2 ; ここで,ω=(k/m)1/2 |
|
|
| 2 |
2 |
の中の粒子の運動と考えることもできます。
このような場で運動している質点の全エネルギーは
| H = |
p2 |
+ |
mω2x2 |
= |
mω2 |
 |
x2+ |
p2 |
 |
・・・・・・・・・・・・ (1) |
|
|
|
|
| 2m |
2 |
2 |
m2ω2 |
|
[2]ここで,p ⇒ −ih |
∂ |
とすれば,シュレーディンガー方程式
|
|
| ∂x |
のハミルトニアンHになるのですが,ここでは計算をスマートに進めるために,ディラックの手法にならって位置演算子
x と運動量演算子 p とを組み合わせた次のような演算子を定義します。
| 消滅演算子: a = |
|
 |
x+ |
ip |
 |
・・・・・・・・・ (2) |
|
| mω |
| 生成演算子: a†= |
|
 |
x− |
ip |
 |
・・・・・・・・・ (3)
(消滅演算子の共役演算子) |
|
| mω |
逆に解けば,
[3] さらに, x0=(h/mω)1/2 とおいて,
| 消滅演算子: |
a ≡ |
1 |
 |
x+x02 |
i p |
 |
|
|
|
|
|
 |
2 |
x0 |
|
h |
|
| 位置演算子: |
x = |
x0 |
(a+a†) |
|
|
|
 |
2 |
|
|
|
|
| 運動量演算子:p = |
i h |
(a†−a) |
|
|
|
|
 |
2 |
x0 |
|
|
とした方が便利です。 消滅-生成演算子の交換関係は,[x,p]=ih なので[#],
[a,a†]=aa† − a†a = (1/2h){-i [x,p]+i [p,x]}=1
[4] さらに,個数演算子を次のように定義します。
しばらくこの演算子の性質について述べることにすると,まず,(2),(3)を代入して,
| N = a†a = |
mω |
 |
x2 + |
p2 |
 |
+ |
i |
[x,p] = |
H |
− |
1 |
|
|
|
|
|
2h |
m2ω2 |
2h |
h ω |
2 |
H について解いて,たいへん重要なハミルトニアンの個数演算子表示である
H ≡h ω(a†a+1/2) = h ω(N+1/2) |
という関係が得られます。よって,N と H と可換であって同時固有ケットが存在して同時対角化可能です[#]。すなわち,その固有ケットを|n>とすると,
H|n> = En|n> ・・・・・・・・・・・ [*]
N|n> = n|n> ・・・・・・・・・・・ [**]
のように書くことができるはずです。 ここで,En,n はそれぞれの演算子に対応する固有値です。また,
H|n> =h ω(N+1/2)|n>=h ω(n+1/2)|n>
と [*] とを比較して,
が得られます。
[5] さて,今度は n がいったいどんな値をとるのか調べたいのですが,N と a との交換関係,
[N ,a ]= - a ← [N ,a] = a†aa−aa†a = −[a,a†]a = −a なので
[N,a†]= a†
に注目します。これを用いれば,
Na|n> =( [ N,a ] + aN ) |n> = (n−1)a |n> ・・・・・・・・・・・・・・・・ (4)
Na†|n> =( [ N,a† ] +a†N )|n> = (n+1) a†|n> ・・・・・・・・・・・・・・・・ (5)
上式(4)をよく見ると,{ a | n> }は固有値が(n−1) である固有方程式[**] の固有関数であることを表していることに気が付きます。つまり,演算子 a は固有関数に作用して固有値が 1 だけ小さい固有関数を与えるのです。
a |n> → c|n-1> ( c: 比例定数 ) ←固有関数には定数倍の自由度があるので,
ここで,c は規格化条件から定まります。すなわち,各固有関数|n>が規格化されているとして,
<n|a†a|n> = <n-1|c†c|n-1> = |c|2
一方,次のような計算も可能です。
<n|a†a|n> = <n|N|n> = <n|n|n> = n
| したがって,c = |
|
|
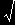 |
n |
|
であればよいことがわかります。 |
[6] 同様に,{ a†| n> }は固有値が (n+1) である固有方程式[**]の固有関数であることがわかります。
a を消滅演算子,a† を生成演算子と呼ぶのはこのような理由からです。
| a|n> = |
|
|
 |
n |
|
|n-1> |
| a†|n> = |
|
|
 |
n+1 |
|
|n+1> |
|
[7] 次に n が整数でなければならないことを示しましょう。今,ある固有関数|n> に a を次々と作用させていった場合を考えます。まず,n が整数であるならば,このときに得られる固有ケットの列
|
|
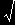 |
n |
|
|n-1>, |
|
|
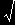 |
n(n−1) |
|
|n-2>,・・・, |
|
|
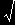 |
n(n−1) ・・・ 2・1 |
|
|0>,0 |
は最後に 0 となり,それ以上は a を作用させても意味がなくなります。
一方,n が整数でなければ,マイナスの整数でないnで表される | n> の項を持つ固有ケットの列が無限に続くことになります。しかし,量子力学の基本要請から確率の意味を有するケットのノルムは正でなければならない,すなわち,
(<n|a†)(a|n>)≧0
を要請すると, <n|a† a|n>=<n|N|n>=n なので結局,
n≧0
でなければならないことがわかります。すなわち,n は整数でなければならず,しかも,0
が最小値となります。このとき,エネルギーが最低の基底状態 |0> での固有エネルギーは
E0 =(1/2)h ω です。
[8] 逆に,|0> に生成演算子を次々と作用させていけば,n=1,2,3,・・・の励起状態にある固有ケットを |0>で表すことができます。
|1>=a†|0>
| |2>= |
a† |
|1>= |
(a†)2 |
|0> |
|
|
|
|
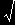 |
2 |
|
|
|
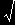 |
2 |
|
・・・・・・・・・・
| |n>= |
(a†)n |
|0> |
|
|
|
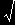 |
n! |
|
まとめ
調和振動子と個数演算子の固有値と固有ケット
H|n>=En|n> : En=(n+1/2)h ω ; ω=(k/m)1/2
N|n>= n|n> : n=0,1,2,3,・・・
| |n>= |
(a†)n |
|0> |
|
|
|
 |
n! |
|
|
2. 固有ケットの x−表示
[1] 固有ケット |n> に位置 x' のブラ <x'| をかけて得られる表示 <x'|n> を |n>の x -表示と言います[#],[#]。要するに位置座標 x'の関数としての具体的な形のことですが,ここではこれを求めてみましょう。
a|0>=0 に左から <x'|をかけて,a の定式義[#]を用いれば,
| 0=<x'|a|0>= |
1 |
<x'| |
x+ |
i p |
|0> |
|
|
|
|
|
 |
2 |
x0 |
|
mω |
| ↓ |
ここで, <x'|x|0> = x'<x'|0> |
および, <x'|p|0> = −ih |
∂ |
<x'|0> を用いると, |
|
| ∂x' |
| = |
 |
x'+x02 |
d |
 |
<x'|0> |
|
| dx' |
| ⇔ |
d |
<x'|0>=− |
x' |
<x'|0> |
|
|
| dx' |
x02 |
この微分方程式の規格化された解は,
| <x'|0>= |
1 |
exp |
 |
− |
1 |
 |
x' |
 |
2 |
 |
← 基底状態の波動関数:ψ0(x)です。 |
|
|
|
|
|
|
|
| π1/4 |
 |
x0 |
|
2 |
x0 |
|
となります。さらに生成演算子 a† [#] を利用して,|1>,|2>,・・・の具体的な関数形を求めることができます。
| <x'|1>=<x'|a†|0>= |
1 |
<x'| |
x− |
i p |
|0>= |
1 |
 |
x'−x02 |
d |
 |
<x'|0> |
|
|
|
|
|
|
|
 |
2 |
x0 |
|
mω |
|
|
|
 |
2 |
x0 |
|
dx' |
| <x'|2>= |
1 |
<x'|(a†)2|0>= |
|
1 |
・ |
 |
1 |
 |
|
x'−x02 |
d |
 |
 |
2 |
<x'|0> |
|
|
|
|
|
|
|
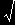 |
2 |
|
|
|
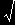 |
2! |
|
|
|
|
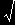 |
2 |
x0 |
|
dx' |
|
これを続けると,次の結果を得ることができます。
| <x'|n>= |
1 |
・ |
1 |
 |
x'−x02 |
d |
 |
n |
exp |
 |
− |
1 |
 |
x' |
 |
2 |
 |
|
|
|
|
|
|
|
|
|
|
| π1/4 |
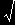 |
x0 |
|
|
|
|
 |
2n・n! |
(x0)n |
|
dx' |
2 |
x0 |
|
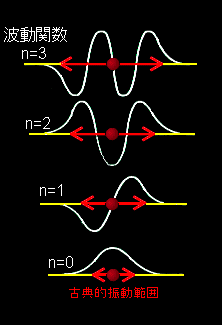
[ 調和振動子の波動関数 <x'|n> ]
| <x'|n>= |
|
1 |
 |
x'−x02 |
d |
 |
n |
<x'|0> |
|
|
|
|
|
|
 |
2n・n! |
(x0)n |
|
dx' |
|
|
ただし,
| <x'|0>= |
1 |
exp |
 |
− |
1 |
 |
x' |
 |
2 |
 |
|
|
|
|
|
|
|
| π1/4 |
 |
x0 |
|
2 |
x0 |
|
x0=(h/mω)1/2 |
 |
|
[目次]
