Appendix 2  行列力学入門 ２　ブラケット記法）
f-denshi.com  更新日：
サイト検索

１．状態ケットと演算子の成分表示

［１］ある物理状態を表す状態ケット|ψ＞ が線形演算子 A の固有ケットからなる基底Σ：｛|a₁＞，|a₂＞，･･･，|a_n＞｝ の線形結合で，

|ψ＞＝c₁|a₁＞＋c₂|a₂＞＋･･･＋c_n|a_n＞　　　　　　　･････　[*]

と表せる場合を考えます。 規格化されている固有ケットは，＜a_ｊ|a_k＞＝δ_jk　なる関係があるので，[*]式の両辺に左から ＜a_k| をかけてやれば，

＜a_k|ψ＞＝c_k                      

となります。したがって，|ψ＞ はベクトル成分を用いれば，

|ψ＞＝ c1  ＝ ＜a1|ψ＞ c2 ＜a2|ψ＞ ： ： cn ＜an|ψ＞

 と表せます[#]。これを，「状態ケット |ψ＞の基底Σ による表示（＝ベクトル表現）」 といいます。

［２］ 二つのベクトルx，y  のテンソル積[#]から作られる行列 （２階テンソル）

|x＞＜y|＝

x1 （y*1，y*2，･･･，y*n） ＝ x1y*1･･･････x1y*n x2 ･･････････････ 　： ･･････････････ xn xny*1･･･････xny*n

は線形演算子です。　特にベクトルとして固有ケットを用いた場合，

|aj＞＜ak|＝ 0･･ 0 ･････0 0･･ 0 ･････0 0･･ 1 ･････0 ←j 行目 ･･･ ･･ ･･････ 0･･ 0 ･････0 ↑ 　　k 列目

という j 行 k 列 成分だけが 1 で他は 0 という行列となります。したがって，数 c について，|a_j＞c_jk＜a_k| を考えると，これは j 行 k 列成分がc_jk で，他の成分が 0 である行列を意味します。すると，n²個の任意の数c_jkについて次のような和を考えると，

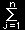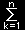|aj＞cjk＜ak|＝		c11	c12･･･	c1n		･･･  [**]
		c21	c22･･･	c2n
		：	･････	：
		cn1	cn2･･･	cnn

となり，これは任意の c_jk を成分とするｎ次正方行列です。

［３］　これをふまえ，いくつか重要な演算子を定義します。まず，

（１）　射影演算子　Λk＝|ak＞＜ak|　　　　[ck|ak＞ を選び出す]

例えば，　＜a_k|a_j＞＝δ_jk なので，
　　　Λ_k|ψ＞＝|a_k＞＜a_k|｛c₁|a₁＞＋c₂|a₂＞＋･･･＋c_n|a_n＞｝
　　　　　　　　　＝|a_k＞｛c_k＜a_k|a_k＞｝
　　　　　　　　　＝c_k|a_k＞

と計算され，c_k|a_k＞ を選び出す働きがあります。したがって，すべてのk について足し合わせた，

（２）　恒等演算子 　I 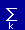＝ |ak＞＜ak|　          [何も変化させない]

を考えると，これは，ケットに何も影響を及ぼさない演算子となります。実際，

I |ψ＞＝

|ak＞＜ak|｛

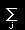cj|aj＞｝

＝

|ak＞＜ak|ck|ak＞

＝

|ak＞ck

　　　　　　　＝|ψ＞

もちろん，恒等演算子は単位行列と同じです。この恒等演算子 I の利用方法として，つじつまの合う行列計算ができるような任意の位置に挿入します。例えば，任意の演算子をA，B　として，

AB|ψ＞＝AIB|ψ＞  　＝

A|ak＞＜ak|B |ψ＞

AB|ψ＞＝AIBI|ψ＞＝

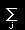A|ak＞＜ak|B| aj＞＜aj|ψ＞

などとすることが可能です。　　　

［４］　任意の線形演算子T は２つの恒等演算子を挟むと，

Ｔ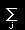＝ |aj＞＜aj|Ｔ|ak＞＜ak|

ここで，[**]を思い出すと，j 行 k 列成分が ＜a_j|Ｔ|a_k＞ である行列 [#]，

T ＝		＜a1|T|a1＞　＜a1|T|a2＞　････＜a1|T|an＞
		＜a2|T|a1＞　＜a2|T|a2＞　････＜a2|T|an＞
		･･･････････････････････････････
		＜an|T|a1＞　＜an|T|a2＞　････＜an|T|an＞

が T であることがわかります。これを，「演算子T の基底Σ による表示（＝行列表現）」といいます。

［５］　特に，T＝A　（A|a_k＞＝a_k|a_k＞） のときは，

A ＝

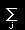|aj＞＜aj|A|ak＞＜ak|

＝

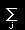|aj＞＜aj|ak|ak＞＜ak|

＝

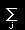ak|aj＞＜aj|ak＞＜ak|

＝

ak|ak＞＜ak|

＝

akΛk

＝ ΣakΛk

となります。つまり，演算子A はその固有値と射影演算子との積で表すことができます。

２．基底変換とその成分表示

［１］　２つの正規直交系の間を結ぶ基底変換，

｛|a1＞，|a2＞，･･･，|an＞｝	⇒	｛|b1＞，|b2＞，･･･，|bn＞｝
基底Σ	U	基底Σ'

を表すユニタリ行列 U はどのように「表現」できるのでしょうか。 ２つの基底の関係が

|b1＞ ＝ U|a1＞ |b2＞ ＝ U|a2＞ 　　　････････ |bn＞ ＝ U|an＞

⇒　 ブラだと

＜b1| ＝ ＜a1|U* ＜b2| ＝ ＜a2|U* 　　　　　････････ ＜bn| ＝ ＜an|U*

つまり，

基底｛|a1＞，･･･，|an＞｝ と 基底｛|b1＞，･･･，|bn＞｝ との関係   |bk＞＝U|ak＞   もしくは，   ＜bk|＝＜ak|U*　    k ＝ 1，2，･･･，n

で与えられるとき，これを満たすU は，＜a_j|a_k＞＝δ_jk ，＜b_j|b_k＞＝δ_jk に注意すれば，

（３）  基底変換演算子： 　U ＝|b1＞＜a1|＋|b2＞＜a2|＋･････＋|bn＞＜an|　　 　   ＝ |bj＞＜aj| 　 もしくは，  U*＝ |aj＞＜bj|

と置けばよいことがわかります。実際に計算して，

U|ak＞＝｛

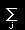|bj＞＜aj|｝|ak＞

             ＝ |b_k＞

と確かめられます。

［２］　さらに，

UU* ＝ ｛

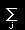|bj＞＜aj|｝｛

|ak＞＜bk|｝

＝

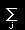|bj＞＜aj|ak＞＜bk|

＝

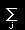|bj＞＜bj|

　　　 ＝    I

が確かめられます。 U^*U ＝ I　も同様に示すことができ，この正規直交系から正規直交系への基底変換演算子U がユニタリ行列（U^*＝U^-1）である[#]ことをブラ･ケットで示したことになります。　U の「基底Σ での行列表示」は，

U  ＝

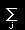|aj＞＜aj|U|ak＞＜ak|

基底変換演算子U の j 行 k 列目の行列成分：　 　         ＜aj|U|ak＞＝＜aj|bk＞

で得られます。状態ケットの成分（ベクトル成分）は，

任意の状態ケットの基底変換    ＜bj|ψ＞＝ ＜bj|ak＞＜ak|ψ＞                    ↓　     ＜bk| ＝ ＜ak|U*を用いて，               ＝ ＜aj|U*|ak＞＜ak|ψ＞　　←　（数学では　x’＝U*x　⇔　x＝Ux’ と書く）

で与えられますこれを具体的に行列，ベクトルで書くと，

	＜b1|ψ＞		＝		＜a1|U*|a1＞　＜a1|U*|a2＞　･･･＜a1|U*|an＞			＜a1|ψ＞
	＜b2|ψ＞				＜a2|U*|a1＞　＜a2|U*|a2＞　･･･＜a2|U*|an＞			＜a2|ψ＞
	：				･････････････････････････････････････････			：
	＜bn|ψ＞				＜an|U*|a1＞　＜an|U*|a2＞　･･･＜an|U*|an＞			＜an|ψ＞
基底Σ'で表示したψ					基底変換行列	基底Σで表示したψ

となります。同様に，

任意の演算子の基底変換    ＜bj|Ｔ|bk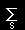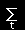＞＝ ＜bj|as＞＜as|Ｔ|at＞＜at|bk＞                  ↓　     ＜bk| ＝ ＜ak|U*，　|bk＞＝ U|ak＞を用いて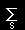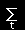，                   ＝ ＜aj|U*|as＞＜as|Ｔ|at＞＜at|U|ak＞ ＜bj|Ｔ|bk＞＝ ΣΣ＜bj|as＞＜as|Ｔ|at＞＜at|bk＞ 　　　　　　　　　   ＝ ΣΣ＜aj|U*|as＞＜as|Ｔ|at＞＜at|U|ak＞ 　　　　　　　　　　　　　　　　　　　　　　　　　　　　      　　↑　（数学では，　T’＝U*TU　と書く）

左辺は基底Σ'で表示した演算子Tの行列成分，右辺は基底Σで表示した演算子Tのい行列成分と基底変換演算子の行列成分を表しています。

［目次へ］

もうひとつ，追加