８　可動端変分問題
f-denshi.com  最終更新日：　03/03/18
サイト検索

１．片側自由端変分問題

［１]　　光学において，フェルマーの原理：

「光は所要時間が最小となるように経路を選んで進む。」

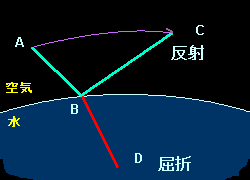
というものがありますが，光が均一な媒質中をA→C(右図)と進む場合は前節の議論，すなわち固定端変分問題の取り扱いがそのまま使えます。しかし，光の反射［A→B→C]や屈折[A→B→D] のような現象がおきている問題には適用できません。媒質の性質が不連続に変わるB点で ”求めるべき曲線” は微分不可能だからです。つまり，解曲線C²の関数とする議論が使うことができないのです。

［２]　この章ではこのような問題について考えます。右図の［A→B→C]の経路において，A，Cは問題の設定から与えられる固定端ですが，B点は答えが得られるまではどこにあるのかわかりません。したがって，問題となる汎関数の積分はA→BとB→Cの２つの区間の和として表されるはずですが，それぞれ積分範囲の片側が定まらない状況下で問題を解くことになります。このような問題を(片側)可動端変分問題と言います。ただし，この問題では，反射点，または屈折点Bは空気と水との界面：y＝g(t)上にあることは明らかなのでこれを境界条件として付加する必要があります。

［３]　点Bがどこにあるかわからないといいましたが，この問題に答えが唯一存在するならば，B点は定まっているバズです。この定点B点とA点とを両端にもつ積分の問題は第１章の固定端変分問題と同じになり，同じ解(オイラー方程式)を与えることになるはずです。

　問題エッセンスを抽出すると次のようになります。

S[ｙ(t)]＝ F［t,y(t),y'(t)]dt の極値条件を求めよ。ただし， 　　y'(t)＝ dy ，F［t,y(t),y'(t)]∈C3［a,b]　( a≦t≦bで３階連続微分可能な関数全体の集合 ) ｄt および， 　　y(tB)＝g(tB)  ：  gは与えられた関数

２．横断性の条件　[ B点を求める式 ]

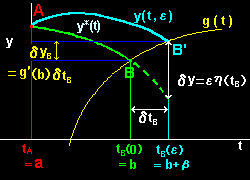
［１]　正のβに対して，t の区間 [a,b＋β] での比較曲線：y(t,ε)を

　　y(t,ε)＝ｙ^*(t)＋εη(t)＝ｙ^*(t)＋δy
　　　　　ｙ^*(t)：正解の曲線　［右図の曲線A→B]
　　　　　η(a) ＝0
　　　　　η(b)≠0
　　　　　δy＝δy(t,ε)＝εη(t)

とします。この関数を用いて次の汎関数も定義します。

φ(ε)＝S[ｙ(t,ε)]＝ F［t,y(t,ε),y'(t,ε)]dt

［２]　固定端変分問題のときと違って，εの変化に応じて，B点はB'点に移動し，積分範囲もそれに応じて，
［a,b]から［a,b＋β]，　このB'端の座標をεを用いて，

t−座標：　b＝t_B(0)　，b＋β＝t_B(ε)
y−座標：　y(t_B(ε),ε)＝ｙ^*(t_B(ε))＋εη(t_B(ε))　　

と表すことにします。　また，ε＝0　のとき，

y(t_B(0),0)＝ｙ^*(t_B(0))＝ｙ^*(b)

また，B'がy＝g(t)上にあるという境界条件[#]から

　　　　y(t_B(ε),ε)＝g(t_B(ε))　⇔　ｙ^*(t_B(ε))＋εη(t_B(ε))＝g(t_B(ε))

これをεで微分してから，ε＝0 として，

ｙ^*'(b)t_B'(0)＋η(b)＝g'(b)･t_B'(0)　　　　　←　t_B(0)＝b　

［３]　すなわち，         ↑ ｙ^*'は t による微分，t_B'はεによる微分です＝合成関数の微分

η(b)＝(g'(b)−ｙ*'(b))tB'(0)

が成り立ちます。これを用いると，(　t_B(0)＝b　に注意)

φ'(ε)＝		d		Fdt ＝	d		Fdt＋	d		Fdt
		dε			dε			dε

なので(積分範囲の分割)，　第一項は［A，B]における固定端変分問題[#]と同じことに注意すれば，

φ'(ε)＝			(Fy	∂ｙ	＋Ｆy'	∂y'	)dt＋	d		Fdt
				∂ε		∂ε		dε

したがって，   (　↓　最後の項は　　d/dε＝(d/dt)(dt/dε)を使って　)

φ'(0)＝

［Fyη＋Ｆy'η']ε=0 dt＋［F]t=b･tB'(0) ＝ 0

↓　一つ目の積分の第２項を部分積分して

φ'(0)＝			(Fyη−	d	Ｆy')η(t)dt＋［Fy'･η]		＋［F]t=b･tB'(0)＝0
				dt

最初の積分はE-L方程式が成り立つときは0，また，η(a)＝0　なので，

φ'(0)＝　0　　＋［F_y'η]_t＝b　　＋［F]_t=b･t_B'(0)

＝［F_y']_t＝bη(b)＋［F]_t=b･t_B'(0)　　　　　　　↓　η(b)を消去[#]　　　

＝［F_y']_t＝b(g'(b)−ｙ^*'(b))t_B'(0)＋［F]_t=b･t_B'(0)

＝｛［F_y']_t＝b(g'(b)−ｙ^*'(b))＋［F]_t=b｝ t_B'(0)　＝0

ここで導関数　t_B'(0)はg(t)や，点Bの一などによっていろいろ変わるので，常にφ'(0)＝0　が成立するために　ｙ^*の満たすべき条件は，｛　｝内が0でなければなりません。これを端点Bにおける横断の条件いいます。つまり，解曲線，ｙ^*(t)はEL方程式に加えてさらに下の条件が付加されます。

３．完全自由端問題

［１]　まず，片側自由端の第一変分は求めると，

     δS＝φ'(0)･ε

＝			(Fy−	d	Ｆy')η(t)εdt＋｛［g'(b)−ｙ*'(b)]･[Fy']t＝b＋[F]t＝b}･tB'(0)ε
				dt

↓	δy≡η(t)ε 　　　δtB≡tB'(0)εとおいて

＝			(Fy−	d	Ｆy')δy dt＋｛［g'(b)−ｙ'(b)]･[Fy']t＝b＋[F]t＝b}･δtB
				dt

↓　　　　g'(b)＝	δyB	を用いて，(Bがy＝g(t)上にあるので)
	δtB

＝			(Fy−	d	Ｆy')δydt＋｛[Fy']t＝b}･δyB＋｛[F]t＝b−ｙ'(b)･[Fy']t＝b}･δtB
				dt

となります。　ここまではBが曲線g(t)上にあるとして計算しましたが，もし，Bが曲線g(t)上にある必要がないとき(←完全自由端という)はδy_Bとδt_Bが独立に動くことができるので，δy_B，δt_B　の係数｛　｝が0でなければならないのです。

［ 目次へ ]