| 4 ホモロジー群(1) | ||
| f-denshi.com [目次へ] 最終更新日:23/11/30 校正中 | ||
| サイト検索 | ||
[1] ホモロジー群 Hq(X) とは,図形 X に対して,
H0(X) = Zk0 k0:連結な成分の数
H1(X) = Zk1 k1:ループの数 (=面の境界でない閉曲線)
H2(X) = Zk2 k2:閉曲面に囲まれる空洞の数 (=立体の境界でない閉曲面)
:
Hq(X) = Rkq kq:q次元の「空洞」の数
という意味を持ちます。この性質が位相不変性を持つために,ある2つの図形 (=|複体 K|)が位相同型でないことを示すときにしばしば有用となります。
具体的な計算例として,(1)四面体(3次元),(2)四面体面(2次元),(3)四面体輪(1次元),
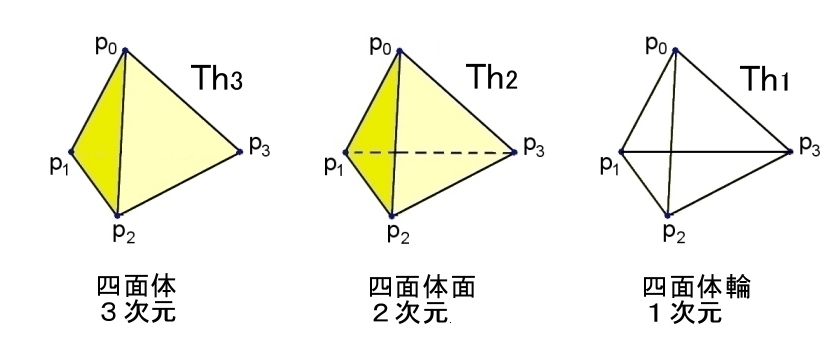
のホモロジー群を示しておくと,以下のとおりとなります。
| |K|= | 四面体 Th3 |
四面体面 Th2 |
四面体輪 Th1 |
| H3(K) | { 0 } | { 0 } | { 0 } |
| H2(K) | { 0 } | Z | { 0 } |
| H1(K) | { 0 } | { 0 } | Z3 |
| H0(K) | Z | Z | Z |
すべての図形は1つの連結成分から構成されており,四面体面にはこの閉曲面に囲まれている空洞が1つあり,向き付け可能であること,また,四面体輪にはループが3つ存在するということなどが分かります。
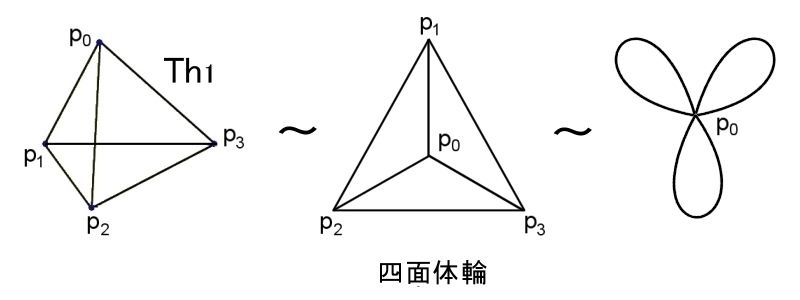
(一般的に H1(K) は基本群π1(K,p0) を可換化したものに等しい。)
[2] それでは,ホモロジー群の定義,計算に必要な用語を順に説明していきましょう。
まず,q次元鎖群の定義です。
|
定義 q次元鎖群 n次元複体K に属する r個の q (次元)単体をσ1q,σ2q,…,σrq とする。これら各σjq について ”向き” を与えた有向q単体を <σjq> と表し,それと逆向きの単体は−<σjq> と表す。 これらの有向q単体に整数係数を付けた線形結合,
を 複体K のq次元鎖と呼び,q次元鎖全体からなる集合を Cq(K) と表す。 Cq(K) は加法群となるように演算(<σ1q>,・・・,<σrq> を基底とするベクトル空間の加法として)を定めることができるが,これをq次元鎖群と呼び,これも Cq(K) と表す。 |
具体的に見ていった方が分かりやすいでしょう。
[3] 複体として,四面体 (Th3),-面 (Th2),-輪 (Th1) の有向単体の集合を書いておきます。
K^(Th3)={ <p0p1p2p3>,
<p1p2p3>,<p0p2p3>,<p0p1p3>,<p0p1p2>,
<p0p1>,<p0p2>,<p0p3>,<p1p2>,<p1p3>,<p2p3>,
<p0>,<p1>,<p2>,<p3> }
K^(Th2)={ <p1p2p3>,<p0p2p3>,<p0p1p3>,<p0p1p2>,
<p0p1>,<p0p2>,<p0p3>,<p1p2>,<p1p3>,<p2p3>,
<p0>,<p1>,<p2>,<p3> }
K^(Th1)={ <p0p1>,<p0p2>,<p0p3>,<p1p2>,<p1p3>,<p2p3>,
<p0>,<p1>,<p2>,<p3> }
↑ 有向複体とでも呼ぶような集合です。

[4] これらのq次元鎖について,次元ごとに説明していきます。
(1) q=0
σ0の向きは<ps>の向きを便宜的に正方向とする有向0単体とし,これにマイナスの符号を付けた−<ps>は反対の向きをもつと考えます。 <σj0> → <ps> と書き直す。
このとき,複体Kのすべての 0単体 <pi >に向きを与えておいて,任意の整数係数 mi を掛けて足し合わせたものの全体集合,
C0(K) = {ms <ps>| ms∈ Z,<ps >∈有向0単体) } [0次元鎖群]
は加群となります。
四面体であれば,
C0(Th3)={ m0<p0>+m1<p1>+m2<p2>+m3<p3>|m0,m1,m2,m3 ∈ Z }
これは <p0>,<p1>,<p2>,<p3> を基底とする整数係数をもつ3次元ベクトル空間 〜 Z4 とみなせます。
(2) q=1
Kの1単体σj2に対して,| pspt| に対して,psからptへの向きが与えられるときは,<pspt>と書いて有向1単体とします。 <σj1> → <pst>
有向1単体σ1の向きは<pspt>を正方向とすれば,下添字を互換した <ptps>=−<pspt> を負方向となります。
このとき,複体Kのすべての1単体<pspt >に向きを与えておいて,任意の整数係数 mst を掛けて足し合わせたものの全体集合,
C1(K) = {mst <pspt >| mst ∈ Z,<pspt >∈有向1単体 } [1次元鎖群]
は加群となります。四面体であれば,
C1(Th3)={ n1<p1p2>+n2<p2p3>+n3<p3p1>+n4<p0p1>+n5<p0p2>+n6<p0p3>
|n1n2,n3,n4,n5,n6 ∈ Z }
これは <p0p1>,<p1p2>,<p2p0> を基底とする整数係数をもつ3次元ベクトル空間 〜 Z6 とみなせます。
(3) q=2 有向2単体
2次元単体σ2(三角形)の向きは<psptpu>の下添え字を置換したとき,
σ2の向き= <psptpu>のその偶置換を正方向 <psptpu>のその奇置換を負方向
とします。<σj2> → <pstu> (↑逆方向に定義してもよい。)
有向2単体σ2の向きは<psptpu>を正方向とすれば,下添字を互換した <ptpspu>=−<psptpu> は負方向となります。
その全体集合は,
C2(K) = {mstu<psptpu>| mstu ∈ Z,<psptpu >∈有向2単体 } [2次元鎖群]
は加群となります。
四面体面であれば,
C2(Th3) ={ m0<p1p2p3>+m1<p0p3p2>+m2<p0p1p3>+m3<p0p2p1>| m0,m1,m2,m3 ∈ Z }
これは <p1p2p3>,<p0p3p2>,<p0p1p3>,<p0p2p1> を基底とする整数係数をもつ4次元ベクトル空間 〜 Z4 とみなせます。
(4) 有向 q (≧3) 単体
q ≧3の複体に対して,σqの向きは,<pspt・・・pq> を基準に,
σqの向き= <pspt・・・pq> のその偶置換を正方向 <pspt・・・pq> のその奇置換を負方向
としておきます。
Cq(K) = {mst…q<pspt・・・pq>| mst…q ∈ Z,<pspt・・・pq>∈有向q単体 } [q次元鎖群]
四面体の3次元単体であれば,
C3(Th3) = { m<p0p1p2p3>| m ∈ Z }
これは <p0p1p2p3> を基底とする整数係数をもつ1次元ベクトル空間 〜 Z とみなせます。
[5] 以上まとめると,
四面体の鎖群
Ck(Th3)={ ck=0|k≧4 }
C3(Th3)={ c3=m<p0p1p2p3>|m∈Z }
C2(Th3)={ c2=m0<p1p2p3>+m1<p0p3p2>+m2<p0p1p3>+m3<p0p2p1>|mk∈Z}
C1(Th3)={ c1=n1<p1p2>+n2<p2p3>+n3<p3p1>+n4<p0p1>+n5<p0p2>+n6<p0p3>|nj∈Z }
C0(Th3)={ c0=d0<p0>+d1<p1>+d2<p2>+d3<p3>|dk∈Z }
( ここで,k=1,2,3,4, j=1,2,3,4,5,6 )
四面体面 Th2では,Ck (k≧4) に加えてC3={ 0 },
四面体輪 Th1では,Ck (k≧4) に加えてC3=C2={ 0 } となる。次元だけ書いておくと,
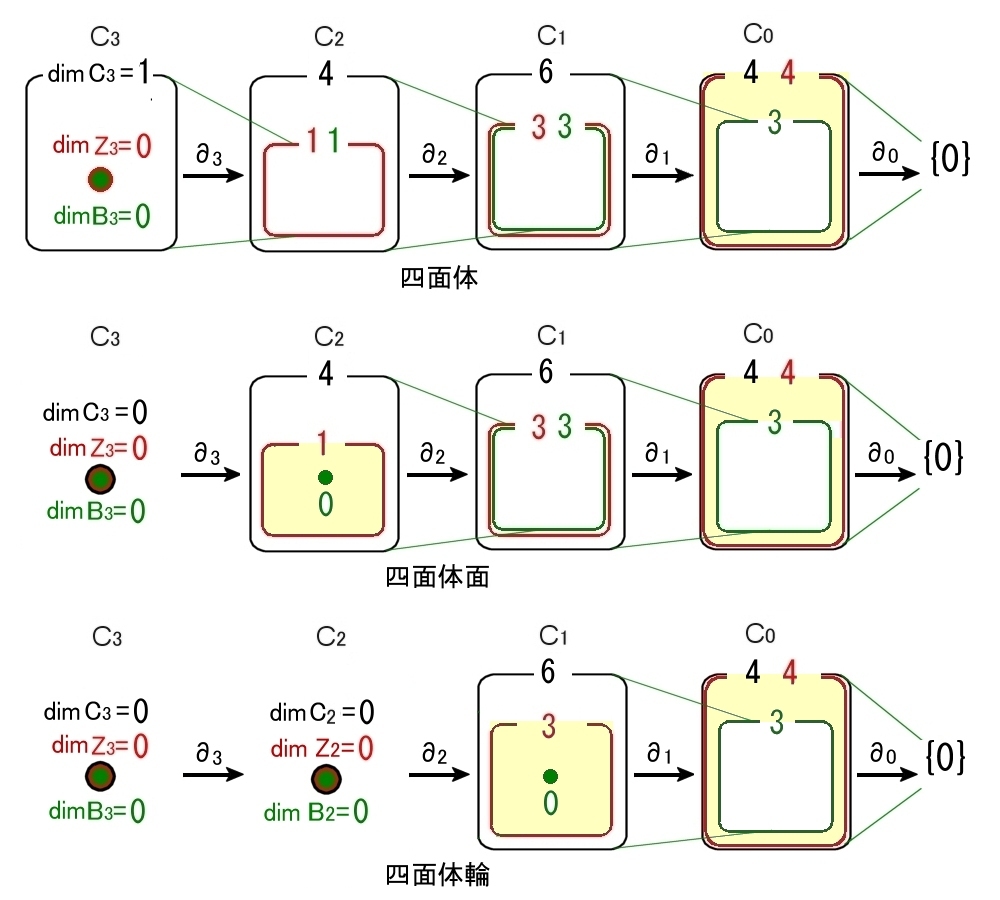
K dim C4(K) dim C3(K) dim C2(K) dim C1(K) dim C0(K) 四面体 0 1 4 6 4 四面体面 0 0 4 6 4 四面体輪 0 0 0 6 4
[6] 次に q 次元鎖から q-1 次元鎖への境界準同型(写像)と呼ばれる写像を次のように定義ます。
|
定義 複体K の q次元有向単体,<σq>=<p0p1…pq> に対して,境界準同型(写像) ∂q<σq> を以下のように定義する。
( pkはこれを除くという意味) ∂q<σq> は q−1次元鎖となり,∂q<σq>∈Cq-1(K) である。 さらに,q次元鎖,
に対して境界準同型(写像)∂q: Cq → Cq-1 を以下のように定義する。
|
例1
境界の存在する2次元の三角形 σ2 の境界準同型は,
∂2(<p0p1p2>=(<p1p2>−<p0p2>+<p0p1>)
( ≠0 )
となります。
[7]
例2 境界の存在しない1次元の三角形の輪の1次元鎖の一つ,
c1=<p0p1>+<p1p2>+<p2p0>
の境界準同型は,
∂1(c1)=∂1(<p0p1>+<p1p2>+<p2p0>)
=<p1>−<p0>+<p2>−<p1>+<p0>−<p2>)
=0
例3 境界の存在しない四面体面を考えます。
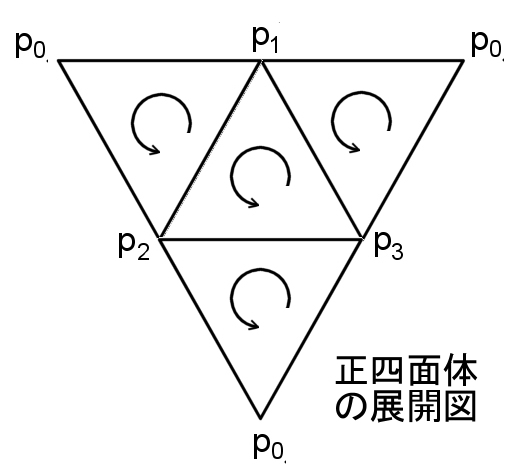
ここで,向きが上のように定められた2次元鎖の一つを,
c2=<p1p2p3>+<p0p3p2>+<p0p1p3>+<p0p2p1> ( =∂3<p0p1p2p3> )
とすると,
∂2(c2)=∂<p1p2p3>+∂<p0p3p2>+∂<p0p1p3>+∂<p0p2p1>
= <p2p3>−<p1p3>+<p1p2>
+<p3p2>−<p0p2>+<p0p3>
+<p1p3>−<p0p3>+<p0p1>
+<p2p1>−<p0p1>+<p0p2>
=<p2p3>+<p1p2>+<p3p2>+<p2p1>
=0
が成り立っています。
一般的に,
∂q(cq)=0
であるとき,cq をq次元サイクルといいます。言い換えると,境界が存在しない q次元鎖 cq を q次元サイクルといいます。
[8] 一般化して,
|
定義 q次元サイクルの全体集合 を Zq(K)=Ker∂q と表して輪体群(またはサイクル群)と呼ぶ。 |
と定義しておきましょう。先に示した四面体面ならば,
∂2(c2) ∈ Z2(Th2)
ということです。
[9]
|
命題 ∂q(∂q+1) = 0 |
任意の cq+1∈Cq+1(K) について,2回続けて境界準同型をとると 0 になる,すなわち,
Im∂q+1(cq+1) ⊂ Ker∂q ⊂ Cq(K) ⇔ Bq(K)⊂Zq(K)⊂Cq(K)
が成り立つということです。
証明は,有向単体の境界準同型の定義式 [*] 式から,∂q(∂q+1) によって現れるk番目とj番目(j≠k) 2つの点を除いた <p0p1…pk…pj…pq> という2つの項に掛かる符号が k と j のどちらを先に除いて得られたかによって反対となることから分かります。
[10] この命題より,任意の q+1次元鎖 cq+1 の境界準同型∂q+1(cq+1) はq次元サイクルとなっている,すなわち,∂q+1(cq+1) ∈Ker(∂q) です。 そのような q次元サイクルに次のとおり名前を付けておきます。
|
定義 複体K の任意の q+1次元鎖 cq+1 の境界準同型∂q+1(cq+1) を Bq(K)=Im∂q+1 と表して境界輪体群(またはバウンダリ群)と呼ぶ。 |
[11] 以上の定義を用いてホモロジー群の定義を次のように与えることができます。
|
定義 輪体群を境界輪体群で割った剰余群, Hq(K)=Zq(K)/Bq(K)をホモロジー群という。 |
つまり,加群として,
Bq(K) ⊂ Zq(K) ⊂Cq(K)
が成り立ちますが,Zq(K) において Bq(K)=0 とみなす剰余群をホモロジー群の定義とするということです。
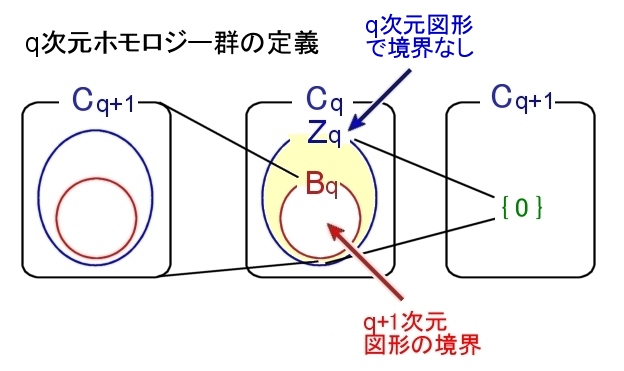
これ定義の意味するところは,
Kのホモロジー群 Hq(K) が { 0 } でなければ,|K|は,
「境界のない q次元図形で, q+1次元図形の境界になっていない。」
ことが分かります。
[13]
例4 定義に従って下記の図形の輪体群,境界輪体群,ホモロジー群を求めよう。

(1) 四面体,四面体面,四面体輪の場合
C4(Th3)=C4(Th2)=C4(Th1)={ 0 } で,準同型写像において単位元は単位元に写るので,
B3(Th3)=B3(Th2)=B3(Th1)=Im∂4 { 0 }={ 0 } ←整数加群の単位元
(2−1) 四面体の場合
C3(Th3)={ c3=m<p0p1p2p3>|m∈Z } なので,
B2(Th3)=Im∂3c3
∂3c3=m(<p1p2p3>−<p0p2p3>+<p0p1p3>−<p0p1p2>) ・・・[*]
よって,B2(Th3) 〜 Z
また,Ker∂3=0 となるのは,[*] 式で m=0 のときなので,
Z3(Th3)={ 0 }
(2−2) 四面体面,四面体輪の場合
C3(Th2)=C3(Th1)={ 0 } なので,
B2(Th2)=B2(Th1)=Im∂3{ 0 }={ 0 }
(3−1) 四面体,四面体面の場合
C2(Th3)=C2(Th2)
={ c2=m0<p1p2p3>+m1<p0p3p2>+m2<p0p1p3>+m3<p0p2p1>|mk∈Z,k=0,1,2,3 }
B1(Th3)=B1(Th2)=Im∂2c2
∂2c2=∂(m0<p1p2p3>+m1<p0p3p2>+m2<p0p1p3>+m3<p0p2p1>)
= m0(<p2p3>−<p1p3>+<p1p2>)
+m1(<p3p2>−<p0p2>+<p0p3>)
+m2(<p1p3>−<p0p3>+<p0p1>
+m3(<p2p1>−<p0p1>+<p0p2>)
=(m0-m1)<p2p3>+(m0-m2)<p3p1>+(m0-m3)<p1p2>
+((m2-m0+m0-m3))<p0p1>+((m3-m0+m0−m1))<p0p2>+((m1-m0+m0−m2))<p0p3>
=m'1<p2p3>+m'2<p3p1>+m'3<p1p2>
+(m'3−m'2)<p0p1>+(m'1−m'3)<p0p2>+(m'2−m'1)<p0p3>
=m'1(<p2p3>+<p0p2>−<p0p3>)
+m'2(<p3p1>+<p0p3>−<p0p1>)
+m'3(<p1p2>+<p0p1>−<p0p2>)
すなわち,B1(Th3)=B1(Th2) 〜 Z3
(ただし, m'1,m'2,m'3∈Z, m'k≡m0−mk; k=1,2,3 )
次に ∂2c2=0 より Z2(Th3)=Z2(Th2) を求めるが,上の結果より,
∂2c2=m'1(<p2p3>+<p0p2>−<p0p3>)
+m'2(<p3p1>+<p0p3>−<p0p1>)
+m'3(<p1p2>+<p0p1>−<p0p2>)
これが,0 となるのは,m'1=m'2=m'3=0 のとき,すなわち,
m1=m2=m3=m0
よって,
c2=m0 ( <p1p2p3>+<p0p3p2>+<p0p1p3>+<p0p2p1> ) ∈ Ker∂2
(m0 ∈ Z )
であればよい。
すなわち, Z2(Th3)=Z2(Th2) 〜 Z
(3−2)
四面体輪の場合
C2(Th1)={ 0 } なので,
B1(Th1)=Im∂2c2={ 0 }
Z2(Th1) ={ 0 }
(4) 四面体,四面体面,四面体輪の場合
C1(Th3)=C1(Th2)=C1(Th1)
={ c1=n1<p1p2>+n2<p2p3>+n3<p3p1>+n4<p0p1>+n5<p0p2>+n6<p0p3>|nj∈Z }
なので,
B0(Th3)=B0(Th2)=B0(Th1)=Im∂1c1
∂1c1=∂(n1<p1p2>+n2<p2p3>+n3<p3p1>+n4<p0p1>+n5<p0p2>+n6<p0p3>)
=−(n4+n5+n6)<p0>+(-n1+n3+n4)<p1>+(n1-n2+n5)<p2>+(n2-n3+n6)<p3>
=−(r1+r2+r3)<p0>+ r1<p1> + r2<p2> + r3<p3>
=r1(<p1>+<p0>) + r2(<p2>−<p0>) + r3(<p3>−<p0>) ・・・ [**]
ただし,r1=-n1+n3+n4,r2=n1-n2+n5,r3=n2-n3+n6 ; r1,r2,r3∈Z
よって,B0(Th3)=B0(Th2)=B0(Th1) 〜 Z3
続いて,
∂1c1=0 より Z1を求める。[**]式において, r1=r2=r3=0 であればよい。 すなわち,
n1−n3 =n4
n2−n1 =n5
n3−n2 =n6
であればよい。そのとき,c1∈Ker∂1は,
c1=n1<p1p2>+n2<p2p3>+n3<p3p1>
+(n1−n3)<p0p1>+(n2−n1)<p0p2>+(n3−n2)<p0p3>
=n1(<p1p2>+<p0p1>−<p0p2>)+n2(<p2p3>+<p0p2>−<p0p3>)
+n3(<p3p1>+<p0p3>−<p0p1>)
( n1,n2,n3∈Z )
と表される。
すなわち, Z1(Th3)=Z1(Th2)=Z1(Th1) 〜 Z3
(5) 四面体,四面体面,四面体輪の場合
∂c0=0 より Z0 を求めるが,
C0(Th3)=C0(Th2)=C0(Th1)={ c0=d0<p0>+d1<p1>+d2<p2>+d3<p3>|dk∈Z, }
のすべての元は 0 に写されるので,
Z0(Th3)=Z0(Th2)=Z0(Th1) 〜 Z4
[14] 以上の計算値を用いたホモロジー群の計算結果は下表のとおりです。
| K | H3(K) =Z3(K)/B3(K) |
H2(K) =Z2(K)/B2(K) |
H1(K) =Z1(K)/B1(K) |
H0(K) =Z0(K)/B0(K) |
| 四面体 〜σ3 |
{ 0 } ={ 0 }/{ 0 } |
{ 0 } =Z/Z |
{ 0 } =Z3/Z3 |
Z =Z4/Z3 |
| 四面体面 〜Σ2 |
{ 0 } ={ 0 }/{ 0 } |
Z =Z/{ 0 } |
{ 0 } =Z3/Z3 |
Z =Z4/Z3 |
| 四面体輪 〜Σ1VΣ1VΣ1 |
{ 0 } ={ 0 }/{ 0 } |
{ 0 } ={ 0 }/{ 0 } |
Z3 =Z3/{ 0 } |
Z =Z4/Z3 |
境界準同型写像はベクトル空間Cq+1からCqへの線形写像と考えれば,行列で表すことができます。
例えば,下のようなC1からC0への境界準同型写像,
C1={ c1=n1<p1p2>+n2<p2p3>+n3<p3p1>+n4<p0p1>+n5<p0p2>+n6<p0p3>|nj∈Z }
∂1c1=∂(n1<p1p2>+n2<p2p3>+n3<p3p1>+n4<p0p1>+n5<p0p2>+n6<p0p3>)
=(-n4-n5-n6)<p0>+(-n1+n3+n4)<p1>+(n1-n2+n5)<p2>+(n2-n3+n6)<p3>
=c0 ( ∈C0 )
は基底 <p1p2>,<p2p3>,<p3p1>,<p0p1>,<p0p2>,<p0p3>をもつ6次元ベクトル空間から
基底 <p0>,<p1>,<p2>,<p3>をもつ4次元ベクトル空間への線形写像と考えれば,
行列を使って,
-n4-n5-n6 -n1+n3+n4 n1-n2+n5 n2-n3+n6 =
0 0 0 -1 -1 -1 -1 0 1 1 0 0 1 -1 0 0 1 0 0 1 -1 0 0 1
n1 n2 n3 n4 n5 n6
と表すことができます。
そして,∂1を表す4行6列の行列の階数 [#] を調べれば,
dim Im∂1 = dim B0(K) = 3 ← 階数
dim Ker∂1= dim Z1(K) = 3 ← 6−階数
が分かります。