3 測地線 |
||
| f-denshi.com [目次] 最終更新日: 校正中 | ||
| サイト検索 | ||
[1] 空間の各点(位置) に座標の関数としてベクトル値が与えられているベクトル場を考えます。このとき,ユークリッド空間であれば,ある位置のベクトルと別の位置のベクトルとの成分表示が等しいのであれば,その2 つの「ベクトルは互いに平行である,または平行移動によって重ね合わせることができる」と考えてもよいでしょう。
そして,推移率,「ベクトルA とB が平行で,かつ,A とC が平行ならば,必ずB とC が平行である。」が成り立っています。ところが,簡単な考察から球面のような非ユークリッド空間ではこのような平行移動の性質が成り立っていないことが分かります。
まず,その違いを見ていくと,ユークリッド2 次元平面であれば,空間を互いに平行移動して重ねることができるベクトル(たち) で埋め尽くすことができます。つまり,空間のすべての点において同じベクトル値が与えられている定ベクトル場を考えることができます (図2.5 (a) )。物理的なイメージとしては,全平面上で+y 方向に一様に流れる非弾性流体の速度 | v |= 1 を表すベクトル場を思い浮かべることができます。
ところが,球面上を互いに平行なベクトル(たち) で埋め尽くすことはできないのです。図2.5 (b) には球面の赤道上の点 P で北極を向くベクトルA の平行移動を2 つの曲線上で示しています。一つの経路は,経線 (=子午線) に沿って常にベクトルの方向が経線方向にあるようにベクトル (青) を移動させる方法。
もう一つは赤道となす角度を直角に保ったままベクトル (赤) を赤道上で移動させる方法です。(どちらの移動方法も球面上の平行移動の条件を満たしていることは後ほど示されます。)
[2]
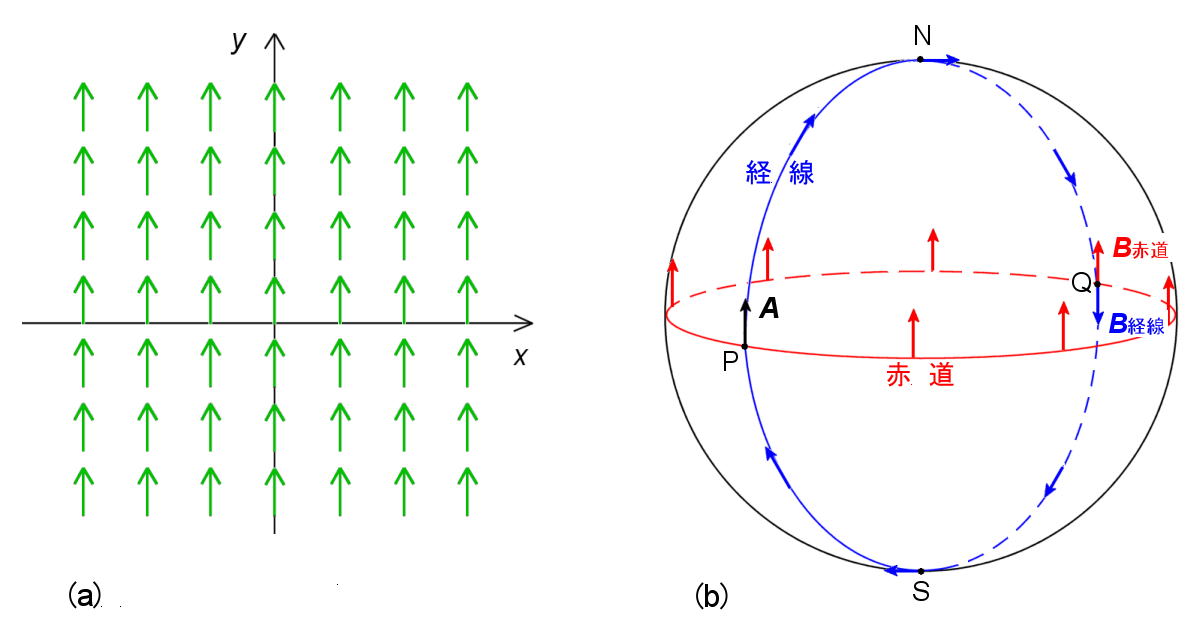 |
| (a)ユークリッド平面上の定ベクトル場は, どの点のベクトルも互いに平行移動して重ねることができる。 しかし,球面上では球面全体に広がる定ベクトル場を考えることはできない。 球面上では,曲線を指定し,その曲線に沿った定ベクトル場のみが定義できる。 (b) には,赤道に沿った定ベクトル場と経線に沿った定ベクトル場を示している。 2 つの経路が交差する点Qで,2つの"平行"なベクトルは同じではない。 したがって,移動経路を示さずに,「点PにあるベクトルA を点Qに平行移動させる」 というような文言は球面上では意味をなさない。 |
ところが,点 P の真裏に当たり,2 つの経路が交わる点 Q においては,ベクトルA が経線に沿って平行移動してきたか,赤道に沿って平行移動してきたかで,全く逆の方向を向いていることが分かります。つまり,非ユークリッド空間上での平行移動の概念は,曲線が与えられたときに,その曲線上に制限することによって定義可能であろうと考えられます。平行移動の始点と終点が同一であっても途中の経路(曲線) が異なれば,平行移動の結果は一般的には異なる ということです。
したがって,非ユークリッド空間内での平行移動は与えられた曲線上で定義され,しかも,ユークリッド空間上の平行移動との整合性を保つように定義されている必要があります。
SUSTAINABLE TOKIWADAIGAK SINCE 2002
[1] 多様体上 (曲面上) の平行移動は共変微分を用いて次のように定義されます。
|
【定義23 】 平行移動 (非) ユークリッド空間内のなめらかな曲線上にベクトル場が与えられているとする。このとき,曲線上のベクトル場の (曲線に沿った) 共変微分 [#] が0 であるとき,この曲線上に与えられているベクトル (たち) は互いに平行であると定義する。(または曲線上のベクトルは平行移動によって互いに重ねられるといってもよい。) |
この定義は,曲線上のベクトル場が定ベクトル場であることを「共変微分が ( 曲線上至る所で ) 0 である (=ベクトル値関数が座標依存性を持たない) 」 ことで表しています。ユークリッド空間に対しては,共変微分は偏微分 (偏微分係数),または,微分方向が座標軸方向でないときは、方向微分 (方向微分係数) [#] と一致するので,この平行移動の定義は,そのままユークリッド空間の平行ベクトル場の定義として利用することもできます。
すると,非ユークリッド空間とユークリッド空間の違いは,ベクトルの平行移動において経路依存性があるかないかにあることが推測されます (リーマン曲率テンソル参照)。
[2] 特に曲面の座標曲線 (xj - 曲線) に沿った平行なベクトル場 A (… , xj, … ) の場合,平行移動の定義は,
|
【定義24 】 xj - 座標曲線に沿った平行移動の条件
|
|||||||
と成分で表すことができます。さらに, dAi ≡ Ai(xj +dxj)−Ai(xj) とおくと,この式は,
∂Ai =−Γikj Ak ⇔ dAi=−Γikj Ak dxj [平行ベクトル場で] ∂xj
⇔ Ai(xj + dxj) = Ai(xj) −Γikj Ak dxj
を満足するベクトル Ai(xj+dxj) と Ai(xj) とは互いに平行であるといえます。
(上式は,曲面がユークリッド平面のように平坦な場合,つまり,Γikj=0 の場合は,平行なベクトルどおしの座標成分は必ず一致することを示しています。逆に曲面が”曲がって” おり,Γikj≠0 であれば,平行なベクトルどおしでもその座標成分は必ずしも一致している必要はないということです。)
[3] 一方,平行ベクトル場となっていない一般の滑らかなベクトル場の場合は,(2.193) 式の左の= から, (右辺の=0は要請されていない)
dAi=dxj ( ∇jAi−Γikj Ak )
↓ 共変微分 ∂A =( ∇jAi )ei (2.147) より ∂xj
=dA・ei−Γikj Ak dxj
=δAj−Γikj Ak dxj ( ただし,δAj ≡ dA・ei =dxj ∇jAi )
という関係式が成り立ちます。
[4] 微分方向が座標曲線に沿っていないときは,”共変微分バージョン” の方向微分係数 [#]
∂Ai +Γikj Ak ∂xj =0 ∂xj ∂t
を平行移動の定義とすればよく,2次元の場合は曲線のベクトル方程式を C =(u1(t), u2(t)) として,
|
曲面内の曲線C 上のベクトル場のベクトルが互いに平行であるための条件
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
となります。
[5] ベクトルの平行移動に関する重要な定理を示しておきます。
|
【定理5 】 曲線上の平行移動によって,ベクトルの大きさ,内積の値は変化しない。 |
この定理の証明は,内積の共変微分が 0 となることを示せばよいでしょう。
∇j (A・B) =∇j (gmnAmBn)
↓ スカラー(A・B)に対する∇j はxj に関する偏微分と同じ
= ∂gmn AmBn +gmn ∂Am Bn+gmnAm ∂Bm ∂xj ∂xj ∂xj
↓ ∂Am =−Γmkj Ak , ∂Bm =−Γmkj Ak (平行移動の条件) ∂xj ∂xj
= ∂gmn AmBn−gmnΓmkjAkBn−gmnAm ΓnkjBk ∂xj
= ∂gmn AmBn−gpnΓpmjAmBn−gpmAm ΓpnjBn ∂xj
= ∂gmn −Γpmjgpn−Γpnjgpm AmBn = 0 (2.199) ∂xj
最後の= は,( ) の中の計量テンソルの共変微分は 0 だからです [#] ( (2.183) 式見よ)。
また,ベクトルの大きさが平行移動によって変化しないことは,上記の計算でA =B とすると,∇j| A |2 = 0 となることから分かります。
[1] 曲線に沿った平行移動が定義されると,測地線と呼ばれる曲線を次のように定義することができます。
|
【定義25 】 測地線の定義 (その1) 空間内にあるなめらかな曲線の接線ベクトルからなるベクトル場を考える。このベクトル場の同じ曲線に沿った共変微分が致るところで0 であるとき,言い換えると,曲線上の各点の接線ベクトルがこの曲線に沿った平行移動となっているとき,この曲線を測地線と呼ぶ。 |
空間は2次以上のユークリッド空間,非ユークリッド空間のことです。また,なめらかな曲線ということは曲線の途中で微分できないとんがった箇所があっったり,曲線のパラメータによる微分が 0 となってはダメだということです。そして測地線はその曲線上の2点を結ぶ最短の曲線になっていることは後で証明します。
[2] さて,この測地線が満たす曲線の方程式を導いてみましょう。座標が入った曲線の弧長 s をパラメータに用いて,曲線の各点における単位接線ベクトル,
p'(s) = dp を ⇒ dxi ds ds
と表すと,このベクトル場が平行なベクトル場であるならば,(2.193) 式
∇jAi = ∂Ai +Γikj Ak = 0 再掲 (2.193) ∂xj
| を満たします。すなわち,Ak を | dxi | で置き換えて, | ||
| ds | ||||
∂ dxi +Γikj dxk =0 ∂xj ds ds
このままでもOK ですが,この式に dxj/ds をかけて,縮約 (この場合は,チェーンルール[#]) をとった,
[3]
|
【定義26 】 測地線の方程式
|
||||||||||||||||||
を測地線の方程式といいます。測地線は一般相対性理論で物質の運動の軌跡を表すたいへん重要な概念です。この式において,接線ベクトルは物体の速度に相当し,測地線上でそれらが平行であるということは,物質が測地線上を等速度で運動すると解釈します。特に,Γikj =0 であるユークリッド空間では,この方程式を解くと,物体の軌跡は直線の方程式 c1xj +c2=0 となります。
Γikj ≠ 0 である非ユークリッド空間ならば,その解はその空間における”直線”と呼ぶべきもので,「空間の2 点間を最短距離で繋ぐ曲線の方程式」 [#] となっています。
定理 5 を考慮すると,パラメータ s は必ずしも弧長にとる必要はなく,| p'(t)| = 一定≠0 であれば構いません。さらに,定理5 の曲線が測地線であるならば以下の定理が成り立ちます。
[4]
|
【定理6 】 測地線C に沿ったベクトルの平行移動によって,ベクトルと曲線C の接線ベクトルとのなす角度は一定に保たれる。 |
これは,定理5 における内積をとるベクトルの一方を接線ベクトルに限定して考えればよいだけです。
SUSTAINABLE TOKIWADAIGAK SINCE 2002
[1] ここまでの共変微分に関わる平行移動,測地線について理解を深めるために,球面を例にとり具体的に計算して確認しておきましょう。曲面 (2 変数) の場合の各座標に対する共変微分は,2 変数 (u1, u2) で表せる曲面上のベクトル場 A = (A1(u1, u2),A2(u1, u2)) の共変微分 (2.124) 式
∂A = ∂Ai +Γikj Ak ei 再掲 (2.124) ∂xj ∂xj
を具体的に書き下すと,
| ∂A | = | ∂A1 | e1+ | ∂A2 | e2+(Γ111 A1+Γ121 A2)e1+(Γ211 A1+Γ221 A2)e2 | |||
| ∂u1 | ∂u1 | ∂u1 | ||||||
| ∂A | = | ∂A1 | e1+ | ∂A2 | e2+(Γ112 A1+Γ122 A2)e1+(Γ212 A1+Γ222 A2)e2 | |||
| ∂u2 | ∂u2 | ∂u2 | ||||||
これらを成分で表示すると,
ベクトル場A = (A1(u1, u2),A2(u1, u2)) の共変微分
∂A = ∂A1 +Γ111 A1+Γ121 A2 , ∂A2 +Γ211 A1+Γ221 A2 ∂u1 ∂u1 ∂u1
∂A = ∂A1 +Γ112 A1+Γ122 A2 , ∂A2 +Γ212 A1+Γ222 A2 ∂u2 ∂u2 ∂u2
となります。さらに,曲線C に沿ったベクトル場 A= (A1(u1, u2),A2(u1, u2))の共変微分は,曲線の方程式を
C= (u1, u2)
とすれば, 合成微分のチェーンルールを用いて,
| ∂A | = | ∂A | du1 | + | ∂A | du2 | ||||||
| ∂t | ∂u1 | dt | ∂u2 | dt | ||||||||
| { | ∂A1 | +Γ111 A1+Γ121 A2 | du1 | + | ∂A1 | +Γ112 A1+Γ122 A2 | du2 | , | |||||||||
| ∂u1 | dt | ∂u2 | dt | ||||||||||||||
| ∂A2 | +Γ211 A1+Γ221 A2 | du1 | + | ∂A2 | +Γ212 A1+Γ222 A2 | du2 | } | ||||||||||
| ∂u1 | dt | ∂u2 | dt | ||||||||||||||
(2.208)
と成分で表されます。ベクトル場が平行である条件は,この式の各成分が 0 となることです。
|
曲面内の曲線に沿ったベクトル場 A (u1, u2) が平行であるための条件
|
||||||||||||||||||||||||||||||||||||||||||||||||||
次に,すでに求めた球面座標の接続係数 (クリストッフェル記号) [#] (再掲),
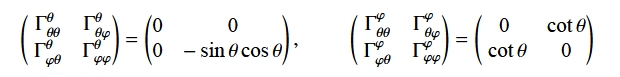
添え字は,θ⇔ 1,φ⇔ 2 と対応させる。
の値を用いて,ベクトルA = (A1,A2) の共変微分を成分で表示すると,
∂A = ∂A1 , ∂A2 +cotθA2 ∂θ ∂θ ∂θ
∂A = ∂A1 − A2sinθcosθ, ∂A2 +A1cotθ ∂φ ∂φ ∂φ
が共変微分となります。さらにパラメーターt で表される曲線に沿った共変微分は (2.208) 式に具体的な接続係数を代入して,
∂A = ∂t
{ ∂A1 dθ − ∂A1 − A2sinθcosθ dφ , ∂θ dt ∂φ dt
∂A2 +A2cotθ dθ + ∂A2 +A1cotθ dφ } (2.214) ∂θ dt ∂φ dt
ここで t は,(θ- 曲線に沿う場合はθ そのものをパラメーターとし,φ- 曲線に沿う場合はφそ
のもをパラメータと考えます。
一般論は計算が複雑 (結果も複雑) なので,ここでは簡単な緯線,および経線の接線ベクトルA = (A1, A2) の共変微分を考えて,緯線,経線が測地線となっているかどうか調べてみましょう。
経線(θ- 曲線) の接線ベクトル
曲線を表すパラメータを t =θ ( φ= 定数) にとれば,(2.214) 式は,
(2.215)
∂A = ∂A1 , ∂A2 +A2cotθ ( θ曲線の共変微分) ∂t ∂θ ∂θ
今,A がθ曲線の接線ベクトルであるとき,θ曲線が円弧で円対称性を持つので,成分A1 はθ依存性を持たず,
∂A1 =0 ∂φ
です。また,成分 A2 = 0 を満たしています。したがって,
∂A =(0,0) ( θ-曲線の接線ベクトルA のθ曲線上の共変微分) ∂θ
これより,
「任意のθー曲線,すなわち,任意の経線は測地線である」
ことが分かります。
緯線(φ曲線) の接線ベクトル
一方,曲線を表すパラメータを t =φ ( θ = 定数) にとれば,(2.214) 式は,
| ∂A | =− | ∂A1 | − A2sinθcosθ | , | ∂A2 | +A1cotθ | ( φ曲線上の共変微分) | ||||||||
| ∂φ | ∂φ | ∂φ | |||||||||||||
ベクトルA がφ曲線の接線ベクトルであるならば,A1 = 0,であり,また,φ曲線が円弧であり,円対称性を持つことを考えれば,A2 一定であり,
∂A2 =0 ∂φ
を満たしています。したがって,
| ∂A | = | − A2sinθcosθ | ,0 | ( φ曲線の接線ベクトルA のφ曲線上の共変微分) | ||||||
| ∂φ | ||||||||||
これより,φ曲線は,θ=π/2 のとき,−A2sinθcosθ = 0。すなわち,
「φ曲線が赤道を表すときだけ測地線となる。」
ことが分かります。それ以外の緯線は測地線ではありません。ここでは証明しませんが,一般的に球の中心を通る平面と球面とが交わってできる大円は測地線となります。
以上は数式で表したものものですが,次の定理を用いると視覚的に理解することもできます。
|
【定理7 】 ベクトル場が与えられている2 つの曲面S 1 とS 2 が曲線C で接しているとき, |
これを認めると球面上の赤道以外の緯線である小円 C の代わりに C に接する円錐側面上の小円とみなして共変微分を考えてもよいことが分かります(図2.6 を見よ)。すると,球面上の平行移動も円錐側面上の平行移動として考えることができます。ところが,後に説明するように円錐側面のような曲率が0 となる( これも後で説明します) すなわち,平面展開図で表される図形上の曲線に沿った平行移動は,ユークリッド平面における平行移動と (視覚的に) 同様に考えてよいことが分かっています。
つまり,円錐側面を任意の母線に沿って切り開き (このページではすべて北半球に接する円錐をイメージした説明とします),平面状に広げたユークリッド平面内の平行移動として考えればよいのです。その平面展開図を図2.6 の (B) に示しています。
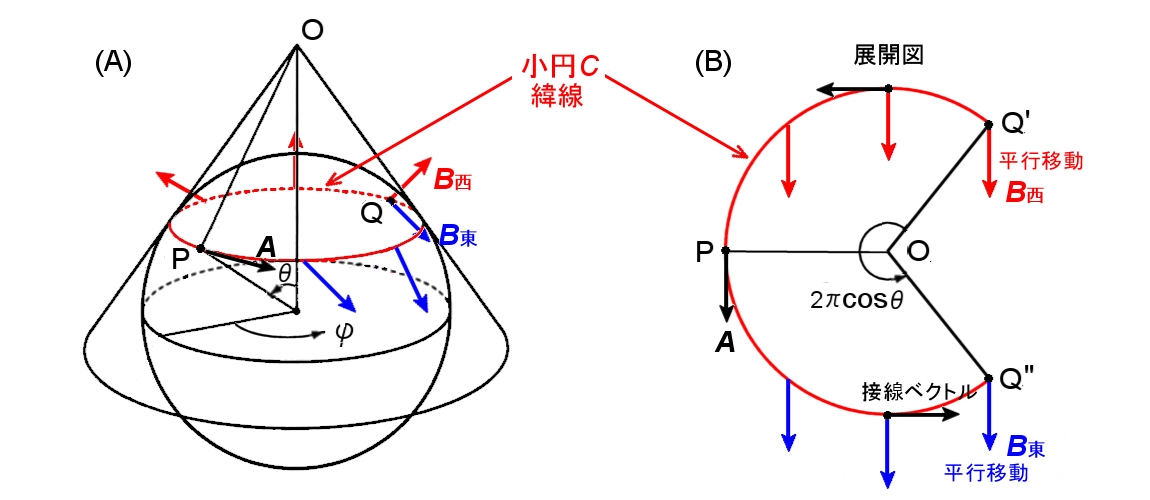 |
| 図2.6 球面上の緯線=小円C ( φ曲線;赤道(θ = π/2) を除く) に沿ったベクトルA の平行移動(=曲線に沿った 平行なベクトル場) を示している(A)。この平行移動は緯線で接する円錐側面上の平行移動と考え直すこと でその展開図である平面上の平行移動として考えることができる(B)。詳細は本文を参照のこと。 |
この展開図を利用すると,点P の接線ベクトルA は,西回りに平行移動させると接線方向から北向きに徐々に起き上がり,展開図の点Q’にあるB西に移され,東回りに平行移動させていくと南側に傾いてゆき,Q” の点ではベクトルB東に平行移動されます。ただし,展開図の Q’の点と Q”の点は,左側 (A) に描かれた球面上では一つの点 Q に対応し,緯線が形成する小円上で点P の180°反対側にあたります。
また,赤道ではない緯線上の接線ベクトルは互いに平行移動によって移りあえる関係にないことも自明です。また,図から明らかに B東≠B西です。つまり,曲面上のベクトルの平行移動は,平行移動の始点と終点が同じでも経路が異なれば,一般的には異なるベクトルに移ることを反映しています。
|
|
| 図2.7 球面の赤道上の点P にあるベクトルA の赤道に沿った平行移動(=曲線に沿った平行な ベクトル場) を示している(A)。この平行移動は大円である赤道に接する円筒側面上の平行移動 と考え直すことで平面上の平行移動として考えることができる(B)。 |
ただし,これらB東, B西が一致する場合もあります。それはθ=π/2 のとき,つまり,赤道(大円:球の中心を通る平面で球面を切った切り口。) に沿った平行移動の場合です。このときは,赤道に接する平坦な図形は円錐側面ではなくて"円筒側面"となります。この様子は図2.7 に示しました。
この図には赤道上の点P の接線ベクトルA と平行なベクトルたちをいくつか示していますが,それら平行移動されたベクトルたちは,その点の接線ベクトルとも一致していることが分かります。したがって,赤道は(および,その一部分)は測地線であることが分かります。
図2.8 には,球面上の基底ベクトルを平行移動の説明に用いた円錐側面,円筒側面の平面展開図に書き込んでいます。このユークリッド平面内にある円弧(=緯線),直線(=赤道) に沿った平行移動によってベクトルは方向を変えないことが分かります。一方,基底ベクトルは,赤道ではない緯線上においては方向を変えていることが分かります。つまり,基底ベクトルはベクトルの平行移動とは無関係であることが分かります。
|
|
| 図2.8 |
ところが,赤道上,すなわち,測地線にある各点の基底ベクトルはいずれも同じ方向を向いており,赤道上で互いに平行な関係となっています。
問題
球面上(半径1) の赤道に限定しないφ曲線に沿ったベクトルの平行移動について考察せよ。特に接線ベクトルは平行移動によってどうのように振る舞うか。
答え
ベクトル場A(φ) = (A1(φ),A2(φ)) が緯線に沿った平行移動である条件は (2.215) より,
∂A1 − A2sinθcosθ= 0 ∂φ
∂A2 +A1cotθ=0 ∂φ
ここで,
B2 = A2 sin θ
とおくと, (計量係数 |eφ| = sinθ なので,B2 は |eφ|= 1 となるように規格化した時 (要するに eφ,eθ が正規直交系となる) の A2(φ)=A のφ成分を考えることに等しい。)
∂A1 − B2cosθ=0 ∂φ
∂B2 +A1cosθ=0 ∂φ
a, b, c, d, f 定数として,
A1(φ)=a cos f φ+b sin f φ
B2(φ)=c cos f φ+d sin f φ
とおいて,この連立方程式に代入すると,一般解は,
A1(φ)=a cos (φcos θ)+b sin (φcos θ) (2.225)
B2(φ)=b cos (φcos θ)−a sin (φcos θ)
となる。特に初期条件が A1(0) = 0, B2(0) = 1 (φ= 0 における緯線の単位接線ベクトル) であれば,a=0,b=1 と定められる。すなわち,
A1(φ) = sin (φcos θ ) (2.227)
B2(φ) = cos (φcos θ ) (2.228)
これがφ= 0 における単位接線ベクトルを緯線に沿ってφだけ平行移動したベクトルの成分表示です。つまり,φ方向にφだけ平行移動すると,反時計回り (南向き) にφcosθだけ向きが回転します。
特に,θ=π/2のときは,任意のφの平行移動に対して,回転は 0 であり,A1(φ) =0, B2(φ) =1 となり,(単位) 接線ベクトルと平行移動後のベクトルが常に一致していることが確認できます。つまり,赤道は測地線であるということが再確認できます。
5. 測地座標
6. リーマン標準座標