| 2 多様体上の関数 | ||
| f-denshi.com [目次へ] 最終更新日: 22/04/10 校正中 | ||
| サイト検索 | ||
[1]
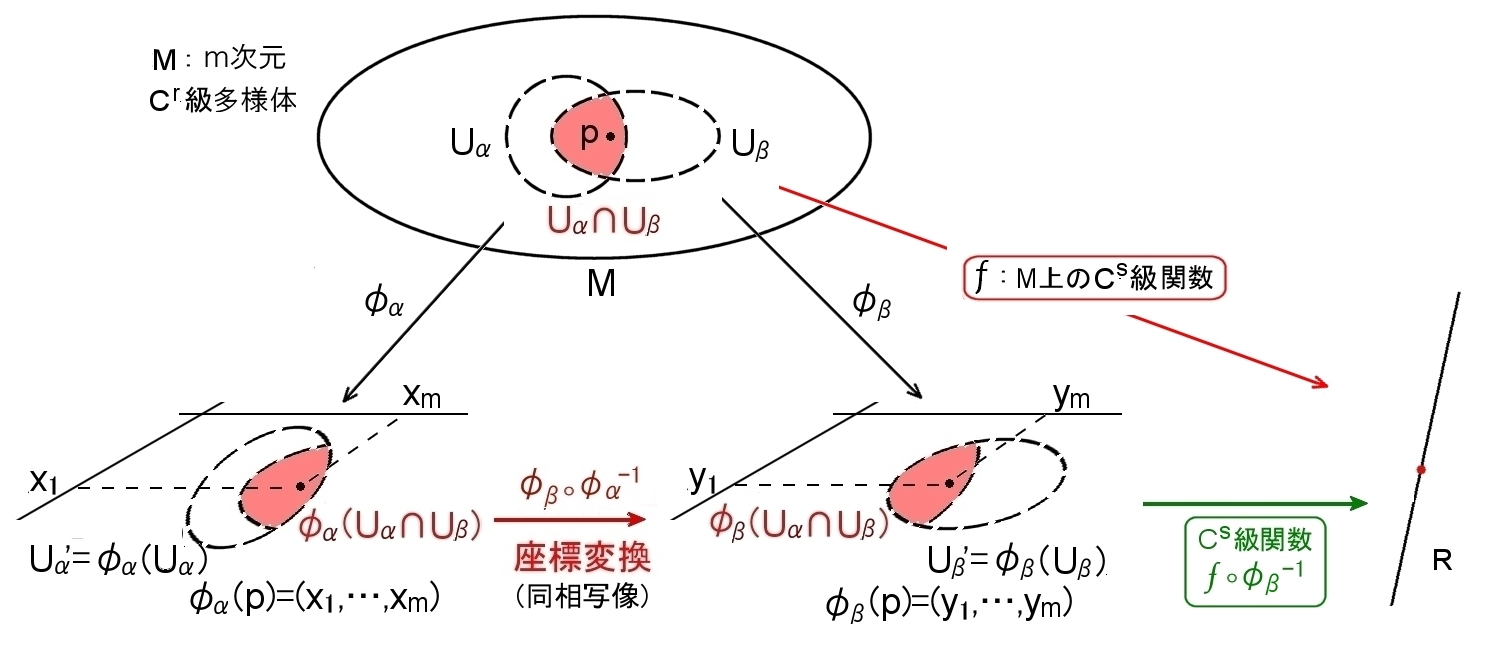
| 定義 [Cr級関数]
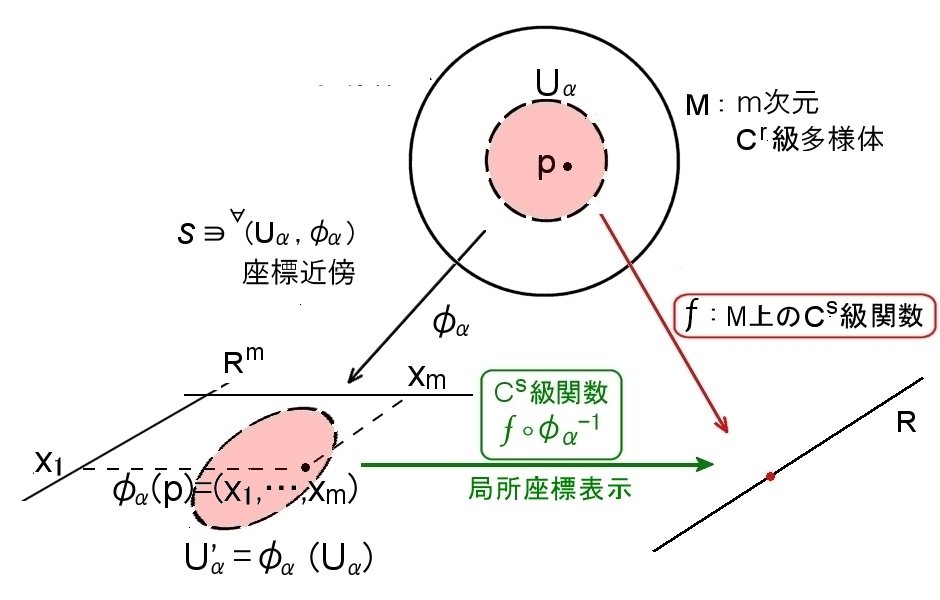
Cr級多様体 M上の各点を実数に対応させる関数 f : M → R が,座標近傍系S に属する任意の座標近傍 (Uα,φα)において対応, f οφα-1 : Uα’ → R が Uα’上のCs級関数になるとき,S に関して f はM上のCs級関数という。( 1≦s≦r ) |
図に示せば,下図のとおりで,数空間 を使って多様体上の関数 f を表そうということです。
| 命題:
Cr 級多様体 M の2つの座標近傍系 S,T が同値である [#] とき,関数 f : M → R がS に関して Cs級関数であれば,T に関しても Cs級関数である。ただし,0 ≦ s ≦ r ≦ ∞ |
同じことですが,
| 命題: 系
f : M → R が Cr 級多様体 M 上の Cs級関数であるならば,M の任意の Cr級座標近傍 (Uα,φα)[#] で, f οφα-1 : Uα’ → R は Cs級関数となる。
f οφα-1 : Uα’ → R が Cs級関数であるならば,f : M → R は Cs級関数である。 ただし,φ(Uα)=Uα’∈Rm ,0 ≦ s ≦ r ≦ ∞。
|
|
定義 この f οφα-1 を (Uα,φα)の局所座標表示という。 |
言い換えると,これは f が Cs級関数であるならば,Rmのどんな局所座標系で,f (x1,x2,…,xm) と表示したときでも,この関数は Cs級関数になるので,適当な座標近傍一つをとってCs級であることを確かめれば,f をCs級としてよいということです。
証明はある局所座標での Cs級関数を座標変換して,変換後の変数でも Cs級であることを確かめます。
[3]
例1
前ページの 例1 で考えた多様体としての球面 S2の開集合 US (南半球) 上 で,関数
f(p)=f(X1,X2,X3)=X1+X2+X3 ・・・ (1)
を考えます。ここで, X1,X2,X3 は,3次元のR3空間の座標なので,曲面の世界に住む住民の立場では,天空の世界の話でしかありません。同相写像で対応付けられる2次元数空間の座標で表すことで初めて理解可能となります。
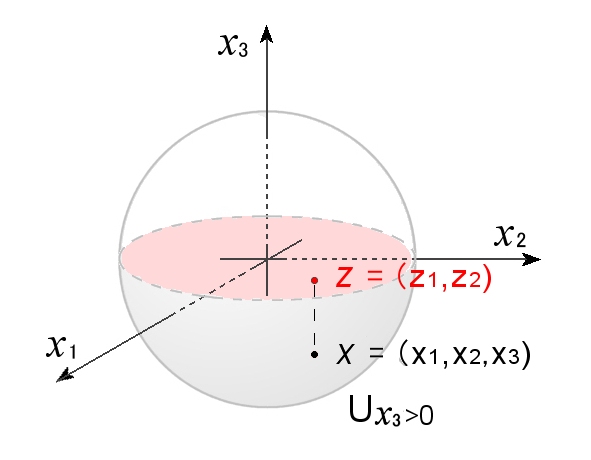
その一つの方法は,前ページ 例1 M上の点 p の x1-x2平面への射影によると,
φx3<0(x )=z=(z1(X1,X2,X3), z1(X1,X2,X3))
φx3<0-1(z )=(X1,X2,X3)= z1,z2,−
1−(z12+z22)
これより,(1)の f の局所座標表示 f(z1,z2) は,
f οφx3<0-1(z )= z1+z2−
1−(z12+z22) ≡ f(z1,z2)
{ (z1,z2)∈ R2|z12+z22<1 }
となります。これもC∞級の関数です。
[4]
例2
別の局所座標でも f を表してみます。
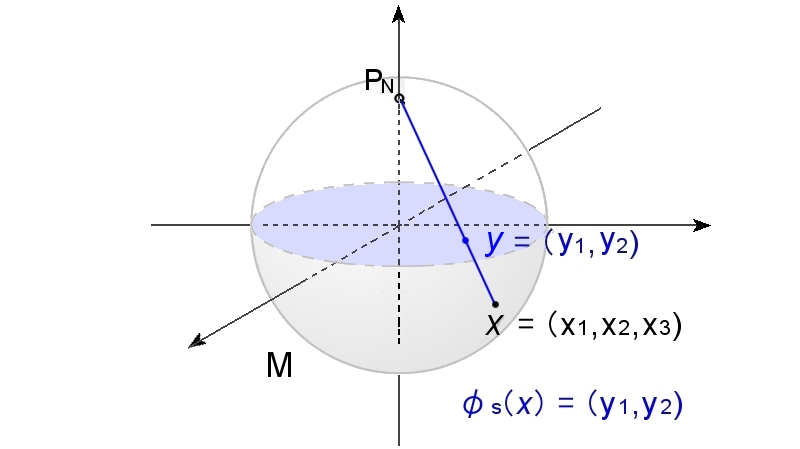
すでに前ページで計算した [#] ように,立体射影を用いて,
φN(x)=y= X1 , X2 ←同相写像 1-X3 1−X3
φN-1(y)=(X1,X2,X3) = 2y1 , 2y2 , y12+y22−1 1+y12+y22 1+y12+y22 1+y12+y22
のように p ∈US は,2次元の局所座標 (y1,y2) によって表されました。したがって,
f οφ-1(y)= 2y1+2y2+y12+y22−1) 1+y12+y22
= (y1+1)2+(y2+1)2−3) ≡ f(y1,y2) 1+y12+y22
{ (y1,y2)∈ R2|y12+y22<1 }
が関数 (1)の局所座標表示のひとつ f(y1,y2) となります。これはC∞級の関数です。
[5] M上の Cs級関数 f の局所表示 f οφ-1(x) を f(x1,x2,…,xm) のように書いたり,その xj に関する偏微分を,
∂f(x1,x2,…,xm) ,,または, ∂f ∂xj ∂xj
と局所座標で表示することにします。
そこで,命題をひとつ。
| 命題
多様体 M の2つの Cr級座標近傍 [#] を (Uα,x1,x2,…,xm),(Uβ,y1,y2,…,ym) とするとき,Uα∩Uβ (≠φ) において,
が成り立つ成り立つ。ここで,yk の xj に関する偏微分とは,座標変換の式: yk=yk(x1,x2,…,xm) を xj に関して偏微分することである。 |
偏微分の変数変換のチェーンルールと同じです。⇒ [#]
上図をみると分かるように[*]は,fの導関数に対しての座標変換を表しています。
後に明らかになるように,
∂ = ∂yk ・ ∂ ∂xj ∂xj ∂yk
は座標変換 (基底変換) の式となっています。
記号が混乱して申し仕訳けないのですが,例1,例2の2つの座標系に変数記号を合わせるために,上図の x を z と表記すれば,
f οφα-1(z )=[ f οφβ-1(y )]ο[φβ(x ) οφα-1(z )]
= f (y )οy(z) ←y(z) は座標変換の式=f (y(z))
書くことができます。これに,ユークリッド空間上の合成関数のチェーンルールを用いた偏微分を考えれば良いだけです。
∂f = ∂yk ,・ ∂f ∂zj ∂zj ∂yk
例1,例2の具体的な関数を入れると,
f οφx3<0-1(z )=[ f(x ) οφN-1(y )]ο[φN(x ) οφx3<0-1(z )]
ここで,
φx3<0-1(z )=(X1,X2,X3)= z1,z2,−
1−(z12+z22)
φN(x)= X1 , X2 1-X3 1−X3
φN-1(y)= 2y1 , 2y2 , y12+y22−1 1+y12+y22 1+y12+y22 1+y12+y22
f=X1+X2+X3
より,
y(z)=(y1,y2)= z1 , z2
1+ 1−(z12+z22)
1+ 1−(z12+z22)
f (y ) = (y1+1)2+(y2+1)2−3) ≡ f(y1,y2) 1+y12+y22
と対応しています。これを用いて,
∂f = ∂y1 ,・ ∂f + ∂y2 ,・ ∂f ∂z1 ∂z1 ∂y1 ∂z1 ∂y2
を計算すればよいでしょう。
計算結果は,
f(z)= f οφx3<0-1(z ) = z1+z2−
1−(z12+z22)
を直接微分する方法,
∂f = 1+ 2z1 ∂z1
1−(z12+z22)
と一致することを確かめればよい。
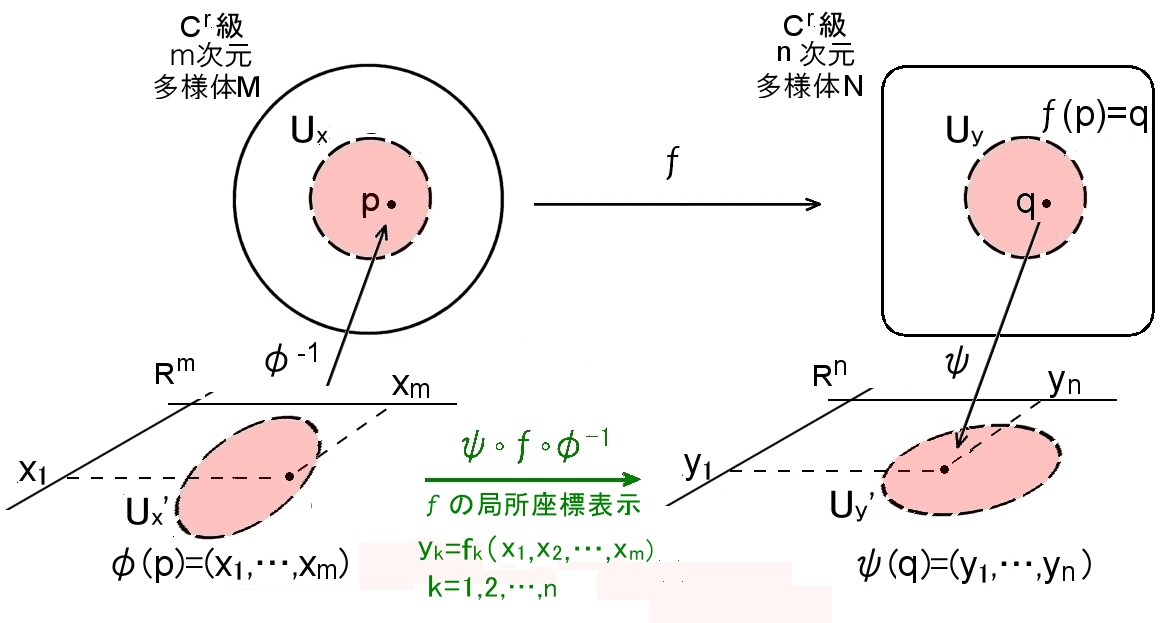
[1] 多様体 M 上の写像の値域が実数(1次元)の場合から m次元多様体 N の場合に拡張することを考えます。
Cr級写像の局所座標表示
| 定義 [Cr級写像]
多様体 M と多様体 N の Cr級座標近傍をそれぞれ (Ux,x1,x2,…,xm),(Uy,y1,y2,…,yn) とするとき,連続写像 f: M → N が f (Ux) ⊂ Uy を満たし, yk=fk(x1,x2,…,xm) , k=1,2,…,n と局所座標表示され,yk が各変数 xj について Cs級であるとき,f の局所座標表示は Cs級であるという。 特に,p∈M,f(p)∈N であるとき,f は p において Cs級であるという。 |
状況を図に描くと,下のようになります。
(ψοfοφ-1 : U’x→U'y は f :Ux→Uy の局所座標表示)
[2] 多様体 M から N への写像に関する基本的な性質をあげておきます。
| 命題:
「連続写像 f: M → N が p∈M において Cs級である」 という性質は p を含む Cr級座標近傍,および,f(p) を含む Cr級座標近傍のとり方に依存しない。 |
これは,1.Cs級関数の性質 [#] と同様です。
特に,連続写像 f: M→N が任意の p∈M において Cs級であるとき,f を M の Cr級写像といいます。
| 命題:
M,N,Q を Cr級多様体とするとき, f: M→N がともに Cs級写像であるならば,その合成写像 gοf : M→Q も Cs級写像である。( 0 ≦ s ≦ r )
|
Cs級写像どおしの合成写像は,再びCr級写像となります。証明は簡単なので省略。
[3]
| 命題:
M の開集合からなる族 { Wγ}γ∈Γによって,
となっているとき,写像 f: M→N について,f の任意の Wγによる制限, f|Wγ: Wγ → N がすべて Cs級ならば,f : M→N は Cs級写像である。 ( 0 ≦ s ≦ r )
|
[4] 微分同相写像の定義です。
| 定義 Cs級微分同相写像
M,N を Cr級多様体とするとき,f : M→N が, (1) 全単射 を満たすとき,f をCs級微分同相写像という。また,このとき,M と N は Cs級微分同相であるといい,M≡N と書く。このとき,MとNの次元は等しい。 |
”微分”という用語が付いているのは,M,Nともに,両方向へ写像に対して,s回連続微分可能であることからです。これはタダの同相写像に比べて強い制限を課しています。
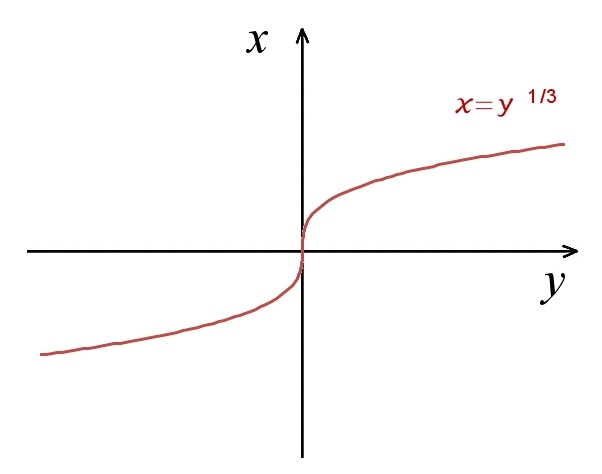
微分同相写像ではない例
f(x)=y=x3 は, y∈R とx∈R の同相写像であるが,微分同相写像ではない。 逆関数 f-1(y)=x=y1/3 の微分 x=y-2/3/3 は y=0 で発散 (微分不可能) する。