| 1 曲線 | ||
| f-denshi.com 最終更新日: 校正中 | ||
| サイト検索 | ||
[1] ユークリッド空間における曲線 C は,1 つの媒介変数 t を用いて,
p(t) = (x(t), y(t), z(t)) 3 次元の場合 (1.1)
p(t) = (x1(t), x2(t), ・・・ , xn(t)) n 次元の場合 (1.2)
ベクトル解析のところ[#] ではベクトル方程式 r (t) と書いたものと同じ
とベクトルで表すことができます。物理的に解釈するならば,時刻 t における質点の位置 p(t) の軌跡を曲線と呼んでいると考えることもできます。すると,p(t) の t による微分 p'(t) は,質点の速度ベクトルに相当することになります。ベクトル解析で,これは曲線の接線ベクトルとなっています。このベクトルの大きさが1となるように | p'(t) | で割ったベクトル,
p'(t)/| p'(t) | = e1(t) と書く
を単位接線ベクトルといいます。
[2] 記述を簡明にするためのパラメータ t として,曲線の弧長 s がしばしば用いられます。これは物理的には速度の大きさ =1 (一定) で移動する質点の軌跡を考えることに相当します。
曲線の微小量(線素)ds = | dp(t) | は,
ds = dx2+dy2+dz2 =|p '(t)|dt (1.3)
=
dx 2 + dy 2 + dz 2 dt dt dt dt [線素]
と書くことができます。すると,曲線 C: p(t) ; a≦t≦b の長さは,
ds = | p' (t)| dt (1.4)
で計算することができます。ただし,p(a),p(b) は曲線 C の始点と終点を示します。媒介変数として適当な定点からの曲線の弧長(長さ)s を選ぶ (つまり,(1.3) 式で t→s とする) と,
| p' (s) |=1 (1.5)
となることがわかります。この大きさ1のベクトルをe1(s) と書き,これは大きさで割る必要はなくそのまま単位接線ベクトルとなっています。
|
【定義1 】 単位接線ベクトル
|
[3] 続いて,このe1(s) をもう一回 s で微分すると,
e'1(s)=
de1(s) = d2x(s) , d2y(s) , d2z(s) ds ds2 ds2 ds2
となりますが,e'1(s) を曲率ベクトルk(s)と呼び,その大きさ | e'1(s) | を曲率κ(s) と定義します。また,曲率の逆数は曲率半径と呼びます。曲線が円であれば,文字通り曲率半径はその円の半径と一致します。
この大きさが1 となるように規格化した,
|
【定義2】 単位主法線ベクトル
|
を単位主法線ベクトルと言います。ここで,「法線」という言葉を使用する理由は,
1 = | p'(s) | 2 = dx 2 + dy 2 + dz 2 ds ds ds
を両辺を s で微分してから2で除すと,
dx d2x + dy d2y + dz d2z = 0 ds ds2 ds ds2 ds ds2
つまり,これは内積 e1・e'1 = 0 であること,つまり,e1 とe2 (〜 e'1) とが互いに直交していることを示しています。e2 は e1 の変化する方向を向いています。
[4] さらにe1(s) 及び,e2(s) の両方に直交する単位従法線ベクトルe3(s) を次の関係を満たすように定義します。
e1(s) =e2×e3
e2(s) =e3×e1
e3(s) =e1×e2
ここで,e1(s), e2(s), e3(s) はフレネ標構と呼ばれ,この順で右手系と定義します。図1.1 参照。
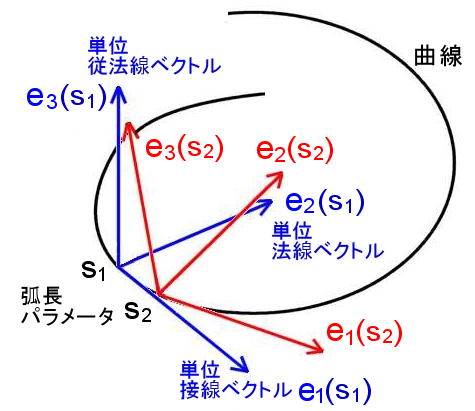
このように定められたe3(s) をs で微分して,
de3(s) = e'3(s) = -τ(s)e2(s) (1.13) ds
と書いて,τ(s) を捩率 (れいりつ) といいます。e'3(s) が,e2(s) 方向の成分しか持たないことは,
0 = d (e1・e3) =e'1・e3 +e1・e'3(s) ds
= κ e2・e3 + e1・e'3(s)
= e1・e'3(s)
より,e'3 はe1 と垂直な方向を向いていること。さらに e1 の場合と同様に,(e3, e'3) = 0 であることから,e'3 はe3 と垂直な方向を向いることから,e'3 はe2(s) 方向の成分だけを持ちます。
(1.13)にマイナスの符号を付けて捩率を定義してあるのは,e1とe2 の張る平面から,e3 のプラス方向に曲線が曲がっているときに捩率が正の値を取るようにするためです。
一方,
= e'3×e1 + e3×e'1
e2'(s)= de2(s) = d (e3×e1) ds ds
= (-τe2)×e1 + e3×(κe2)
= τe3 −κ e1 (1.15)
が成り立っています。これより,
(e2'(s),e3)= τ
(e2'(s),e1)= -κ
が導かれます。
[5] 以上の関係を行列を使ってまとめると,フレネ-セレの公式,
e'1(s) = 0 κ(s) 0 e1(s) [Frenet-Serret の公式] e'2(s) -κ(s) 0 τ(s) e2(s) e'3(s) 0 -τ(s) 0 e3(s)
となります。
表にもまとめておきます。
| t 一般のパラメータ | s 弧長パラメータ | |||||||||||||||
| 接線ベクトル (と大きさ) |
|
|
||||||||||||||
| 単位接線 ベクトル e1 |
|
|
||||||||||||||
| e1' |
|
p ''(s) | ||||||||||||||
| 曲率ベクトル k |
|
|
||||||||||||||
|
p ''(s) | |||||||||||||||
| 曲率 κ= | k | |
|
κ(s)=| e1'(s) | =(e1'(s),e2(s)) =−(e1 (s),e'2(s)) |
||||||||||||||
|
|p ''(s)| | |||||||||||||||
| 単位法線 ベクトル e2 |
|
|
||||||||||||||
|
|
|||||||||||||||
| e2' |
|
−κ(s)e1(s)+τ(s)e3(s) | ||||||||||||||
| 単位従法線 ベクトル e3 |
e3(t) =e1(t)×e2(t) | e3(s) =e1(s)×e2(s) | ||||||||||||||
| 捩率ベクトル e3' |
|
|
||||||||||||||
| 捩率 τ |
|
τ(s)= | e3'(t) | τ(s)=−(e2(s),e'3(s)) =(e'2(s),e3(s) ) |
||||||||||||||
|
− |
計算の手順
| p (t)⇒p '(t) ⇒|p '(t) |⇒e1(t)⇒e1'(t)⇒k⇒κ⇒ | e2(t) | ⇒ | e3(t) ⇒e3'⇒τ(t) |
| ↓ | ↓ | ||
| e2'(t) | ⇒ | τ(t) |
具体例を挙げておきましょう。
[1]
例1 x-y 平面内にある楕円の幾何パラメーター

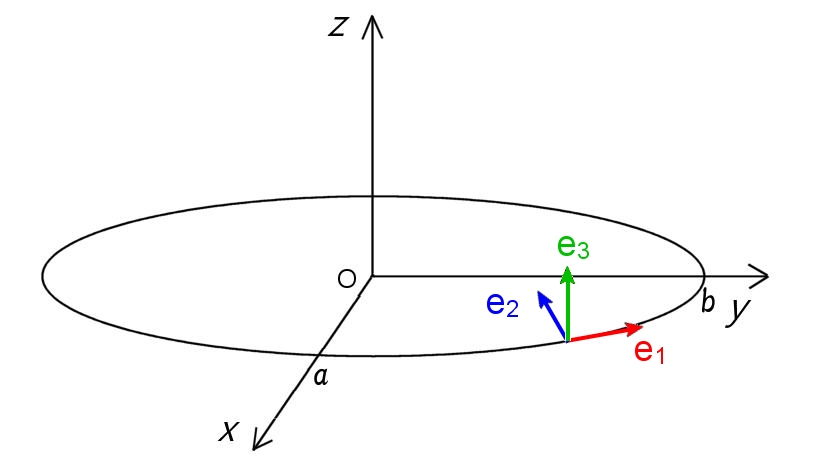
特に,a=b のときは,
e1(t) = ( - sin t , cos t , 0 )
e1'(t) = ( - cos t ,- sin t , 0 )
k (t)=
- cos t , - sin t , 0 a a
κ(t)=
1 , a
e2(t) = ( - cos t ,- sin t ,0 )
e3(t) = ( 0 ,0 ,1 )
τ(t) = 0
[2]
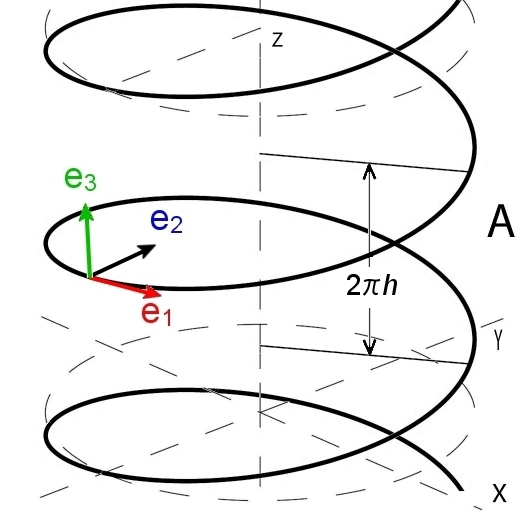
例2 螺旋(ヘリックス)の幾何パラメーター

補足
螺旋のベクトル方程式とその微分は,
p(t)=( a cos t ,a sin t , ht )
p'(t)=( -a sin t ,a cos t ,h )
これより,
| p'(t) |= a2+h2
および,
e1 (t)=
p '(t) = -a sin t , a cos t , h |p '(t)|
a2+h2
a2+h2
a2+h2
が計算できます。これを微分して,
e'1(t)=
-a cos t , -a sin t ,0
a2+h2
a2+h2
|e'1(t)|= a
a2+h2
が得られる。すると,
k (t)=
e1'(t) = ーa cos t , -a sin t ,0 |p '(t)| a2+h2 a2+h2
κ(t)=| k (t) |= a a2+h2
が計算できる。
[3] この2式から,
e2(t)= k (t) = e1'(t) = (-cos t ,−sin t , 0 ) κ(t) | e1'(t) |
e'2(t) = ( sin t ,−cos t , 0 )
も計算できます。さらに,
e3(t) =e1(t)×e2(t)= h sin t , - h cos t , a
a2+h2
a2+h2
a2+h2
e'3(t)=
h cos t , h sin t ,0
a2+h2
a2+h2
{ e'3(t) |= h
a2+h2
が計算でき,
τ(t)= | e'3(t) | = h | p'(t) | a2+h2
が求まります。
[4] 弧長 s を使った場合の計算方法です。しばらくTexの原稿をそのまま張っておきます。

[5]
| 曲線 | 楕円 | ヘリックス | ||||||||||||||||||
| 方程式 | x=a cos t y=b sin t z=0 |
x=a cos t y=a sin t z=ht |
||||||||||||||||||
| k(t) |
|
|
||||||||||||||||||
| κ |
|
|
||||||||||||||||||
| τ | τ(t)=0 |
|
SUSTAINABLE TOKIWADAIGAK SINCE 2002
全曲率の話
μ = |κ(s)| ds ≧2π 等号は卵形線のとき
≧4π 結び目があるとき
弧長ではないパラメータt で表したときは大きさ1 の単位ベクトルするための規格化が必要となります。
e'1(t) |p'(t)| = 0 κ(t) 0 e1(t) [Frenet-Serret の公式]
e'2(t) |p'(t)| -κ(t) 0 τ(t) e2(t)
e'3(t) p'(t) 0 -τ(t) 0 e3(t)