B02　剛体の回転運動
f-denshi.com  ［目次へ］最終更新日：10/01/30　　　　　たぶん，これでいいのでは，
サイト検索

１．角速度ベクトル

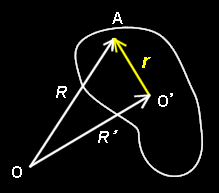［１］　原点をOとする静止座標系Σ：{ｅ1,ｅ2,ｅ3}と，剛体に固定されたまま，その１点(重心など) O' の周りを回転する動座標系，

Σ'：{ｅ'1(t),ｅ'2(t),ｅ'3(t)}　

を考えます。(以下，黄色で動座標系 であることを示してます。)このとき，時刻 t の関数である静止座標系の位置ベクトルR (t)は，

R (t)　＝R1ｅ1＋R2ｅ2＋R3ｅ3≡( R1(ｔ),R2(ｔ),R3(t))

または，         

R (t)　＝R ' ＋ r
        ＝R'1ｅ1＋R'2ｅ2＋R'3ｅ3 ＋ r1ｅ'1＋r2ｅ'2＋r3ｅ'3  

と書くことができます(右図参照)。ここで，静止座標の原点Oから動座標の原点O’を指すベクトルをR 'としています。

このベクトルを時刻 t で微分すると，

dR ＝ dR' ＋ dr1 ｅ'1＋ dr2 ｅ'2＋ dr3 ｅ'3＋r1 dｅ'1 ＋r2 dｅ'2 ＋r3 dｅ'3 　　･･･　(１)
dt dt dt dt dt dt dt dt

となります。動座標系の基底が時間の関数であることに注意してください。

［２］　さらに，動座標系Σ'の基底として正規直交座標を選んでいれば，

ｅ'j･ｅ'k＝δjk      (j，k＝1，2，3 )

も満足します。これを微分すると，

dｅ'j ｅ'k＋ｅ'j dｅ'k ＝0　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　･･･　(２)　　
dt dt

となります。また，Σ'の各基底ベクトルの時間微分もベクトルなのでΣ' の基底の１次結合で表せるはずです。それを，

dｅ'1 ＝a11ｅ'1＋a21ｅ'2＋a31ｅ'3
dt
dｅ'2 ＝a12ｅ'1＋a22ｅ'2＋a32ｅ'3
dt
dｅ'3 ＝a13ｅ'1＋a23ｅ'2＋a33ｅ'3
dt
   　　　　　　　　　　　　　　　　　　　　　　　　　　　 ･････　(３)

と書くことにします。これらを(２)式に

dｅ'j 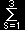＝ asjｅ's
dt
，
dｅ'ｋ 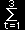＝ atkｅ'ｔ
dt

と表記して代入すれば，

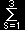asjｅ's ･ｅ'k＋ｅ'j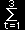･ atkｅ'ｔ
＝asjδsk＋atkδjt　
＝akj＋ajk　＝0

という関係が得られます。つまり，係数 ajk は交代行列[#]の成分なので，

ω1≡-a23 ＝a32，　ω2≡-a31＝a13，　ω3≡-a12＝a21，

とおくことができて，(３)式は形式的に，

dｅ'1
dt
＝ 0 ＋ω3ｅ'2−ω2ｅ'3 ＝ 0 ω3 −ω2 ｅ'1 　 　　　　　　　  ･･･　(３)'
dｅ'2
dt
−ω3ｅ'1＋0＋ω1ｅ'3 −ω3 0 ω1 ｅ'2
dｅ'3
dt
ω2ｅ'1−ω1ｅ'2＋0 ω2 −ω1 0 ｅ'3

と書き直すことができます。ここの右辺の交代行列が回転を意味していることはこのままではわかりにくいですが，ω1＝ω2＝0　とおいた，

dｅ'1 ＝ω3ｅ'2　
dt
dｅ'2 ＝−ω3ｅ'1
dt
dｅ'3 ＝　0
dt

とすれば，右図のようなｅ'3 の周りの回転を表していることはわかりますね。

［３］　より一般的には，角速度ベクトルと呼ばれる，(厳密には交代行列に対応する擬ベクトル)

ω＝ω1ｅ'1＋ω2ｅ'2＋ω3ｅ'3＝[ω1，ω2，ω3]　　　　　　　　　　　　　　　   ･････　(４)

を定義すると，(３)'式はベクトル積を用いて，

dｅ'j ＝ω×ｅ'j 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　･････　(３)”
dt

と書けます。例えば，

dｅ'1 ＝(ω1ｅ'1＋ω2ｅ'2＋ω3ｅ'3)×ｅ'1
dt
　　　　＝ω2ｅ'2×ｅ'1＋ω3ｅ'3×ｅ'1
　　　　＝−ω2ｅ'3＋ω3ｅ'2

など・・。つまり，ｅ'jの時間変化の方向はωとｅ'jの外積で表すことができ，この両方に垂直です。ベクトルωは動座標の回転軸方向を向いていることが確かめられます。これらを(１)に代入すると，

dR ＝ dR' ＋ dr1 ｅ'1＋ dr2 ｅ'2＋ dr3 ｅ'3 ＋ω×(r1ｅ'1＋r2ｅ'2＋r3ｅ'3)
dt dt dt dt dt
　　　　＝ dR' ＋ dr ＋ω×r　　　　　　　　　　　　　　　　　　　　　　　　　　　　　･･･　(１)'
dt dt
 　↓　動座標系Σ'の原点O’が静止座標系Σから見て静止していれば，dR' /dt = 0
dR ＝ dr ＋ω×r　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　･････　[*]
dt dt

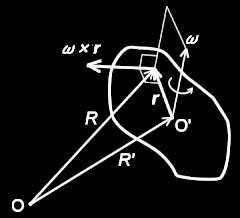
[*]は，静止座標系(原点O)からみた位置ベクトルの時間変化を，「剛体に固定された動座標系(原点O’)上の位置ベクトルの時間変化と動座標系の原点O’周りの回転ベクトルの合成」で表すための式です。ただし，２つの系の原点どおしは互いに相対運動はしていない，もしくは，そのような並進的な運動を無視するという条件が付いています。



２．慣性テンソル

［１］　さて，ベクトル R は剛体のある１点をさす位置ベクトルとします。すると，剛体に固定され，一緒に回転する動座標系Σ'（原点O’）で表わした剛体内の点を指す位置ベクトルr  は時間変化しない定ベクトルなので，[*]　において，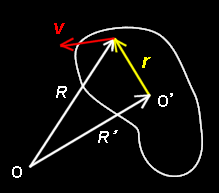

dr ＝0
dt

すなわち，静止系から見た剛体内の点 R の速度V は，

V ＝ dR  ＝ω×ｒ　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　･･･　(５)
dt

と，動座標系の角速度ベクトルと位置ベクトルで表すことができます。

［２］　力学において，点O’　に関する角運動量L は，剛体の密度分布をρ(r )とし，点R の速度V として(５)を用い，dr3＝dr1dr2dr3 として，

L　＝ ρ(r )r ×V dr3
   ＝ ρ(r )r ×(ω×r )dr3

と定義 [#]されます。ベクトル三重積の公式[#] を用い，さらに計算を進めると，

   ＝ ρ(r ){(r ･r )ω −(r ･ω )r }dr3
　　　　　　　　　　　↓　テンソル積で表現して　[#]
 　＝ ρ(r ){(r ･r )Eω−r 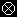r (ω)}dr3
　　≡　I (ω)  　　←　擬ベクトルです

ただし，I は慣性テンソルといい，「角速度ベクトルω を角運動量L に対応させる線形写像」 となっています。また，E は３次元単位テンソルで，テンソル積： (b ･x )a ＝a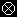b(x )[#]　なる記号も用いました。すなわち，｛　　｝の中の第１項は，

(r ･r )Eω＝(r12 ＋r22＋r32) 1　0　0 ω1
0　1　0 ω2
0　0　1 ω3

第２項は，

(r ･ω)r ＝ r1r1ω1＋r1r2ω2＋r1r3ω3
r2r1ω1＋r2r2ω2＋r2r3ω3
r3r1ω1＋r3r2ω2＋r3r3ω3
                ＝  r12  r1r2  r1r3 ω1
r1r2   r22  r2r3 ω2
r1r3  r2r3   r32 ω3

のように行列で書くことができます。したがって，角運動量を成分で書くと，

L　＝ L1 ＝ ρ(r ) r22＋r32 -r1r2 -r1r3 ω1 dr3  
L2 -r2r1 r32＋r12 -r2r3 ω2
L3 -r3r1 -r3r2 r12＋r22 ω3

まとめると，

［ L ＝ I(ω) の成分表示 ］
L1 ＝ I11 I12 I13　 ω1  ･･････　[**]
L2 I21 I22 I23 ω2
L3 I31 I32 I33 ω3
［慣性テンソル］
 　　　I　≡ ρ(r ){(r ･r )E −r r }dr3　　
　　　Ijk ≡ ρ(r ){( r12＋r22＋r32 )δjk−rjrk }dr3　　　
*　一般に角運動量ベクトルと角速度ベクトルは同じ方向を向いていません。

［３］　また，慣性テンソルの成分には名前がついていて，

  I11 ，I22 ，I33　 を慣性モーメント
−I12 ＝−I21
−I23 ＝−I23
−I31 ＝−I31		 を相乗モーメント(慣性乗積)

と呼びます。力学の教科書に合わせて，r1＝x，r2＝y，r3＝z　と書いて，Ijk を書き下ろせば，

Ixx ≡ ρ(r )(y2＋z2 )dr3
Iyy ≡ ρ(r )(z2＋x2 )dr3
Izz ≡ ρ(r )(x2＋y2 )dr3
Iyz ＝Izy≡− ρ(r )yzdr3
Izx ＝Ixz≡− ρ(r )zxdr3
Ixy ＝Iyx≡− ρ(r )xydr3

ただし，dr3 ＝ dxdydz。

３．オイラーの方程式　［固定点の周りの回転運動］

［１］　慣性テンソルは対称テンソルなので，直交行列を用いた基底変換によって対角化可能です[#]。剛体に結びついている動座標系Σ'＝{ｅ'1，ｅ'2，ｅ'3　}として，慣性テンソルが対角行列になるような正規直交基底を選んでおけば，[**]は，一般性を失うことなく，

L1 ＝ I1 0 0 ω1 ＝ I1ω1 ； I ≡ I1 0 0
L2 0 I2 0 ω2 I2ω2 0 I2 0
L3 0 0 I3 ω3 I3ω3 0 0 I3
⇔　　　 L ＝Iω＝I1ω1ｅ'1＋I2ω2ｅ'2＋I3ω3ｅ'3             　　　　　　　　　　　　　　　　         ･･･　(６)

と表されます。ここで用いられる基底：{ｅ'1，ｅ'2，ｅ'3}を慣性主軸，慣性テンソルの固有値を，I1，I2，I3 を主慣性モーメントといいます。この慣性主軸を求めるための基底変換は，剛体に固定されている基底どおしの間における基底の変換なので，剛体の運動状態とは関係なく剛体が与えられれば計算ができるということです。これは重要なことです。この慣性主軸を用いると，

 ω　 ＝ω1ｅ'1＋ω2ｅ'2＋ω3ｅ'3　　
 L　 ＝L1ｅ'1＋L2ｅ'2＋L3ｅ'3　

これを，[*]式の導出と同様に(６)の微分を考えて，　(L　＝Iω )

dL ＝I1 dω1 ｅ'1＋I2 dω2 ｅ'2＋I3 dω3 ｅ'3 ＋I1ω1 dｅ'1 ＋I2ω2 dｅ'2 ＋I3ω3 dｅ'3 　　･･･　(７)
dt dt dt dt dt dt dt

さらに(３)’，（３）”，（６）を用いて，　　　　　　　　　　　　　　　　　　                                    　

＝I1 dω1 ｅ'1＋I2 dω2 ｅ'2＋I3 dω3 ｅ'3 　＋ I1ω1(ω3ｅ'2−ω2ｅ'3)＋I2ω2(ω1ｅ'3−ω3ｅ'1)＋I3ω3(ω2ｅ'1−ω1ｅ'2)
dt dt dt
＝ I   dω ＋ω×Ｉω
dt

と書けます。力学によれば，これは力のモーメントN に等しく [#]，それを，

N  ＝N1ｅ'1＋N2ｅ'2＋N3ｅ'3　

とすると，オイラーの角運動方程式と呼ばれる回転の運動方程式が得られます。成分で表示すれば，

オイラーの角運動方程式
N1＝I1 dω1 −(I2−I3)ω2ω3　　　［ｅ'1 成分］
dt
N2＝I2 dω2 −(I3−I1)ω3ω1　　　［ｅ'2 成分］
dt
N3＝I3 dω3 −(I1−I2)ω1ω2　　　［ｅ'3 成分］
dt

念のために注意を喚起しておくと，角運動方程式は剛体に固定された座標系で表示されています。

４．固定軸の周りの回転運動

［１］　時間に依存しない定ベクトル(＝固定軸)n の周りの回転が，動座標系Σ' で，　

ω＝ωn＝ω(n1ｅ'1＋n2ｅ'2＋n3ｅ'3)；　｜n｜＝ 1
I(ω )＝ωI(n )         ( ←  I の線形性より )

であたえられるとします。ここで，　　

dI(ω )  ＝ dω  I　(n )
dt dt

すると，(７)式は次の様に書き換えられます。

dL ＝I(n ) dω ＋(ωn )×(ωI(n ) )
dt dt
          ＝ dω  I(n )＋ω2{n ×I(n)}
dt

これは原点 O’ の周りの力のモーメントN に等しくなければいけません[#]。今の場合，回転軸はn に固定されているので， n との内積をとり，n ･{n×I(n )} ＝ 0　であることに注意すれば，

dω n ･I(n)＝n ･N                    [ 回転運動方程式 １]
dt

成分で表すためには，

n ･I(n) ＝(n1，n2，n3) I11 I12 I13　 n1
I21 I22 I23 n2
I31 I32 I33 n3
＝ n12I11＋n22I22＋n32I33＋2n2n3I23＋2n3n1I31＋2n1n2I12

を注意すれば良いでしょう。さらに基底を慣性の主軸に選ぶと，

dω (n12I1＋n22I2＋n32I3)＝n ･N    [ 回転運動方程式 ２]
dt

特に回転軸が，n ＝(0，0，1)　と第３の主軸方向にあれば，

dω  I3＝N3                                 [ 回転運動方程式 ３]
dt

ともっとも簡単な場合の回転運動方程式になります。

------------------------------------------------------------------------

   ここで，回転軸と平行な角速度ベクトルωと角運動量ベクトルLとは一般的には同じ方向を向いていないということを注意しておきます。

例をあげておくと，質量の無視できる変形しない棒の両端に２つの重り (質量m) が結びつけられている剛体を考えます。下図。棒の中心O'には，30°で交わる回転軸が固定して取り付けられており，剛体はその回転軸の周りにのみ回転するとします。(回転軸も静止系に対して固定されているので，歳差運動するコマとは状況が違います。遊具の空中(回転)シーソーのようなものを思い浮かべるとよいでしょう。)

角速度ベクトルωの方向nは，静止系から見た場合でも，剛体に固定されている座標系から見た場合でも時間変化しません。(回転座標系では完全に静止して見える。) 動座標系の基底ベクトルは回転とともに方向を変えますが，角速度ベクトルの方向は回転によっても変化しないことをよく見て確認してください。

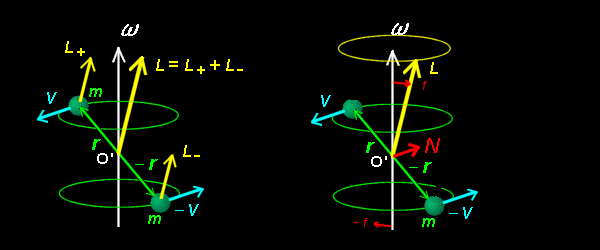
一方，角運動量は質量を結ぶ棒 (つまり，r ) に垂直であり，かつ，質量の速度ベクトルV に対しても垂直となっています。このとき，角運動量の方向は回転軸とは30°の角をなし，円錐を描くようにその周り回転しています。角運動量は時間変化しているのです。これは，角速度ベクトルが慣性の主軸方向と一致していないためです。この運動は「回転運動方程式１」，または ２で記述されます。この角運動量を回転させる力のモーメントは，遠心力によって，回転軸と棒とのなす角度が30°から90°へ広がろうとする力に抗するため，Ｏ’に働いている偶力 (上図のＮでLとは垂直〜Lは大きさ不変で方向だけを変える，Lの先端は回転軸の周りに周期ωで円運動。) によってもたらされます。(現実には回転軸の上下端にあるであろう軸受け部分から上記のような姿勢での回転を維持するための偶力Nが働いているため，静止系で系でLの先端は回転する。回転座標系では，この偶力と遠心力が釣り合っているので系は静止したままとなる。もちろん角運動量はゼロのまま。)

もし，回転軸が下図に示すように慣性の主軸に一致していれば，「回転運動方程式 ３」によってその運動は記述されます。この場合，等速回転において，角速度ベクトルの方向は不変です。


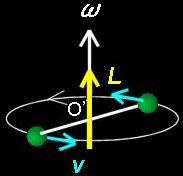
問題：回転軸と重りを固定する棒との角度が固定点O’において自由に変わるとき（回転シーソー），回転軸を回転させると重りはどのような運動をするでしょうか？

［目次へ］

補

質点系の(ニュ−トンの)運動方程式は，質点 j が質点 k から受ける力を　ｆjk とすれば，質点 j の運動方程式は，

d(mjvj)  ＝fj(外力)＋ fjk　　　　　　　　　　　　　　　　　　　　　　　　　　　　･････(1)
dt

この系の原点O' に関する角運動量は，各質点の位置ベクトル rj とのベクトル積を考えて，

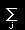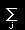rj × d(mjvj) ＝  (rj× fj) ＋ ( rj×fjk)　　　･････(2)
dt

右辺の第２項を，j＜k　のときと k＜ｊ のときに分けてかくと

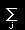(rj×fjk)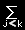＝ (rj×fjk)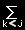＋ ( rj×fjk)
↓ 第２項のk と j の記号を交換
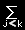                          ＝ (rj×fjk)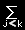＋ (rk×fkj)
↓fkj＝−fjk
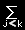                         ＝ (rj×fjｋ)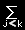＋ −(rk×fjk)
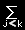                         ＝ (rj−rk)×fjk＝0

最後のところは，(rj− rk) と fjk は同じ直線上にある(作用反作用の法則)ので，そのベクトル積は 0 というわけです。

よって，(2)は，

d  {Σrj×(mjvj)}＝Σｒj× fj 
dt

となります。ここで，

L ≡Σrj×(mjvj)

を定義して，質点系の角運動量，また，

N ≡Σｒj×fj　

を定義して力のモーメントと呼ぶと，

dL  ＝N
dt

と書くことができます。質点が連続的にρ(r )で分布しているときは，

L　＝ ρ(r )r ×v (r) dV

を角運動量と定義できます。ただし，v (r)は位置r の物体の速度です。

［目次へ］