| Appendix 微分形式とは | |
| f-denshi.com [目次へ] 最終更新日: 15/10/31 簡略版 | |
| サイト検索 | |
体積,面積,長さを求める積分をパラメーター表示で表すと,
V= ∂r ・ ∂r × ∂r dudvdw= |J(xyz/uvw)|dudvdw ∂u ∂v ∂w
S= ∂r × ∂r dudv = |J(xy/uv)|dudv ∂u ∂v
r= ∂r du = |J(x/u)|du ∂u
となり,いずれもヤコビの行列式で示されます。このように書いてみると何か「背後に潜む共通性」が感じられますね。さらに本文中のベクトル解析の積分定理を並べて書いてみると,
divA dV = ∂V A ・dS (ガウスの定理)
rotA ・dS = ∂S A ・dr (ストークスの定理)
さらに,微分積分学の基本定理の3次元バージョンである線積分は,
grad f ・dr =|
∂C f (=[f] =f(b)−f(a) )
となります。ここで,f=f(x,y,z),Aの成分,Aj=Aj(x,y,z)はC∞級の関数とします。これらを眺めてみると,いろいろな次元の微分,積分や異なる次元にまたがる定理には次元に依存しない対称性,共通性がきっとあるに違いないと確信することになるのではないでしょうか。これから説明する微分形式とは,もともとは微分方程式論の中で芽生えた概念ですが,次元を超えた幾何学的特長や解析的な法則の簡明な記述に大変有用であることがわかり,その分野(微分幾何学,多様体)で発展してきた「基本ツール」ということができます。以下,その序論だけを手短に述べたいと思いますが,はじめにそのベースとなる外積代数についての話をしておかなければなりません。
[1] 各次元の微分量のパラメーター表示を思い出してみるとヤコビアン,すなわち,行列式が共通項として現れることに気がつきます。この行列式の代数的な性質を抽出した代数体系が外積代数ということができます。行列式の計算規則はこちらを参考にしてください。 ⇒[#]
外積代数は,ベクトル空間 の一種 (厳密にはベクトル空間Vの双対空間V*の直積集合![]() nV* (多重線形関数の集合) の中から交代性をもつものだけを選び出した集合 (部分空間)
で,ΛnV* と表記されるものです。) であって,ベクトルの間にウェッジ積と呼ばれる演算「∧」を定義し,ベクトルej 間でこの演算を繰り返すことで得られるすべての元,ei,ej∧ek,ei∧ej∧ek,・・・ などを基底とするベクトル空間です。ただし,ウェッジ積は次のような規則が課された演算です。
nV* (多重線形関数の集合) の中から交代性をもつものだけを選び出した集合 (部分空間)
で,ΛnV* と表記されるものです。) であって,ベクトルの間にウェッジ積と呼ばれる演算「∧」を定義し,ベクトルej 間でこの演算を繰り返すことで得られるすべての元,ei,ej∧ek,ei∧ej∧ek,・・・ などを基底とするベクトル空間です。ただし,ウェッジ積は次のような規則が課された演算です。
[ ウェッジ積の計算規則 ]
交代法則: ej∧ek= −ek∧ej ,これより,ej∧ej=0ただし,n変数ならば,j,k=1,2,・・・n です。
結合法則: (ei∧ej)∧ek=ei∧(ej∧ek)
分配法則: ei∧(ej+ek)=ei∧ej+ei∧ek
(ウェッジ積は外積とも呼ばれますが,初等的ベクトル解析の範囲で使われる外積(=ベクトル積)「×」と区別するため,ここではウェッジ積と呼ぶことにします。
このウェッジ積を用いると,n次正方行列 (線形作用素) A に対して,行列式は次式を満足する|A|として定義することができます。
Ae1Λ・・・・・ΛAen=|A| (e1Λ・・・・・Λen)
実際,n=2の場合に確かめておきましょう。aijを実数として,
Ae1=a11e1+a12e2
Ae2=a21e1+a22e2
を満足する線形作用素Aを考え,定義に基づいて計算すると,
Ae1ΛAe2=(a11e1+a12e2)Λ(a21e1+a22e2)
=(a11e1+a12e2)Λa21e1+(a11e1+a12e2)Λa22e2
=a11a21e1Λe1+a12a21e2Λe1+a11a22e1Λe2+a12a22e2Λe2
=(a11a22−a12a21)e1Λe2
すなわち,|A| =(a11a22−a12a21)となり,線形代数で習う行列式と同じであることを確認できます。
[2] 微分形式においては,ベクトルejの代わりに変数 (空間座標) の微分量dxjを考えます(無限小である必要はない)。きちんと書いておくと,
[ ウェッジ積の計算規則 ]
交代法則: dxj∧dxk = −dxk∧dxj ,これより,dxj∧dxj=0ただし,3変数の場合は,=1,2,3 を考える。
結合法則: (dxi∧dxj)∧dxk=dxi∧(dxj∧dxk)
分配法則: dxi∧(dxj+dxk)=dxi∧dxj+dxi∧dxk
厳密には dxj の基底をej として,dxj∧dxk ⇒ dxjej ∧dxkek のように表記すべきなのでしょうが,実際は上のように基底をej を省略して書きます。ベクトル場を考えるときは dxi そのものを(双対)基底とみなします。二次元ならば,dxj∧dxk が基底です。
3次元ユークリッド空間R3上で考える場合,この規則の下でウェッジ積を繰り返して得られる”基底”は,
dx,dy,dz,dy∧dz,dz∧dx,dx∧dy, dx∧dy∧dz
の7つで尽くされます。ウェッジ積を繰り返すことで,無限個の基底が作りだされない理由は,4つ以上の微分量dxjの積から作られる元は計算規則からすべて0となるからです。たとえば,
dx∧dy∧dzΛdx= −dx∧dyΛdx∧dz
= (dxΛdx)∧dy∧dz
=0∧dy∧dz=0
というようにです。
通常のベクトル空間においてベクトルに掛かるスカラー係数 (実数など) の代わりに,外積代数ではスカラー関数(実数関数)を対応させます。したがって,R3上の外積代数の任意の元はスカラー関数を,f0=f0(x,y,z),f1=f1(x,y,z),・・・として,
ω=f0+f1dx+f2dy+f3dz+f4dy∧dz+f5dz∧dx+f6dx∧dy+ f7dx∧dy∧dz
という式で表されることになります。つまり,この 「R3上の外積代数」 は,スカラー関数項の基底として1を先程の7つの基底に追加した8次元のベクトル空間です。(一般的には変数の数がnならば2n次元となる。)
[3] さて,もうひとつの元を,
γ=g0+g1dx+g2dy+g3dz+g4dy∧dz+g5dz∧dx+g6dx∧dy+ g7dx∧dy∧dz
とすると,先ほどの元との和は,ベクトルの和に倣って,
(f0+g0)+(f1+g1)dx+(f2+g2)dy+(f3+g3)dz
+(f4+g4)dy∧dz+(f5+g5)dz∧dx+(f6+g6)dx∧dy+(f7+g7)dx∧dy∧dz
と定義されます。さらに,2つのベクトルの間にウェッジ積を考えることができますが,4つの以上のdxiが掛け合わされると0となることに注意して計算すると,
ωΛγ=f0g0+(g0f1+f0g1)dx+・・・+(f1g2−g1f2)dx∧dy+・・・(・・・)dx∧dy∧dz
途中,・・・のところは省略しましたが,簡単に確認できますね。
[4] このベクトル空間から部分ベクトル空間を取り出して次のように分類し,その基底に含まれるdxiの数 p によって,p-形式と呼びます。
ωp∈Λp(R3) [R3上のp-形式 の集合]
具体的に書くと,
[ p-形式ωp ] 0-形式 (スカラー関数の集合 Λ0(R3)
ω0 = f1-形式 (基底,dx,dy,dz で張られる元の集合 Λ1(R3)
ω0(f) ≡ fω1 = A1dx+A2dy+A3dz2-形式 (基底,dy∧dz,dz∧dx,dx∧dy で張られる元の集合) Λ2(R3)
ω1(A) ≡ A ・drω2 = A1dy∧dz+A2dz∧dx+A3dx∧dy3-形式 (基底,dx∧dy∧dz で張られる元の集合) Λ3(R3)
ω2(A)≡ A ・dSω3 =f dx∧dy∧dz
ω3(f) ≡f dV
ここで,f=f(x,y,z),A1=A1(x,y,z),A2=A2(x,y,z),A3=A3(x,y,z)は実数関数で,A =(A1(x,y,z),A2(x,y,z),A3(x,y,z))。また,それぞれ2列目には,形式的に,
dr ≡(dx,dy,dz)
dS ≡(dy∧dz,dz∧dx,dx∧dy )
dV≡ dx∧dy∧dz
を考えて,内積,A ・dr,A ・dS ,fdV などによる表記を示しています。本文中の表記法と一致しているので,ここでも違和感なく”使える” と思います。
したがって,R3上の外積代数 (〜R3上の微分形式の全体集合) E(R3) は4つのベクトル空間の直和[#]となっており,次のように表します。
E(R3)=Λ0(R3)+Λ1(R3)+Λ2(R3)+Λ3(R3)
↑ +は通常は丸で囲んだ+記号で表記します。
[5] 各p-形式の間におけるウェッジ積は以下のように計算されます。
公式
(1) ω1(A)∧ω1(B) =ω2(A×B)
(2) ω1(A)∧ω2(B) =ω3(A ・B)
(3) ω1(A)∧ω1(B)∧ω1(C) =ω3([ABC])
(4) ωp∧ωq=(-1)pqωq∧ωp
ここで,A =(A1(x,y,z),A2(x,y,z),A3(x,y,z)),B =(B1(x,y,z),B2(x,y,z),B3(x,y,z)),C =(C1(x,y,z),C2(x,y,z),C3(x,y,z)),[ABC]=A ・(B×C) はスカラー3重積です。
証明
(1) (A1dx+A2dy+A3dz)Λ(B1dx+B2dy+B3dz)
=A1B2dxΛdy+A2B1dyΛdx+A2B3dyΛdz+A3B2dzΛdy+A3B1dzΛdx+A1B3dxΛdz
=(A2B3−A3B2)dyΛdz+(A3B1−A1B3)dzΛdx+(A1B2−A2B1)dxΛdy
=(A×B)・dS
=ω2(A×B)
(2) (A1dx+A2dy+A3dz)Λ(B1dy∧dz+B2dz∧dx+B3dx∧dy)
=A1B1dx∧dy∧dz+A2B2dyΛdz∧dx+A3B3dzΛdx∧dy
=(A1B1+A2B2+A3B3)dx∧dy∧dz
=ω3(A ・B)
(3) ω1(A)∧(ω1(B)∧ω1(C))=ω1(A)∧ω2(B×C)
=ω3(A ・(B×C))
(4) ⇒ pdf
[1] 微分形式に対する形式的な微分演算として「外微分」を定義して導入します。定義は,
p-形式の元から,p+1-形式への線形写像 d : Λp(Rn) → Λp+1(Rn)
を外微分とし,次の計算規則を満たすこととします。(スカラーから勾配ベクトルを得る算法の一般化)
外微分の計算規則
(2) d(ωp+ωq) = dωp+dωq [線形性]
(1) df= ∂f dx+ ∂f dy+ ∂f dz [実関数の全微分] ∂x ∂y ∂z
3変数(n=3)の場合の具体的な定義内容は,f=f(x,y,z),A =(A1(x,y,z),A2(x,y,z),A3(x,y,z))として,
外微分の定義
(1) dω0(f) =df
(2) dω1(A)=dA1∧dx+dA2∧dy+dA3∧dz
(3) dω2(A)=dA1∧dy∧dz+dA2∧dz∧dx+dA3∧dx∧dy
(4) dω3(f) =df∧dx∧dy∧dz (=0)
と定めることができます。3変数の場合に,もう少し計算を進めると次のようになります。
各-形式の外微分
dω0= ∂f dx+ ∂f dy+ ∂f dz ∂x ∂y ∂z
dω1= ∂A3 − ∂A2 dy∧dz+ ∂A1 − ∂A3 dz∧dx+ ∂A2 − ∂A1 dx∧dy ∂y ∂z ∂z ∂x ∂x ∂y dω3=0
dω2= dA1 + dA2 + dA3 dx∧dy∧dz dx dy dz ベクトル解析的な記号を用いて書くと,
と書くことができる。
dω0(f) =grad f ・dr =ω1(grad f)
dω1(A) =rotA・dS =ω2(rotA)
dω2(A) =divA dV =ω3(divA)
dω3(f) =0
つまり,外微分をとると,形式数がひとつ増加するだけでなく,grad,rot,div という微分演算子が現れるというところが注目点です。
「2」 上の導出です。
| dω0(f)=df= | ∂f | dx+ | ∂f | dy+ | ∂f | dz=gradf ・dr =ω1(gradf) |
| ∂x | ∂y | ∂z |
dω1(A)=dA1∧dx+dA2∧dy+dA3∧dz
| = | ∂A1 | dx+ | ∂A1 | dy+ | ∂A1 | dz | ∧dx+ | ∂A2 | dx+ | ∂A2 | dy+ | ∂A2 | dz | ∧dy | ||||
| ∂x | ∂y | ∂z | ∂x | ∂y | ∂z |
| + | ∂A3 | dx+ | ∂A3 | dy+ | ∂A3 | dz | ∧dz | ||
| ∂x | ∂y | ∂z |
| = | ∂A1 | dy∧dx+ | ∂A1 | dz∧dx | + | ∂A2 | dx∧dy+ | ∂A2 | dz∧dy | ||||
| ∂y | ∂z | ∂x | ∂z |
| + | ∂A3 | dx∧dz+ | ∂A3 | dy∧dz | ||
| ∂x | ∂y |
| = | ∂A3 | − | ∂A2 | dy∧dz+ | ∂A1 | − | ∂A3 | dz∧dx+ | ∂A2 | − | ∂A1 | dx∧dy | ||||||
| ∂y | ∂z | ∂z | ∂x | ∂x | ∂y |
=rotA・dS =ω2(rotA)
dω2(A)=dA1∧dy∧dz+dA2∧dz∧dx+dA3∧dx∧dy
| = | ∂A1 | dx+ | ∂A1 | dy+ | ∂A1 | dz | ∧dy∧dz+ | ∂A2 | dx+ | ∂A2 | dy+ | ∂A2 | dz | ∧dz∧dx | ||||
| ∂x | ∂y | ∂z | ∂x | ∂y | ∂z |
| + | ∂A3 | dx+ | ∂A3 | dy+ | ∂A3 | dz | ∧dx∧dy | ||
| ∂x | ∂y | ∂z |
| = | ∂A1 | dx∧dy∧dz+ | ∂A2 | dy∧dz∧dx+ | ∂A3 | dz∧dx∧dy | ||||||
| ∂x | ∂y | ∂z |
| = | dA1 | + | dA2 | + | dA3 | dx∧dy∧dz | ||
| dx | dy | dz |
=divA dV =ω3(divA)
| dω3(f)=df∧dx∧dy∧dz= | ∂f | dx+ | ∂f | dy+ | ∂f | dz | ∧dx∧dy∧dz =0 | ||
| ∂x | ∂y | ∂z |
以上の定義の下で次の定理が成り立ちます。
定理
(1) d(ωp∧ωq) = dωp∧ωq+(-1)pωp∧dωq [ ライプニッツの法則 ]
(2) d(dωp)=0 ⇔ ベクトル解析の公式: rot grad f=0, div rotA=0 に相当
[3] 定理の(2) の3変数の場合の証明
d(dω0(f)) =d(ω1(gradf))=ω2(rot gradf)=ω2(0)=0
d(dω1(A)) =d(ω2(rot A))=ω3(div rot A)=ω3(0)=0
この意味は滑らかな関数の2階偏導関数が微分の順序によらず等しいことに対応しています。
[1] 微分形式の積分を定義し,本文中の様々な積分定理が,「一般次元のストークスの定理」ひとつにまとめられることを見ていきます。まず,その準備として引き戻しと呼ばれる写像について説明します。任意のp-形式について考えることができますが,0形式についての引き戻しを具体的に見てみるのがよいでしょう。
f(x,y,z) を X (=R3) 上の関数,
とし,C∞級のUからXへの1対1連続写像 Φ: t → (x,y,z) を,
Φ: x=x(t) ただし, t∈U, (x,y,z)∈X y=y(t) z=z(t)
とします。この状況の意味は3次元空間の曲線はひとつのパラメーターで表すことができるというものです。このとき,引き戻しΦ*とは,次のような合成写像から作られる線形写像です。
線形写像,Φ*f≡f○ Φ
すなわち,
Φ* : f(x,y,z) → f(t)=f(x(t),y(t),z(t)) または,Φ*f =f(x(t),y(t),z(t))
ということで,見かけは単にx,y,zにx(t),y(t),z(t)を代入しただけとなっています。これは,Xで定義されている関数をU上で定義しなおしたことに相当し,次のようにまとめることができます。
ところで,Uは必ずしもR1上にある必要はなく,R2,R3でも構いません。特にU=R3上への引き戻し,
Φ*f=f(x(u,v,w),y(u,v,w),z(u,v,w))
は3次元(ユークリッッド)空間上での通常の座標変換と同じことです。
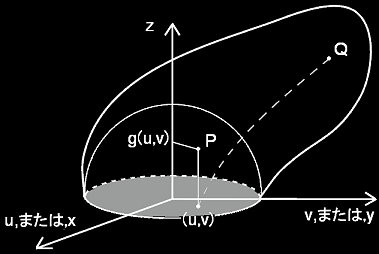
[2] R2上への引き戻しの具体例をあげておきます。半径1の半球面,X={ (x,y,z) | x2+y2+z2=1,z≧0 } の上で定義された関数f(x,y,z)を考えるとき,U={ (u,v)|u2+v2≦1} からXへの写像,
Φ: x=u,y=v,z=g(u,v)≡(1−u2−v2)1/2,
はC∞級の写像です。これは球面上の1点Pとuv平面上の1点(u,v)とが対応している1対1写像です。このとき,f(x,y,z) のu-v平面への引き戻しは,
Φ*f=f(u,v,g(u,v))
となります。これは+z方向から光を当てて,球面をxy平面へ投影したような写像となっている特殊なケースです。しかし,一般的には,uv平面上の円板をゴムを膨らますように連続的,立体的に引き伸ばしたり,縮めたりして変形させた3次元曲面を考えても,そこにはuv平面との間に1対1写像Φが定義できます。したがって,R2上への引き戻しとは,2次元平面への単純な射影と比べてはるかに自由度の大きい概念であることに注意しましょう。
[3] 以上は0形式に基づいた説明ですが,引き戻しは任意のp-形式に拡張して考えることができます。あるXとその上で定義された微分形式が与えられたとき,C∞級のΦ:U→Xに対して,引き戻しの線形写像Φ*に次のような要請を課すこととします。
p-形式に対して,
ωp∈Λp(X) とするとき,Φ*ωp∈Λp(U) Φ*ω⇒Φ*(ω)とも書く
すなわち,Φ*とはX上で定義された,p-形式をU上のp-形式に見直すことであり,さらに,
引き戻しΦ*に要請される性質
外積に対する線形性
(1) Φ*(ωΛω’)=Φ*(ω)ΛΦ*(ω’)外微分に対する可換性
(2) Φ*(dω)=dΦ*(ω)特に,Φ*(df)=d(Φ*f))=df(x(t),y(t),z(t))
を要求します。これらの性質は証明することもできます [#] が,ここでは上記の性質(1),(2)を引き戻しが満足すべき条件として話を進めます。このようにΦ*を規定すると,「C∞級の写像Φが与えられたとき,引き戻しは一意的に定まる。(定理)」ことを示すことができます。
[4] この要請に基づき,1次,2次の微分形式について具体的な計算を示すと次のとおりとなります。
1-形式の場合,
Φ=r(t)=(x(t),y(t),z(t)),
ω1(A)=A1(x,y,z)dx+A2(x,y,z)dy+A3(x,y,z)dz
に対して,
Φ*ω1=Φ*(A1(x,y,z))Φ*(dx)+Φ*(A2(x,y,z))Φ*(dy)+Φ*(A3(x,y,z))Φ*(dz)
=Φ*(A1(x,y,z))dΦ*(x)+Φ*(A2(x,y,z))dΦ*(y)+Φ*(A3(x,y,z))dΦ*(z)
=A1(r(t))dx(t)+A2(r(t))dy(t)+A3(r(t))dz(t)
=A1(r(t)) dx dt+A2(r(t)) dy dt+A3(r(t)) dz dt dt dt dt
=A(r(t))・ dr dt dt
2-形式の場合,
Φ=r(u,v)=(x(u,v),y(u,v),z(u,v)),
ω2(A)=A1(x,y,z)dy∧dz+A2(x,y,z)dz∧dx+A3(x,y,z)dx∧dy
に対して,
Φ*ω2(A)=Φ*(A1(x,y,z))Φ*(dy∧dz)+Φ*(A2(x,y,z))Φ*(dz∧dx)
+Φ*(A3(x,y,z))Φ*(dx∧dy)
=A1(r(u,v)) (dy(u,v)∧dz(u,v))+A2(r(u,v)) ((dz(u,v)∧dx(u,v))
+A3(u,v)) ((dx(u,v)∧dy(u,v))
=A1(r(u,v)) ∂y du+ ∂y dv ∧ ∂z du+ ∂z dv +・・・+・・ ∂u ∂v ∂u ∂v
=A1(r(u,v)) ∂y ∂z − ∂z ∂y du∧dv ∂u ∂v ∂u ∂v
+A2(r(u,v)) ∂z ∂x − ∂x ∂z du∧dv ∂u ∂v ∂u ∂v
+A3(r(u,v)) ∂x ∂y − ∂y ∂x du∧dv ∂u ∂v ∂u ∂v
=A(r(u,v))・ ∂r × ∂r du∧dv ∂u ∂v
以上が2-形式の引き戻しです。これは,パラメーター表示での面積分
A(u,v)・(ru×rv)dudv
の中身の部分に対応しています。
なお,3-形式の引き戻しは,R3への引き戻しとなりこれは通常の変数変換と同じになります。結果だけ書くと,
Φ*ω3(f)= f(r(u,v,w)) ∂r ・ ∂r × ∂r du∧dv∧dw ∂u ∂v ∂w
途中の計算は演習です。以上,はじめに提起した「背後に潜む共通性」への回答が含まれています。
[5] 最後に,ベクトル解析において説明した線積分,面積分,体積分と合理性をもった同一視によって,微分形式の積分の定義を与えます。
微分形式の積分の定義
ω=hdx1∧dx2∧・・・∧dxn に対して,
とする。

ω≡ ・・
hdx1dx2・・・dxn 1-形式 曲線C上の積分
ω1(A)≡ (A1dx+A2dy+A3dz)= A・dr 2-形式 曲面S上の積分
S ω2(A)≡ (A1dydz+A2dzdx+A3dxdy)= A・dS 3-形式 体積V上の
V ω3(f) ≡ f dxdydz
なお,0-形式の∂C(2点a,bにおける)積分は,
ω0(f)≡[f(r)] =f(b)−f(a)
と定義しておくとよいでしょう。
先程求めたように,1-形式の引き戻しは,
Φ*ω1(A)=A(r(t))・ dr dt = A(r)・dr =ω1(A) dt
両辺 (左はR1上tの関数,右はR3上(x,y,z)の関数) について,それぞれの対応する領域で積分して,
Φ*ω1(A)= ω1(A)
これは2-,3-形式も同様な表記となり,
∂D Φ*ω= D ω
と一般化されます。ここで,∂Dとは領域Dの周辺部(方向付)という意味です。
[6] 一般次元のストークスの定理
一般次元のストークスの定理
領域D上のn変数のp-形式について,次の等式が成り立つ。
∂D ω = D dω
一般論の厳密な証明 (⇒多様体入門 [#] ) はやめて,具体的に確かめてみます。
0-形式のストークスの定理 =3次元の微分積分学の基本公式 (線積分とポテンシャル)
左辺= ∂C ω0(f)= f(r)=f(b)−f(a)
右辺= C dω0(f)= C ω1(gradf)
= C gradf ・dr
∴f(r(a))−f(r(b))= C gradf ・dr
1-形式のストークスの定理 =いわゆるストークスの定理
左辺= ∂S ω1 (A)= C A・dr
右辺= S dω1 (A)= s ω2(rotA)= rotA・dS
∴ A・dr = rotA・dS
2-形式のストークスの定理 =いわゆるガウスの定理
左辺= ∂V ω2 (A)= A ・dS
右辺= V dω2 (A)= V ω3 (divA)= divA dV
∴ A ・dS = divA dV
| p | 0 | 1 | 2 | 3 | ||||||||||||||||||||||||||||||||||
| p-形式 ω |
f | A1dx+A2dy+A3dz A ・dr |
A1dy∧dz+A2dz∧dx+A3dx∧dy A ・dS |
f dx∧dy∧dz f dV |
||||||||||||||||||||||||||||||||||
| 微分 dω |
grad f ・dr | rotA・dS | divA dV | 0 | ||||||||||||||||||||||||||||||||||
| 引き戻し Φ*ω |
- |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||
| 積分定理 |
|
|
|
- | ||||||||||||||||||||||||||||||||||
⇒ pdf
注)ストークスの定理の証明
引き戻しΦ*: 任意の領域D ⇒ 領域A(u,v):[0,1]×[0,1] を介して,
D dω = A Φ*dω
= A dΦ*(ω)
= ∂A Φ*(ω)
= ∂D ω
を順に証明します。
参考書: 裳華房「曲線と曲面の微分幾何」小林昭七著 第4章1節(p.122-127)など