 |
12 t分布とF分布 |
| f-denshi.com 最終更新日:11/10/8 現状,個人的なメモ程度なのでそのうち噛み砕いて書き直すつもり |
| サイト検索 |
1.t分布の導出
[1] 確率変数 X1,・・・,Xn が独立に正規分布N(μ,σ)に従うとき,標本平均,
は正規分布N(μ,σ2/n)に従い,変数変換によって,
| Y~= |
X~−μ |
・・・・[*] |
|
|
|
|
| σ/ |
 |
n |
|
は標準正規分布N(0,1)に従うことはすでに述べた[#]。
[2] 一方,標本平均と不偏分散,
| X~= |
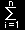 |
Xi |
|
| n |
| s2= |
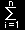 |
(Xi−X~)2 |
|
| n−1 |
は互いに独立であり, 統計量 (n-1)s2/σ2 を考えると,これは自由度(n−1)のカイ二乗分布に従うのであった[#]。すなわち,
である。
[3] 標本統計分析の分野では,Y~ が標準正規分布に従うことを利用して,母平均値μの推定を行うことが可能である[#]。しかし,実際の問題では[*]の分母にある母分散σの値も不明である場合が一般的である。そのような場合は標準正規分布を用いた推定を行うことはできない。その代わり,次のようにσを標本から計算可能な不偏分散sで代用することが行われる。
| X~−μ |
⇒ |
X~−μ |
= |
| X~−μ |
|
|
|
|
| σ/ |
 |
n |
|
|
= |
Y~ |
←N(0,1)に従う |
|
|
|
|
|
|
|
|
| σ/ |
 |
n |
|
|
|
|
| s/ |
 |
n |
|
|
|
←中身はχ2(n-1)/(n−1)に従う |
この右辺の確率変数に従う分布を(ステューデントの) t分布と呼ぶ。この確率変数の分子はN(0,1),分母は自由度(n-1)のカイ二乗分布をn-1で除したものであり,t分布は一意的に定まることがわかる。
記号をn-1→nと改めて定義をもう一度書くと,
|
定義
標準正規分布N(0,1)に従う確率変数Yと自由度nのカイ二乗分布に従う確率変数Zから作られる確率変数Tを
| T= |
Y |
|
|
|
 |
Z/n |
|
で定義する。ここで,YとZは互いに独立で,この確率変数Tの従う分布をt分布と呼ぶ。 |
この用語を用いれば,
| 統計量 |
X~−μ0 |
は自由度n-1のt分布に従う |
|
| s/√n |
|
と述べることができる。
[3] 次にこのt-分布の確率密度関数を標準正規分布,カイ二乗分布の確率密度関数と関連付けよう。
そのためには,2重積分の変数変換(y,z)→(t,u) として[#],
| y=t |
|
|
 |
u/n |
|
, z=u ・・・・[**] |
を考えれば良い。変換前の確率変数T,すなわち,Y/(Z/n)1/2 の従う確率密度関数をfYZ(y,z));-∞≦y≦∞,0≦z≦∞,変換後の確率密度関数を fTU(u,t);-∞≦t≦∞,0≦u≦∞,とすると,各確率密度関数を対応する積分範囲で積分すると,それらは相等しい確率を与えなければならない。すなわち,
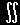 |
fYZ(y,z)dydz= |
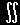 |
fTU(t,u)dtdu |
| = |
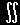 |
fYZ(y(t,u),z(t,u))|J(y,z/t,u)|dtdu |
を満足する。ここで,t分布を考えるときに,確率変数Uについては制限がないので,uの全範囲についてfTU(t,u)を積分してTの周辺確率密度関数,
| fT(t)= |
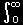 |
fTU(t,u)du |
|
|
を計算すれば,これが確率変数Tの従う確率密度関数となる。
[4] そこで,ヤコビアンを計算すると,
| |J(y,z/t,u)|= |
|
|
|
|
|
|
= |
|
|
|
|
 |
u/n |
|
|
|
|
|
| t |
 |
nu |
|
|
| 2 |
|
|
|
= |
|
|
 |
u/n |
|
|
|
|
0 |
|
1 |
また,確率変数YとZが独立であることから,
fYZ(y(t,u)z(t,u))=fY(y(u,t))・fZ(z(u,t))
との計算が許される[#]。ただし,fY(y),fZ(z)はそれぞれ標準正規分布とカイ二乗分布[#]の確率密度関数,
| fZ(z)= |
1 |
zn/2-1e−z/2 |
|
| 2n/2Γ(n/2) |
である。[**]をこれに代入して,
fTU(t,u)=fYZ(y(t,u),z(t,u))|J(y,z/t,u)|
| = |
1 |
・ un/2-1e-(t2/n+1)u/2 |
|
|
 |
u |
|
|
|
|
|
|
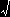 |
2π |
2n/2Γ(n/2) |
|
|
|
 |
n |
|
を得る。
[5] 次に周辺分布を求めるためにuについて,0≦u≦∞の範囲で積分を行うが,その際,変数の置き換え,
(t2/n+1)u/2=w と (t2/n+1)du=2dw を利用する。すなわち,
| un/2-1 |
|
|
 |
u |
|
du = |
 |
2w |
 |
(n-1)/2 |
2 |
dw |
|
|
| (t2/n+1) |
t2/n+1 |
| =2(n+1)/2・ |
w(n+1)/2−1 |
dw |
|
| (t2/n+1)(n+1)/2 |
であることに注意して計算する。すなわち,fT(t)≡f(t) は,
| f(t)= |
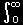 |
fTU(t,u)du |
| = |
2(n+1)/2 |
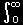 |
w(n+1)/2−1e-wdw |
|
|
|
|
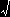 |
2πn |
2n/2Γ(n/2)(t2/n+1)(n+1)/2 |
|
| = |
1 |
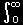 |
w(n+1)/2−1e-wdw |
|
|
|
|
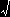 |
nπ |
Γ(n/2)(t2/n+1)(n+1)/2 |
|
| = |
1 |
・Γ((n+1)/2) |
|
|
|
|
 |
nπ |
Γ(n/2)(t2/n+1)(n+1)/2 |
|
で与えられる。最後のところでガンマ関数の定義[#]を用いた。さらに,ベータ関数,
| B(p,q)= |
Γ(p)Γ(q) |
[ベータ関数] |
|
| Γ((p+q) |
|
|
|
| Γ(1/2)= |
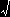 |
π |
を用いると,
とまとめることができる。
[6]
t分布の確率密度関数と標準正規分布N(0,1)との比較 ↓
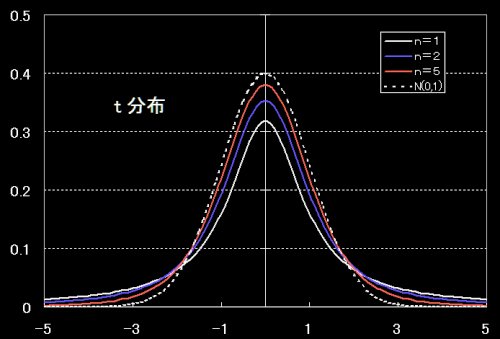
自由度1のとき,コーシー分布という。t分布は,n→∞でN(1,0)に一致する。
2. F-分布の導出
[1] 確率変数 Z1,Z2 がそれぞれ自由度n1,n2のカイ二乗分布に従うとき,確率変数,
の従う分布を自由度(n1,n2)のF分布という。これは,
の関係を思い出せば,2つの標本値から推定される分散(または標準偏差)どおしの比較に有用となることがわかるであろう。詳しいことは「第2部:統計分析」で説明する。ここでは具体的な分布関数の導出だけ行う。
[2] t分布で行ったように確率変数の変換,(Z1,Z2)→(Z,Y)を考える。ここで,確率変数Z1,Z2の従う確率密度分布を
f1(z1),f2(z2), 0≦z1≦∞,0≦z2≦∞
とする。Yの従う確率密度関数を
f12(z1,z2)
として,確率密度関数の積分変数の変換 (z1,z2)→(z,y),
z1=yz/n2
z2=z/n1 ←後々の都合を考えてこのようにおく。
を考える。t分布の導出と同様に考えて,変数変換後の確率密度関数をfZY(z,y)とすると,
 |
f12(z1,z2)dz1dz2= |
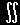 |
fZY(z,y)dzdy |
| = |
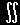 |
f12(z1(z,y),z2(z,y))|J(z1,z2/z,y)|dzdy |
ヤコビアンを計算すると,
| |J((z1,z2/z,y)|= |
|
|
|
|
|
|
= |
|
|
y/n2 |
z/n2 |
|
|
= |
|
|
|
|
1/n1 |
0 |
[3] したがって,Z1とZ2が独立な確率変数であることに注意して,
fZY(z,y)=f1(z1(z,y))・f2(z2(z,y))・|J|
| = |
1 |
z1n1/2-1e−z1/2 × |
1 |
z2n2/2-1e−z2/2 × |
z |
|
|
|
| 2n1/2Γ(n1/2) |
2n2/2Γ(n2/2) |
n1n2 |
| = |
yn1/2-1 |
・ z(n1+n2)/2-1e−(1/n1+y/n2)z/2 |
|
| 2(n1+n2)/2 n1n2/2 n2n1/2 Γ(n1/2)Γ(n2/2) |
周辺分布関数として,
| f(y)= |
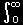 |
fZY(z,y)dz |
|
|
| = |
yn1/2-1 |
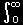 |
z(n1+n2)/2-1e−(1/n1+y/n2)z/2dz |
|
| 2(n1+n2)/2 n1n2/2 n2n1/2 Γ(n1/2)Γ(n2/2) |
↓ (1/n1+y/n2)z/2=w と積分変数を置き換えて,
| = |
yn1/2-1 |
・ |
2(n1+n2)/2 |
・ |
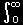 |
w(n1+n2)/2-1e−wdw |
|
|
| 2(n1+n2)/2 n1n2/2 n2n1/2 Γ(n1/2)Γ(n2/2) |
(1/n1+y/n2)(n1+n2)/2 |
| = |
n1n1/2 n2n2/2 |
・ |
yn1/2-1 |
Γ((n1+n2)/2) |
|
|
| Γ(n1/2)Γ(n2/2) |
(n2+yn1)(n1+n2)/2 |
変数記号y→xと代えて,
|
F分布の確率密度関数
| f(x)= |
n1n1/2 n2n2/2Γ((n1+n2)/2) |
・ |
xn1/2-1 |
|
|
| Γ(n1/2)Γ(n2/2) |
(xn1+n2)(n1+n2)/2 |
| = |
n1n1/2 n2n2/2 |
・ |
x(n1-2)/2 |
|
|
| B(n1/2,n2/2) |
(n1x+n2)(n1+n2)/2 |
|
F分布はフィッシャー(Fisher)分布とも呼ばれる。
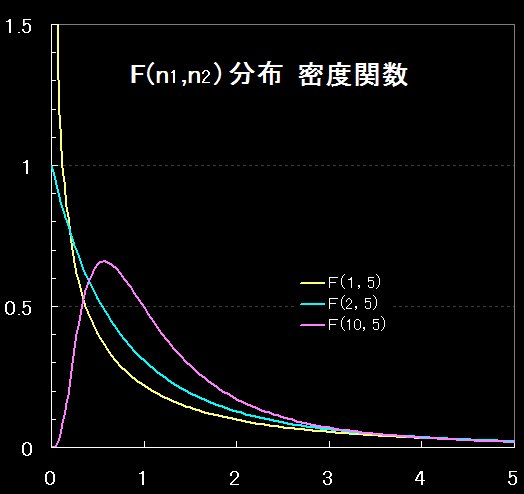
F分布の確率密度関数
[目次]

