| 10 ルベーグの収束定理 | ||
| f-denshi.com [目次へ] 最終更新日:11/9/23 (エゴロフの定理の間違い訂正) | ||
| サイト検索 | ||
積分の収束にまつわる重要な定理について考え方だけを示しました。教科書で勉強する前や行き詰まったときに目を通しておくと,大局的な理解の役に立つと思います。
[1]
|
エゴロフの定理: 有界な 測度空間 (X,β,m)上で定義された可測関数列が関数 f に収束している: すなわち, f1,f2,・・・,fn,・・・ → f のとき,任意の正数εに対して可測集合 H ( ⊂X ) が存在して, (1) m(H ) < εとできる。 |
証明は ⇒ [#]
要するに,定義域から「測度が零であるいくらでも小さな集合」 を適切に除外して考えれば,fn を f に一様収束するようにできるということです。
(上記の「零である」は間違いで,「いくらでも小さな」が正しい。指摘してくれたTKさんありがとうございました。)
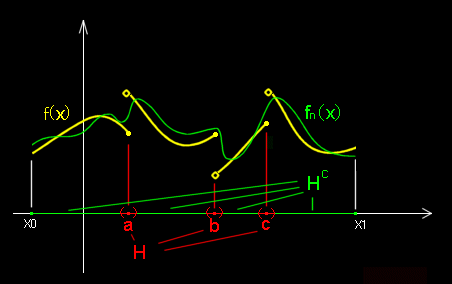
[2] 例えば,右に示すような a,b,c で不連続点をもつ不連続関数 f(x) に対して一様収束するような,[x0,x1]で連続な関数列 fn(x) は存在しません。
ところが,この不連続点を含むε-近傍の和集合
H=Vε1(a)∪Vε2(b)∪Vε3(c)
を取り除いた部分 Hc で考えると,一様収束する fn(x) が存在して,
ε1+ε2+ε3
はいくらでも小さくとれ,m(H) <ε とできる ということをいっているのです。
この定理によって,可測関数を一様収束する部分と一様収束しないいくらでも小さいな部分と分離できることが分かります。
[1]
|
積分の基本定理 f(x) を測度空間 (X,β,m)上で定義された可測関数で,単調増加する単関数の列: 0 ≦η1(x)≦η2(x)≦ ・・・・ を用いて,
と表せるとき,E∈β 上の積分において,
である。 つまり, 極限と積分の順序が交換可能 |
エゴロフの定理を単関数に適応することで,可測関数に収束する単関数の列の積分と極限操作は交換できることが分かります。
この事実のために,ルベーグ積分における積分と極限の順番が交換可能である条件から,リーマン積分のときは必要だった「一様収束」という文言が「単関数を介したルベーグ積分の定義」の中に隠されて見えなくなっているのです。
[2] さらに積分の基本定理を利用して,一般の可測関数の単調増加列,
0 ≦g1(x)≦g2(x)≦ ・・・・
が,g(x) に収束するとき,
g(x)m(dx)= gk(x)m(dx)= gk(x)m(dx)
であることも証明できます(単調収束定理)。(2023/3/1 挿入)
[3] そして,これを用いて,単純増加列とは限らない非負値関数の列 {fn} に対して,ファトゥーの不等式が導かれます。
|
ファトゥの不等式 非負な値をとる可測関数の列{fn(x)}について,が成り立つ。 (2015/7/6 挿入) |
|||||||||||
これは,gk(x)=inf { fk(x),fk+1(x),・・・ } とおくと,
gk(x)≦fk(x)
liminf k→∞ fk(x)= gk(x)
および,
0≦g1(x)≦・・・≦gk(x)≦gk+1(x)≦ ・・・
なので,gkに単調収束定理を適用できて,
liminf k→∞ fk(x)m(dx)= gk(x)m(dx)
= gk(x)m(dx)=
liminf k→∞ gk(x)m(dx) ≦
liminf k→∞ fk(x)m(dx)
が成り立つからです。
[4] さらに,この不等式で等号が成立する場合の条件を提示した定理がルベーグの収束定理です。
| ルベーグの収束定理 [ 項別積分可能条件 ] f(x)に収束する(各点収束でよい)可測関数列: f1(x),f2(x),・・・・ について,適当な可積分関数 F(x) が存在して, |fk(x)|≦F(x) , k=1,2,3,・・・ が成り立つならば,任意の可測集合E上で,
がなりたつ。 ここで,F(x)を優圧関数という。 |
この定理の証明には, F(x)±fk(x) ≧ 0 に注意して,ファトゥーの不等式を用います。
証明は ⇒ [#]
[5] リーマン積分において,この定理に対応する次の定理を書いておきましょう。
|
ルベーグの収束定理の リーマン積分バージョン 区間 [a,b] 上の連続関数 f(x) に収束する連続関数列 f1(x),f2(x),・・・・ について, |fk(x)|≦K , k=1,2,3,・・・ が成り立つならば,
がなりたつ。 |
この定理の意味は,
⇒ 一様収束すれば,極限と積分の順序が交換できる。 ⇒ 証明 [#]
なおここで,K は優圧定数などとはいいませんが,先の優越関数に対応していることはわかりますね。
ルベーグ積分の計算では,エゴロフの定理から可測関数については一様収束するものとして扱ってよいので,「一様収束」という条件は不要となっているのです。
(1) x∈X, lim fj(x) =f(x) のとき
An(k)≡{ x|j ≧n のとき|fj(x)−f(x)|<(1/2)k }
を定義すると,
An(k)∈β
fj(x)−f(x)は可測関数
であり,
A1(k)⊂A2(k)⊂・・・An(k)⊂・・・⊂A∞(k)=X
なので,ある p が存在して,
m(X)−m(Ap(k)) < (1/2)k
とできる。
すると,任意の実数εに対して,
ε>(1/2)q
となる q を選んで,可測集合,
H=
∞ U k=q+1 Ap(k)c
を考えると,
m(H) ≦
∞ Σ k=q+1 m( Ap(k)c )
=
∞ Σ k=q+1 (m(X)−m(Ap(k))) <
∞ Σ k=q+1 (1/2)k
=(1/2)q <ε
である。
(2) lim fj(x) =f(x) がHcで一様収束していることは,
任意の正数δに対して,
(1/2)k <δ,かつ,(1)における p と q に対応して,k>q+1となる
十分大きな k ( =十分小さな(1/2)k ) を考えると,x∈Hc ならば,
x∈Ap(k) であり,j ≧p のとき|fj(x)−f(x)|<(1/2)k <δ
となっていることから分かる。
ルベーグの収束定理の証明 ( F(x) を F,fk(x) を fk と略記する。)
F(x)+fk(x) ≧ 0 をファトゥーの不等式に代入して,
liminf k→∞ (F+fk) m(dx)≦
liminf k→∞ (F+fk) m(dx)
⇔ (Fの積分はキャンセル)
liminf k→∞ fk m(dx) ≦
liminf k→∞ fkm(dx) ・・・ (11)
F(x)−fk(x) をファトゥーの不等式に代入して,
liminf k→∞ (F−fk) m(dx)≦
liminf k→∞ (F−fk) m(dx)
⇔ (Fの積分はキャンセル)
liminf k→∞ (−fk )m(dx) ≦
liminf k→∞ (−fk)m(dx)
さらに,一般的に実数列に対して,
liminf k→∞ (−ak)=−
limsup k→∞ ak
であることに注意すれば,
−
limsup k→∞ fk m(dx) ≦−
limsup k→∞ fkm(dx) ・・・ (12)
と書き換えられる。
(11)と(12)を用いると,
|
fk | m(dx) ≦ |
|
fkm(dx) ≦ |
|
fkm(dx) ≦ |
|
fk | m(dx) |
ここで,仮定より { fk(x) } はf(x)に収束するので,この式の両端は等しく,
f(x) m(dx)
と表される。このとき,中央の不等式も等号が成り立ち,これは,
fkm(dx)
と書いてよい。すなわち,
f(x) m(dx) = fk(x)m(dx)
が成り立っている。