|
Appendix 3 ∫と |
|
| f-denshi.com [目次へ]最終更新日: 21/09/08 | ||
| サイト検索 | ||
本文中では省略した「極限の交換」[#] の正当性を証明しましょう。
(販売していたPDFからの抜粋です。)
[1] 有限項の連続関数列の和に対して,
(f1(z) +・・・ + fn(z) ) dz = f1(z) dz +・・・ + fn(z) dz
が成り立ちますが,これは,
fk(z) dz = fk(z) dz
と書直してみれば,![]() と
と ![]() とが交換可能であることを示しています。問題は,n →∞ のときは
とが交換可能であることを示しています。問題は,n →∞ のときは
どうなるのかですが,その答えは次の定理として与えられます。
|
【定理1】 一様収束する関数列に関する極限の交換 曲線C 上で連続関数の列 fn(z) が一様収束 [#] すれば,その極限関数 f (z) に対して,
が成り立つ。 |
[2] [証明]
( ステップ1 )
関数列 fn(z) の極限 f (z) は連続関数であることを示す。
C 上での fn(z) の一様収束性より,任意のεに対して,ある N が存在して,n>N を満たすn を選ぶと,C 上のすべての z に対して,
|f (z)−fn(z)|<ε/3 (当然, z’∈C , z’≠ z に対しても成り立つ。)
とすることができます ( 一様収束の定義そのまま) 。一方, fn(z) は連続関数なので,同じε/3 に
対して,あるδ が存在して,
|z'−z|<δ,( z, z'∈ C ) ならば, |fn(z')−fn(z) |<ε/3
とすることができます。したがって,三角不等式を利用して,
|f (z')−f (z)|≦|f (z')−fn(z')|+|fn(z')−fn(z)|+|fn(z)−f (z)|
≦ε/3+ε/3+ε/3 =ε
したがって,極限関数 f (z) は連続関数です。
[3]
( ステップ2 )
極限と積分の順序の交換が可能であることを示す。
f (z) および, fn(z) は連続関数なのでどちらも積分可能です。また,曲線 C の長さを L (<∞) とすれば,任意のεに対して,ある N が存在して,n>N を満たすならば,
|f (z)−fn(z)|<ε/L
とすることができます。すると,
| f (z) dz − fn(z) dz|≦ |f (z)−fn(z)||dz|
< ε |dz|=ε ( n>N のとき ) L
が成り立ちます。 (定理1の証明終)
[4]
特に, fn(z) が
fn(z) = gk(z)
f (z) = fn(z) = gk(z)= gk(z)
の形で与えられるとき,[*]式は,
左辺 = gk(z) dz
右辺 = gk(z) dz = gk(z) dz = gk(z) dz
したがって,本質的ではない記号を少し書き換えて,定理1の式は次のようにも書けます。
|
【定理2】 関数項級数に関する極限の交換
|
||||||||||||
| これは, | gn(z) が一様収束すれば, | と | とが交換可能であることを示しています。 |
証明手順から分かるように C は閉曲線でも構いません。
[1] ほぼ準備が整いましたので,テーラー展開の証明 [#] の途中で行った極限の交換,
f (z) = 1 f(t) z−a n dt ・・・ [**] 2πi (t−a) t−a
↓ 積分と級数の極限の順番を入れ代える
= 1 f(t) z−a n dt 2πi (t−a) t−a
が許されることを示していきましょう。この交換に対して,定理2を適用できることを示せば,それで証明は完了ですが,そのためには,関数項級数
gn( t ) ≡ f(t) z−a n (t−a) t−a
が一様収束することを証明できればよいわけです。
[2] そのためには次の定理を利用します。
(知っている人はパスしてもよいが,念のため。
|
【定理3 】 一様収束条件 C 上の関数列 gn(z) が, |gn(z)|≦ dn
|
||||||||
[証明]
dn に関するコーシーの収束条件から,任意のεに対してある N が存在して,N < i < j であれば,部分列について,
|gi(z) +・・・ + gj(z)|≦|gi(z)| +・・・ + |gj(z)|
< di +・・・ + dj <ε
とすることができます。したがって,i → ∞ の極限を考えるのであれば,
|g(z)−gi(z)| < ε
とすることができます。これは任意のz∈C について成り立つので,
i >N ⇒ sup |g(z) − gi(z)|<ε z∈C
| すなわち, | gn(z) は一様収束することが分かりました。 |
(定理3の証明終)
[3] 話をテーラー展開の極限交換に戻します。
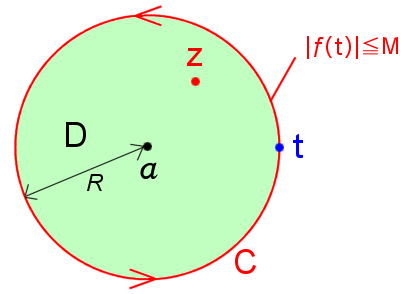
[**] 式の積分経路として,下図のような a を中心とする半径 R の円周 C を考えて,その上での正則関数|f (t)|の最大値を M とすれば,
f(t) z−a n ≦ M |z−a| n =Dn (t−a) t−a R R
| とおくと,|z−a|< R の範囲では | Dn は収束する正項級数です。 |
よって,
| 定理3 により,関数列の級数, | f(t) | z−a | n | は一様収束します。 | ||
| (t−a) | t−a |
したがって,定理2より,[**] における積分と関数項級数の極限の交換が許されることが証明できました。