| 9 ルベーグ積分の定義(2) | |
| f-denshi.com [目次へ] 最終更新日:11/07/12 最後に問題を追加 | |
| サイト検索 | |
ルベーグ積分の定義は(その1)として,すでに示しました[#]。しかし,その定義はディリクレ関数の積分には十分でしたが,関数値として,0,1以外の様々な値(連続基数)をとる関数に対しては,概念的に過ぎてそのままでは使い物になりません。ここでは,どんな関数に対しても適用な可能な形式での積分の定義を与えます。
[1] まず,単関数の積分の定義です。共通部分のない有限個の可測集合に分割可能な可測集合をXとして,
|
定義: X=A1∪A2∪・・・・・An のとき,
(2) 一般的に可測集合 E 上での積分を, と定義する。 |
1.のディリクレ関数の例で具体的に計算すれば, X = R = Q(有理数)∪ Ri(無理数)
η(x)=1・e(x,Q)+0・e(x,Ri)
となります。 そして,E=[0,1] 上の積分は,
η(x)m(dx)=1・m(Q∩[0,1])+0・m(Ri∩[0,1])
=1・m(区間[0,1]の有理数)+0・m(区間[0,1]の無理数)
=1・0+0・1
=0
[2] 単関数の積分の性質: 単関数η(x),ψ(x) について,(11/07/07 以前のコピペの残骸的数式を訂正↓)
| (1)η(x)≧ψ(x)≧0 ⇒ | η(x)m(dx)≧ | ψ(x)m(dx) |
| (2) | {αη(x)+βψ(x)}=α | η(x)m(dx)+β | ψ(x)m(dx) |
| (3) | E∩F=φ ⇒∫ | E∪F | η(x)m(dx) | = | η(x)m(dx)+ | η(x)m(dx) | ||
など。
[3] 次にこれをもとに可測関数の積分の定義を示します。
|
定義: 可測関数 f(x)≧0 の可測集合 E 上の積分とは,
とする。 ただし,上限をとる際に, 0≦η(x)≦f(x) をみたす単関数η(x)すべてについて考慮する。 |
前ページで述べておいた [#] ように,f(x)が可測関数ならば,単調増加する単関数列, 0≦η1(x)≦η2(x)≦ ・・・・ が存在して,
ηk(x)=f(x)
となります。 そこで,上極限が f(x) となるような単関数を利用して f(x) の積分を定義しようということなのです。ただし,「sup」というのが漠然としているので,「定義のための定義」であることは致し方ありません。具体的な計算方法は最後の問題を参照してください。
[4] なお,f(x) がマイナスの値をとるときは,次のように積分を定義します。
|
定義: f+(x)=Max(f(x),0 )として,可測集合 E 上の積分を定義する。
このとき,
が成り立つとき,f(x) を E 上の可積分関数と言う。 |
このf+とf-に分けて考える定義は,便宜的なもので深い意味はありません。 また,基本的な性質として次のような関係が成り立ちます。
| (1) | |f(x)|m(dx)= | f+(x)m(dx)+ | f-(x)m(dx) |
| (2) | {αf(x)+βg(x)}m(dx)=α | f(x)m(dx)+β | g(x)m(dx) |
| (3) | f(x)m(dx)= | f(x)m(dx)+ | f(x)m(dx) |
ただし,E∩F=φ
[5]
問題: 関数 y=f(x)=x の区間[0,1]における積分を単関数を利用してルベーグ積分せよ。(11/07/12)
x m(dx)
解答:
y軸(y≧0)を,積分範囲におけるf(x)の最小値,最大値を考慮し,区間 [0,1) を2n の幅で分割した,[k/2n,(k+1)/2n),k=0,1,・・・,2n-1 とそれ以上の領域に分ける。ただし,n=1,2,・・・。
すると,この区間で,f(x)=x に収束する単関数の増加列として,
|
ηn(x) = |
k/2n ←akのこと ・・・・ f(x)∈[k/2n,(k+1)/2n) ,k=0,1,・・・,2n-1 | |
| 0 ・・・・ k>2n-1 ←積分範囲外なので考えなくともよいから。 |
を選ぶことができる(下図参照)。 一方,定義域の分割は,f(x)=x の逆関数を考えて,
| f-1 | { | k | , | k+1 | |
} | = | { | x∈[0,1] ←Eのこと: | k | ≦x≦ | k+1 | ←Akのこと | } | ||
| 2n | 2n | 2n | 2n |
すなわち,x軸の領域 [0,1] は,X=A0∪・・・∪Ak-1,ただし,Ak=[k/2n,(k+1)/2n) と分割され,Akの測度(長さ)m(Ak∩E)はいずれも2-nである。よって,ηn(x)の積分値は,
|
ak・m(Ak∩E)= |
|
k | ・2-n = | 2n(2n−1) | 2-2n = | 1−2-n | ||||||||
| 2n | 2 | 2 | |||||||||||||
となる。ここで,n→∞ (supをとるということ) として,1/2 (答) を得ます。
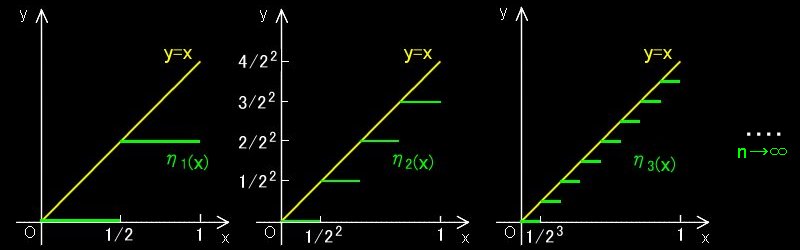
以上のようにルベーグ積分の計算は簡単な関数に対しても面倒臭いし,逆関数が初等関数でないと思考停止することも多い。
ジョルダン分解
完全加法的集合関数(測度を一般化)は,2つの測度の差として一意的に表すことができる。
F=F+−F-
ハーンの分解定理
X上の完全加法関数に対して,
F(A)≧0,F(Ac)≦0
となるA⊂Xが存在する。
ルベーグ積分は万能ではないという話
| f(x) = | sinx | = f+−f- と分解すると, | |
| x | |||
![]() f+m(dx)−
f+m(dx)−![]() f-m(dx) = ∞−∞ でルベーグ積分不可能。
f-m(dx) = ∞−∞ でルベーグ積分不可能。
一方,広義リーマン積分は可能で,
sinx dx= π x 2