A2　波動現象
f-denshi.com  更新日：　　04/10/14

１．進行波

［１］　X軸の正方向へ位相速度 v で進行する波動を考えましょう。
そのような波動u( x，t ) は，もっとも一般的に表すと，( x−vt )の関数 f として，

u( x，t ) ＝ f( x−vt )　　　　または，＝ u( x₀，t−(x−x₀)/v )

と表現することができ，次の波動方程式と呼ばれる微分方程式を満たします。

∂2u(x，t)	＝ v2	∂u(x，t)	・・・・・       [*]
∂t2		∂x2

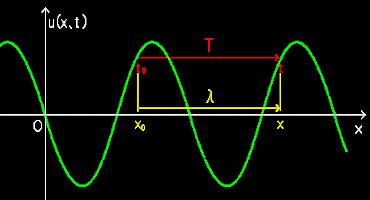
特に波形が振幅 A の正弦波である場合，時刻 t の位置 x の変位 u(x,t)は，

u(x,t)＝ f(x−vt) 　　　＝A・sin{k(x - vt)＋φ} 　　　　　　　　↓　kv＝ω　とおいて 　　　＝A・sin{kx−ωt＋φ} 　　　　　　　　↓　k＝2π/λ，　ω＝2π/T　とおいて

＝A・sin 2π kx − ωt ＋φ 2π 2π       ＝A・sin 2π kx −νt ＋φ 2π       ＝A・sin 2π x − t ＋φ λ T

と置くことができます。　波動関数に使われるパラメーターの名称と関係は以下のとおり。

A　：振幅 λ ：波長 T　：周期 k　：波数 ν ：振動数 　　(周波数) v　：位相速度 ω ：角速度 ∂ω ：群速度 ∂kmax kmax：振幅最大波の波数

ω ＝ kv   k  ＝ 2π/λ  ω/2π＝ν ＝1/T  v  ＝λν ＝ ∂ω ∂k  ω＝ 2πv/λ

［２］　３次元に拡張した場合の波動方程式は，位置ベクトルを r ＝( x，y，z ) として，

∂2u(r，t)  ＝ v2 ∂ ＋ ∂ ＋ ∂  u(r，t)　・・・・　[**]　 ∂t2 ∂x2 ∂y2 ∂z2   または， ∂2u(r，t)  ＝  ∇2 u(r，t)                          ・・・・・　　[**]'　 v2∂t2

となります。３次元になると，波動方程式の解は境界条件によって，質的に異なる解が２つ存在します。　

平面波	u(r，t) ＝ f(k ･r −ωt)
球面波	u(r，t) ＝ 1 f(k ･r −ωt) r

ここで，k ＝ (k_x，k_y，k_z) は位相の進行方向を向いた，

 |k |　　＝ 2π/λ，
ω　＝|k ||v| ＝ 2π| v |/λ＝2πν
ω² ＝ v²(k_x²＋k_y²＋k_z²) ＝ v²k²

のような関係を満たします。　　↑　1次元の場合の自然な拡張になっています。

［３］　平面波の具体的な関数形として，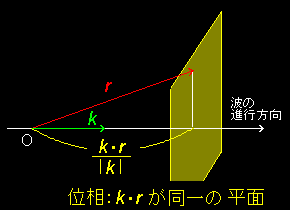　

正弦波解

u(r，t )＝A・sin{k ・r −ωt}

複素数解

u(r，t ) ＝u₀ exp [i (k ・r −ωt)]

があります。

この解を平面波と呼ぶ理由は，k が与えられたとき，ある 時刻 tで位相が等しい，つまり，k ･r ＝ 一定  を満たす空間の点(r )全体の集合が波の進行方向に垂直な平面を表すからです。

［４］　これに対して球面波は，ある時刻 t₀ で位相が等しい点全体の集合が波の進行方向に垂直な球面を表しています。

球面波についての説明は 「 グリーン関数 」を参照

［目次へ］