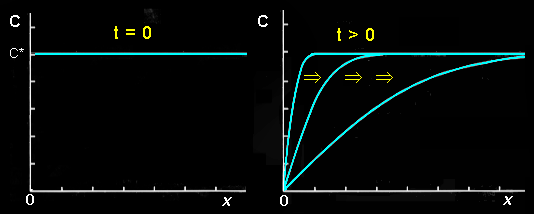|
253 拡散方程式の解法 |
|
| f-denshi.com 更新日: |
1. 拡散方程式の解法
問題
拡散方程式
| ∂C(x,t) |
= D |
∂2C(x,t) |
・・・・・ (1) |
|
|
| ∂t |
∂x2 |
|
次の境界条件のもとで解け。
時刻 t=0 において,C(x,0)=C* ・・・・・(2)
t>0 において,C(0,t)=0 ・・・・・(3)
| 位置 x= ∞ において, |
 |
C(x,t)=C* ・・・・・(4) |
|
[1] このような微分方程式の問題を解くことの物理的な意味としては,溶液中で平板電極による電解を行うときに時間変化する反応物質の溶液中の濃度分布C(x,t)に対応させることができます。すなわち,
(1)時刻,t=0 またはそれ以前における反応物質の濃度はC*で空間的に一様とし,
(2)時刻,t>0において電極に電圧が印加されると,反応物質は電極表面で速やかに化学変化を起こして消滅し,
(3)引き続く電極表面への反応物質の補給は物質拡散によってのみ支配される。
という状況にあたります。時刻 t,電極表面からの距離 x における反応物質の濃度がC(x,t)というわけです。
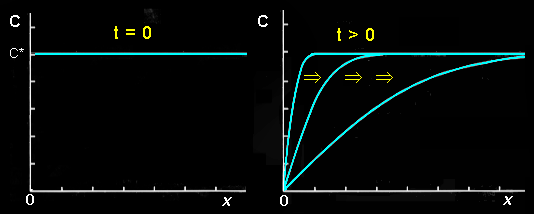
[2] この方程式はラプラス変換を利用することでスマートに解くことができます。まず,C(x,t)の変数 t に関するラプラス変換を,
 |
e-st・C(x,t)dt |
|
と書くことにすると,拡散方程式(1)は,変数 t に関するラプラス変換(t→s)によって,
|
|
|
←公式 L[f’(t)]=sF(s)−f(0)を用いてます[#]。 |
|
| ∂x2 |
となります。 また,境界条件(2)は,
と書くことができます。
[3] さらに,C(x,s)の x に関するラプラス変換を,
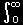 |
e-yx・C(x,s)dx |
|
とすると,(5)の x に関するラプラス変換(x→y)は,
↓公式,L[f”(x)]=y2F(y)−yf(0)−f’(0)を用いて[#],
となります。これを整理すると,y を含まない関数,α(s),β(s),γ(s)を用いて,
|
|
α(s) |
+ |
β(s) |
+ |
γ(s) |
・・・ [*] |
|
|
|
| y |
{y+(s/D)1/2} |
{(y−(s/D)1/2} |
とあらわされます[#]。この式をラプラス逆変換で,y から x の関数に戻すと [#],
|
|
・・・・・(6) |
| C |
(x,s)=α(s)+β(s)exp{−(s/D)1/2x}+γ(s)exp{(s/D)1/2x} |
となります。 ↑ 公式 L-1[1/(s+a)] = exp{-at} を使いました。
[4] ここで,境界条件(4)を t に関してラプラス変換した次式,
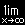 |
|
C* |
|
| s |
を(6)式に要請すると,α(s)=C*/s,かつ,γ(s)=0 でなければなりません。したがって(6)は,
|
|
|
| C |
(x,s)=C*/s+β(s)exp{−(s/D)1/2x} |
←境界条件(2),(4)の元で成り立つ |
[5] さらに,境界条件(3)をラプラス変換した,
を要請すると,(6)において,β(s)=−C*/s も満足しないといけません。結局,
|
|
|
| C |
(x,s) |
=C*/s−(C*/s)・exp{−(s/D)1/2x} |
|
これを逆変換で s から t の関数に戻すと,
| C(x,t)=C*=C* |
 |
1−erfc |
 |
x |
  |
|
|
|
 |
4Dt |
ここで,誤差関数:
| erc{h}= 1−erfc{h}= |
2 |
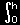 |
exp{-u2}du |
|
|
|
 |
π |
|
を用いています。この関数はいろいろな分野で重要な関数で非常に良く調べられています。
| erc{h}= |
2 |
 |
x− |
x3 |
+ |
x5 |
− |
x7 |
+ |
x9 |
− ・・・ |
 |
|
|
|
|
|
|
|
 |
π |
|
3 |
5・2! |
7・3! |
9・4! |
| ≒ |
2x |
( x << 1 ) |
|
|
|
 |
π |
|
誤差関数について,
[目次へ]
|
|
|
| Γ(1/2)= |
 |
π |
(注意) [*]の導出を丁寧に書くと,y の関数と見て次のように変形します。
| = |
|
|
| y{y+(s/D)1/2}{(y−(s/D)1/2} |
| = |
α(s) |
+ |
β(s) |
+ |
γ(s) |
|
|
|
| y |
{y+(s/D)1/2} |
{(y−(s/D)1/2} |
ここで,α(s),β(s),γ(s)は,最後の式を通分して,その上の式と比較すれば具体的に求めることができます。しかし,今問題を解くためにそこまでする必要はありません。