 |
204 フーリエ積分定理 |
| f-denshi.com 更新日: |
具体的な使い方を追加すること
1.フーリエ積分定理
[1] フーリエ変換と内容は同じなのですが、三角級数展開を用いた形式についても述べておきましょう。
もう一度、フーリエ三角係数、an、 bn を、
| an= |
1 |
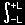 |
f(t)cos |
nπt |
dt、 bn= |
1 |
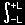 |
f(t)sin |
nπt |
dt |
|
|
|
|
| L |
L |
L |
L |
として、区間 [-L、L ] でf(x)のフーリエ級数展開を書き下ろすと、
| f(x)= a0/2 + |
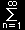 |
{ ancos |
nπx |
+ bn sin |
nπx |
} |
|
|
| L |
L |
↓ an、 bn 代入
| = |
1 |
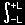 |
f(t)dt + |
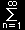 |
1 |
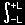 |
f(t){ cos |
nπt |
・cos |
nπx |
+ sin |
nπt |
・sin |
nπx |
} dt |
|
|
|
|
|
|
| 2L |
L |
L |
L |
L |
L |
↓ 加法定理
| = |
1 |
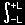 |
f(t)dt + |
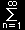 |
1 |
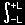 |
f(t)・cos |
nπ |
(t−x)dt |
|
|
|
| 2L |
L |
L |
ここで、f(x)が[−∞、∞]において定義されているとし、L → ∞ の極限を考えれば、上の第一項のf(t)積分が有限ならば、第一項全体は
0 に収束し、第2項は、
| f(x) = |
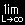 |
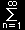 |
1 |
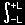 |
f(t)・cos |
nπ |
(t−x)dt |
|
|
| L |
L |
↓
| = |
1 |
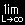 |
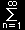 |
π |
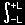 |
f(t)・cos |
nπ |
(t−x)dt |
|
|
|
| π |
L |
L |
↓ 上式は、刻み幅π/Lとしたリーマン積分の定義とおなじですね。
| = |
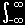 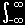 |
f(t)・cosλ(t−x)dt dλ |
この式をフーリエ積分定理と言います。
[2]
|
フーリエ重積分定理
| f(x) = |
1 |
 |
 |
f(t)・cosλ(t−x)dtdλ |
|
| π |
(複素形式)
| f(x) = |
1 |
 |
dλ |
f(t)・exp [iλ(t−x)] dtdλ |
|
| 2π |
フーリエ単積分定理
| f(x) = |
1 |
 |
f(t)・ |
sinλ(t−x) |
dt |
|
|
| π |
t−x |
|
[目次へ]