| 3 連続関数と微分可能性 | ||
| f-denshi.com [目次] 最終更新日: | ||
| サイト検索 | ||
[1] ある区間 M 上の点 a において,「関数 f(x)が a で連続である。」 とは,
「 a に近づく任意の点列: x1,x2,・・・xn,・・・ に対応する像の点列: f(x1),f(x2),・・・,f(xn),・・・が f(a) に収束する。 」
⇔
「 xn → a のとき, f(xn) → f(a) 」 ← 簡単にはこう書きます。
ということになります。ε-δ論法を使うならば,
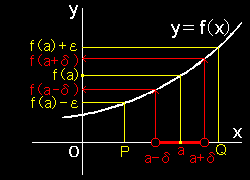 (1) 点 a で連続: (1) 点 a で連続:どんな正数εをとってもある正数δが存在して, 0<|x−a|<δ ⇒ |f(x)−f(a)|<ε が成り立つとき, 「 関数 f(x)は a で連続である 」 (2) 区間 M で連続: 区間 M のすべての点で関数f(x) が連続であるとき, 「 f(x)は Mにおける連続関数である。」 と言います。 |
[2] 連続関数の中で特に与えられたεに対して点 a に依存しないδ,つまり,考えている区間 M において共通して使える δを一つ定めることができるとき,この関数はその区間で一様連続な関数であるといいます。厳密に書くと,次のようにいえます。
| 一様連続: どんな正数εをとってもある正数δが存在して, 0<|b−a|<δ ⇒ |f(b)−f(a)|<ε が区間 M の任意の点 a,b について成り立つ。 |
[4] 連続関数のもっとも基本的な特徴を2つ挙げておきましょう。
| 定理 (1) 閉区間[a,b]で定義された連続関数は有界であって最大値と最小値を取る。[ 最大値の定理 ] (2) 閉区間[a,b]で定義された連続関数はこの区間上で一様連続である。 |
[ 証明 ] (1)
(ステップ I ) 連続関数 f(x)は有界である⇔上限 M,(下限 m )をもつことを背理法で示します。
f(x) が上に有界でない と仮定すると,f(p0)=r >0 なる点 p0 が必ず [a,b] に存在します。さらに,f(p1) > 2f(p0) なる点 p1 が存在し,同様にして,
0 < r < f(p0) < f(p1) < ・・・・ < f(pn) < ・・・・ ,ただし,f(pn) > 2n・f(p0)
を満たす無限の点列 {pn} が閉区間 [a,b] の中に存在し,この区間に集積点をもちます[#]。
そこでその一つを P とし,{pn} からとった P に収束する部分列を { P1,P2,・・・・ } とします。すると,f(x) が連続関数であることから,k→∞ のとき,f(Pk) → f(P) と収束しなければなりません。ところが,
f(Pk) ≧ f(pk) > 2k・f(p0)
なので,f(Pk) は k→∞ で発散します。矛盾! よって,f(x)は上に有界で上限 M をもちます。下限の存在も同様です。
(上限・下限[#]の存在と最大値・最小値の存在は別なのでステップ2の証明が必要です)
(ステップ II ) f(p) = M なる p ∈ [a,b] が存在することを背理法で示します。
もし,どんな p ∈ [a,b] についても,f(p) ≠ M であるならば,関数: F(x) = 1/(f(x)−M) はこの閉区間で連続関数となります。ところが,上限の定義から f(x)−M はいくらでも 0 に近づけることができる,これは,|F(x)|がいくらでも大きくなり,有界でないことを示しています。これはステップ I に矛盾します。すなわち,f(p) = M となる p が閉区間 [a,b] に存在する,言い換えると,p において最大値M をとることがわかりました。最小値の存在も同様です。
この定理は,定義域を一般化(抽象化)された閉集合に拡張して,
(1)' 閉領域 M で定義された連続関数は有界であって最大値と最小値を取る。
(2)' 有界閉領域 M 上の連続関数はこの領域で一様連続である。
と述べることができます。
[証明] (1)',(2)' 一般化された最大値の定理は集合論の中で説明しています ⇒ [#]
[1] 前置きが長くなりましたが,いよいよ微分の定義です。
|
f(x)を定義域 M で定義された関数とする。このとき,極限値 が存在するとき,「 f(x)は点 a で微分可能 」といい,その値を微分係数と呼び, f'(a) と書く。 |
もう少し丁寧に言うと,h を正数として,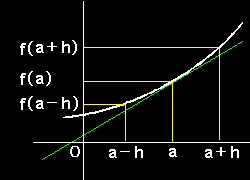
f(a+h)−f(a) ; a∈M h
が存在するとき,「 f(x)は点 a で右から微分可能 」といい,その値を右からの微分係数と呼び, f'+(a) と書きます。さらに,
f(a-h)−f(a) ; a∈M -h
が存在するとき,「 f(x)は点aで左から微分可能 」といい,その値を左からの微分係数と呼び, f'-(a) と書きます。そして,
f'+(a) =f'-(a)
のとき, f(x)は点 a で微分可能 」といい,その値を微分係数と呼び, f'(a) と書きます。
[2] 上の定義は一点 a に置ける微分可能性について述べたものですが,ある区間 M の任意の点 a について微分可能であるとき,a を変数らしく x と書いて,導関数 f'(x)と書きます。もちろん,x∈M。また,微分係数の別の表現として,
微分係数Aの定義 : 適当な定数A が存在して, h→0 ⇒ f(a+h)−f(a)=Ah + o(h)と書ける。
といった表現も使われます。o(h)は h より高位の無限小である任意のh の関数です[#]。
[3] 連続関数と微分可能な関数との関係
| 定理 ある区間M で定義された関数f(x)が微分可能ならば,この区間でf(x)は連続である |

関数f(x)が点a∈Mで微分可能ならば,適当な定数A が存在して,
h → 0 ⇒ f(a+h)−f(a) = Ah + o(h)
したがって,
h → 0 ⇒ f(a+h)−f(a) → 0
[4] この定理の逆は成り立ちません。連続でも微分できない関数は無数にあります。いくつか例を挙げておくと,
(1) fn(x)=
xnsin 1 ( x≠0 ) x 0 ( x =0)
を考えます。ただし,n=1,2,・・・とします。すると,
xnsin 1 < |xn| x
より,fn(0)=0 とすれば,fn(x)は,n=1,2,・・・ において連続関数ですが,
x=0 における微分可能性は,
f'n(0)= 微分不可能 (n=1) 0 (n≧2)
となります。 ⇒ 証明 [#]
もっと,極端な例としては,”いたるところで微分不可能な連続関数”なんかも見つかっています。
| (2) f(x)= | ancos(bnπx); 0<a<1, b:奇数, ab>1+(3π/2) [ワイエルストラウス] |
| (3) f(x)= | 2-nsin(2nπx) [セレリエ] |
(4) フォン・コッホ曲線
参考:
「数学100の発見(数学セミナー編集部偏)」,p.159,奇妙な曲線,松本一信,日本評論社(1998年).
[5] 関数の微分公式を2つここで書いておきましょう。
合成関数の微分公式です。 z(x)=z(y(x)), のとき,
dz = dz ・ dy dx dy dx
[6] 逆関数の微分公式
dy = 1 dx
dx dy
[1] 関数f(x)に導関数が存在する場合,その導関数について再び微分可能性を議論できます。導関数に導関数が存在する場合,それを2階導関数,または2次導関数といいます。さらに一般化して高い次数のn階導関数を考えることもできます。
身近な関数:有理関数,三角関数,指数関数など,たいていの関数は無限階微分可能です。すると,1回微分可能ならば,何回でも微分可能でないかと思いたくなりますが,1回微分可能でも2回目はダメというのはいくらでもあります。たとえば,次の関数です。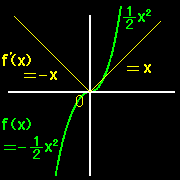
y =
x2 2 (x≧0) −
x2 2 (x<0)
を微分すると,
y'= x (x≧0) −x (x<0)
ですが, y'(0)=0 (y'=傾き0)で,y' は x=0 で滑らかにつながっているので連続関数です。しかし,この関数 y'は,x = 0 でトンガっている(上図)ので,y”は存在しないことがわかります。こういった関数は熱力学で2次相転移を記述するときにでてきます。ルーチン的にこのような関数をいくらでも作る方法があるのですが,それは積分を勉強してからにしましょう。⇒[#]
[1] まず,この定理を書きましょう。
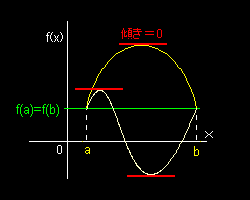
| [ ロルの定理 ] 閉区間[a,b]で定義された関数f(x) が, (1) 閉区間 [a,b] で連続 (2) 開区間 (a,b) で微分可能 (3) f(a)=f(b) ならば, f '(a+θ(b−a)) = 0 となる θ(0<θ<1) が存在する。 |
この定理の意味するところは,”高さ”の等しい2点A,B を結ぶ滑らかな連続曲線を考えると,傾きが0 となる点が,A とB の間に少なくとも一つは存在することをいっています。下図で言えば,黄色の曲線では一箇所,白い曲線では二箇所傾き0 の点があります。
この定理でいう閉区間とはもちろん実数の集合をさしています。条件(1)はそういう意味も込めて連続と言っているのです。そうでないとこの定理が成立しないことは,例えば,
関数: f(x) = -x(x+2)(x−2) を [-2,2] で考え,微分すると, y'= -3X2+4
なので,有理数の集合の中だけで考えていたのでは極値をとるときの x の値を見出すことができません(図B)。
(こんなところでも実数の連続性[#]が活躍しているのです!)
(2)の微分可能性の意味することは,もし,微分可能でない点,つまりとがった点が存在すると,傾き
0 の点は必ずしも存在しないと言ってるのです。これも下の図 C をみれば,一目瞭然でしょう。
 |
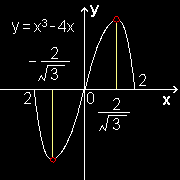 |
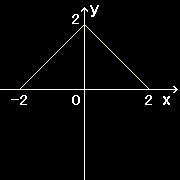 |
| (A)ロルの定理 | (B)連続でないとき | (C)微分可能でないとき |
ロルの定理の証明:
閉区間 [a,b]で,f(x)=定数のときは,この区間で f'(x)=0 なので,定理が成り立つのは明らか。そこで,f(x)は定関数ではなくある点でf(x)>f(a)=f(b)なる点が存在する場合を考えます。このとき,最大値の定理より,閉区間 [a,b]のある点p=a+θ(b−a) でf(x)は最大値をとり,任意のh>0に対して,
f(p+h)−f(p)≦0
両辺hで割って,h→0とすれば,これは右からの微分係数について,
f'+(p)≦0
であることを意味します。今度は,
f(p−h)−f(p)≦0
について(-h)で割って,h→0とすれば,左からの微分係数について,
f'-(p)≧0
が示せます。今,f(x)は微分可能なので,左右からの微分係数は一致するはずです。これが成り立つのは,
f'+(p)=f'-(p)=0
のときだけです。つまり,f(p)=0 であることがわかりました。
f(x)<f(a)=f(b)なる点が存在する場合も最小値の定理を用いて,f'(q)=0 となる点q が存在することを同様に示せます。
| [ 平均値の定理 ] 閉区間[a,b]で定義された関数f(x)が, (1) 閉区間[a,b]で連続 (2) 開区間(a,b)で微分可能 ならば, となる θ(0<θ<1) が存在する。 特に,b=a+h と書き直せば, f(a+h)=f(a)+hf '(a+θh) |
この定理はロルの定理で傾きが0 であるところを ”任意の高さにある A,B の傾き” に拡張したものです。証明もロルの定理と変わりませんので省略します。
[1] 連続関数のかかわる重要な命題をいくつか挙げておくと,
|
(1)単調な連続増加関数には逆関数が存在する→[#]。 ← 中間値の定理を使う (2)ペアノ曲線:連続写像f: [0,1]→[0,1]×[0,1] は存在するが,f: [0,1]→{[0,1]×[0,1]−p0}は存在しない→[#] (3)内接する多角形の面積を最大にする条件を求める証明 →[#] (4)ヒルベルト空間(無限次元の場合)では有界な閉集合でも最大値・最小値をもたない。→[#] (5)閉区間 [a,b] で定義された連続関数は有界であって最大値と最小値を取る。[最大値の定理]→[#] (6)閉区間 [a,b] で定義された連続関数はこの区間上で一様連続である。→
[#] |
などなど。