| t104 カノニカル分布の導出 | |
| f-denshi.com 更新日:13/07/11 | |
| サイト検索 | |
| 目次へ | |
熱力学において,定温,定圧,定積などの実験条件に合わせて様々な自然な変数をもつ熱力学変数(関数)が定義されたように,統計力学においても考察すべき対象によっては,ミクロカノニカルアンサンブル(小正準集団)で用いられるエネルギー E,粒子数 N,体積 V の組合わせ以外の変数を用いた方が便利な場合があります。特に系の粒子間に相互作用が存在し,系のエネルギー,状態数が具体的に表せない場合はエネルギーの代わりに温度を用いた取り扱いが便利です。ここではミクロカノニカルアンサンブルをベースにボルツマン因子をもつカノニカル分布(正準分布)を導出します。
[1] ミクロカノニカル分布では,粒子数N,全エネルギー E,体積 V を変数として議論が展開されましたが,実験室では温度Tを変数にとる方が便利というだけでなく,微視的状態のエネルギーを具体的に記述できない場合があります。そのようなときの取り扱いを可能とする方法がカノニカルアンサンブル(正準集団)の方法と呼ばれるものです。この方法はミクロカノニカルの方法とは異なる考え方のようですが,理論的拠り所はミクロカノニカルアンサンブルと同様にエネルギー一定である孤立系に対する等重率の原理とボルツマンの原理に基づいています。
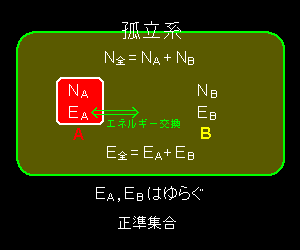
孤立系である全系を2つの部分,系A と 系B に分けて考える事とします。ただし,系A と系B 間は熱だけを透過する透熱壁で遮られており,熱エネルギーは交換するが,粒子は交換できないとします。また,系Aは系Bに比べて非常に小さく,系Aを部分系,系Bを熱力学でもしばしば利用される熱浴と呼ぶことにします。そして,部分系だけに観測対象を制限すると,それが,N,T,Vを変数に用いるカノニカル分布が導かれます。
全系の全エネルギー,全粒子数は各系A,Bそれぞれの和であらわすことができ,
NA,NB,N全 一定 (1)
EA+EB = E全 一定 (2)
を満足するとします。ここで時間経過に対して,NA,NB は一定とします。一方,EA,EBは透熱壁を通して,エネルギーを交換するために,熱的なゆらぎが存在し,いろいろな値を時々刻々とり得ると考えますが,EA<<EB は満たされているとします。また,各系の状態数は粒子数,体積の関数でもあり,WA(EA,VA,NA),WB(EB,VB,NB) と書くべきですが,ここでは,どちらの粒子数も体積も,透熱壁で固定されているので,以下の計算式中ではVA,VBとNA,NB は省略します。
微視的状態 (++--・・・+-+-・・・・) = (++--・・・) ∩ (+-+-・・・・) 全系 系A 系B |
 |
|||||||||||||||||||||
[2] 全系 (孤立系) の状態の中で,系A (考察対象) がエネルギーEAを持っており,さらに,残りの系B (熱浴) がEBを持つような状態数W全(EA∩EB)は系Aの微視的状態数WA( EA)と系Bの微視的状態数WB(EB)との積,
W全(EA∩EB)=WA( EA)×WB(EB)=WA( EA)×WB(E全−EA) (3)
で表されます。すると,全系の状態数W全(E全)は上式の中で, EA+EB=E全 (一定) を満たすものをすべて拾い出して,和をとればよいので,
W全(E全)= Σ W全(EA∩EB) = Σ WA( EA)×WB(E全−EA) (4) EA+EB=E全 EA
で表されることになります。右辺の和は取り得るすべてのEAに対してとります。また,等重率の原理から全系の微視的状態の一つひとつの出現確率はすべて等しく,1/W全(E全)であるとの仮定をおくのは,ミクロカノニカルの方法のときと同様です。
特に,系Aの微視的状態の一つ r だけに着目し,その微視的状態の系AのエネルギーをEr (=EA)と書くことにします。すると,等確率で出現する全系の微視的状態の中で,系Aが微視的状態rにある個数は,
W全(Er∩(E全−Er))=1×WB(E全−Er) ( =WB(EB) )
であることがわかります。すなわち,系Aが微視的状態rであるような全系の状態数は,熱浴である系Bがエネルギー (E全−Er) である状態数に等しい。すなわち,部分系Aが微視的状態rである確率は,
Pr= W全(Er∩(E全−Er)) ← 等重率の原理から W全(E全)
= WB(E全−Er) ∝ WB(E全−Er) (6) W全(E全)
となり,そのときの熱浴の微視的状態数に比例することがわかります。
[3] 次に,ボルツマンの原理 S(E)=k log W(E) を用いると,右辺の状態数は
WB(E全−Er) = exp SB(E全−Er) ・・・・・[*] k
とエントロピーと関係付けられます。さらに,E全>>Er (=EA) に注意して,指数の肩の分子,S(E全−Er) をテーラー展開すると,
SB(E全−Er) ≒ SB(EB=E全)+ ∂SB(EB) EB=E全 (−Er) ∂EB
= SB(E全)− Er TB(E全)
= SB(E全)− Er (7) T
と変形できます。途中で熱力学公式,
∂S = 1 ∂U V,N T
をE≡Uとみなして用いました。また,熱浴の温度TB(E全)を全系の温度Tに等しいとしています。厳密には,熱浴は系Aとのエネルギーのやり取りによって温度も揺らぐはずですが,「系A<<熱浴」の状況下では,それを観測できないと考えます。よって,(7)を[*]に代入して,
WB(E全−Er) ≒exp SB(E全) ・exp − Er ( ∝ Pr ) (8) k kT
[4] さらに,1つ目の指数項は状態rに依存しない定数なので,確率の規格化定数Zに含めてしまえば,
Pr= 1 exp − Er Z kT
と書くことができます。このZは分配関数と呼ばれで,
Z= exp − Er kT
を計算することで得られます。以上が温度Tの熱浴に接している系において,エネルギーErをもつ微視的状態 r が実現する確率((離散的な)カノニカル分布(正準分布))となります。
平衡温度
全系が熱平衡にあり,そのときの系AのエネルギーがE*Aならば,W全(E*A∩E*B)=W全(E*A∩(E全−E*A)は最大確率分布[#]となっており,それは対数をとっても同様であり,
k log W全(EA∩EB) = k log [WA( EA)×WB(E全−EA)]
= SA(EA)+SB(E全−EA)が極値をとる条件と一致します。すなわち,
∂k log W全(EA∩EB) = ∂SA(EA) + ∂SB(E全−EA) ・ ∂EB =0 ∂EA EA=E*A ∂EA ∂EB ∂EA EA=E*A でなければなりません。よって,EA+EB=E全(定数) に注意すれば,平衡状態では,
∂SA(EA) = ∂SB(EB) ・・・・・ [*] ∂EA EA=E*A ∂EB EB=E*B となっているはずです。ここで,熱力学公式,
∂S = 1 ∂U V T を参考に,系のエネルギーEと熱力学の内部エネルギーUを同一視して,エントロピーのエネルギーによる微分を統計力学的温度として定義すれば,先ほどの等式[*]の熱力学的意味は,
1 = 1 TA(E*A) TB(E*B) と考えられます。すなわち,平衡状態において2つの系の温度は等しくなければならない。この温度を
TA(E*A)=TB(E*B)≒TB(E全)≡T と書くことにします。
次に1.の結果を連続確率変数を用いた表現に書き直しましょう。
[1] 連続確率変数の場合の確率は,確率密度を着目する積分範囲で積分することで求まります。すなわち,系A のエネルギーがEAとEA+ΔEAとの間にある確率ということであれば,確率密度f(EA)を用いて[#],
p(EA≦E≦EA+ΔEA) = EA+ΔEA f(E)dE ≒ f(EA)ΔEA (11) EA
と定義することができます。もちろん,≒は,ΔEAは小さいとしての近似。(ただし,いつもΔEAが小さくなければならない数学的必然性はありません。)
[2] また,全系 (孤立系) の状態の中で,系A (考察対象) がエネルギーEAを持っており,残りの系B (熱浴) がEBを持つような状態数W全(EA∩EB)は系Aの微視的状態数WA( EA)と系Bの微視的状態数WB(EB)との積,
W全(EA∩EB)=WA( EA)×WB(EB)
で表されることは離散変数のときと同じです。ただし,連続変数の場合,(11)式同様に積分範囲の幅である,ΔEA,ΔEBも指定してやる必要があるので,
WA( EA) → WA(EA,ΔEA)
WB(EB) → WB(EB,ΔEB)
と表記する方が正確です。すると,全系(孤立系)のエネルギーがE全である全系の状態数をW全(E全)とすると,EA+EB=E全(一定) の下で,
p(EA ≦E≦ EA+ΔEA )
≒ f(EA)ΔEA = W全(EA∩EB) = WA(EA,ΔEA)WB(EB,ΔEB) W全(E全) W全(E全)
∝ WA(EA,ΔEA)WB(EB,ΔEB) ・・・・・・・ [**]
のような比例関係がわかります。ここで,状態数についても連続変数として扱うため,エネルギーの関数である状態密度Ω(E)を導入して,
WA(EA,ΔEA)=W(EA ≦E≦EA+ΔEA)
= EA+ΔEA ΩA(E)dE ≒ ΩA(EA)ΔEA EA
と表し,さらに,系Bの状態数に関しては,ボルツマンの原理を適用して,(8)を導いたように[#]
WB(EB,ΔEB) = exp[SB(E全-EA,ΔEB)/k) ] ∝ exp − EA kT
と変形すれば,[**]は,
f(EA)ΔEA ∝ ΩA(EA)exp − EA ΔEA kT
と書くことができます。ここで,注意しなければならないことは,確率密度と状態密度を混同しないことです。
[3] すなわち,確率の規格化定数Zを用いて,確率密度は,
f(EA) = 1 ΩA(EA)・exp − EA Z kT
とすればよいことがわかります。ここで,Zは,
f(EA)dEA =1 EA
を満足するように定めます。積分範囲は系AのエネルギーEAが取り得るすべての値にわたります。
Z(T,V,N) = ΩA(EA)・exp − EA dEA すべてのEA kT
この Z を分配関数といいます。
なお,EA<<EB≦E全と近似しているので,EAは∞を含めたすべてのエネルギー値について積分するわけにはいけないのですが,f(EA)は指数関数的に0に近づくので,実際は,積分上限を∞としても結果は変わりません。
以上,記号を EA→E と改めてまとめると,
| カノニカル分布(正準分布)と分配関数 温度 T において,ある微視的状態が (エネルギーE) をとる確率密度f(E) ,または微視的状態rをとる確率prは状態rのエネルギーをErとして, ただし,Zは分配関数で, または, で表される。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ヘルムホルツ自由エネルギー
[1] 分配関数から導かれる統計力学的?熱力学関数について述べておきます。まず,やや天下り的だが,先人の試行錯誤の成果をそのまま有難く頂戴することとし,はじめから分配関数の対数,
logZ(T,V,N) =log exp − Er kT
を考えます。ここで,β=(1/kT) とおいて,βで微分すれば,
∂log Z = 1 ・ ∂Z =
−Er exp [−βEr ] =− Erpr = −<E> (31) ∂β Z ∂β Z
これはエネルギーの期待値にマイナス符号をつけたものです。一方,(31)の左辺は,
∂ = ∂ =−kT2 ∂ ∂β ∂(1/kT) ∂T
とも書けることから,
<E>=kT2 ∂log Z ∂T V,N
これより,(31)は,
∂ −kTlog Z =− <E> ∂T T T2
と変形することができます。これを熱力学におけるギブス−ヘルムホルツの関係式[#],
∂ F = − U ∂T T V,N T2
と比較すると,( もちろん,U = <E> と考える )
F ⇔ −kT log Z
なる対応があることに気がつきます。そこで,⇔ を = として,この量を統計力学的ヘルムホルツ自由エネルギーまたは,単にへルムホルツ自由エネルギーと定義して熱力学のそれと同一視します。
F = −kT log Z(T,V,N) = −β-1 log Z(T,V,N) [ヘルムホルツ自由エネルギー]
これは,系の分配関数ZをT,V,Nの関数として求めることができれば,ただち,上式からヘルムホルツ自由エネルギーが計算でき,さらに,熱力学公式,
dF=−SdT−PdV+μdN
より,
圧力,エントロピー,化学ポテンシャルは,
P = − ∂F T,N = kT ∂log Z T,N = β-1 ∂log Z β,N ∂V ∂V ∂V
S = − ∂F V,N = k ∂Tlog Z V,N = −kβ2 ∂β-1log Z V,N ∂T ∂T ∂β
μ = ∂F V,T = −kT ∂log Z T,V = −β-1 ∂log Z β,V ∂N ∂N ∂N
これらに加えて,再掲しておくと,
U =kT2 ∂log Z =− ∂log Z ∂T V,N ∂β
が計算できます。これはすべて微分するだけですから,簡単な計算ですね。結局一番大変なのは最初に分配関数を計算するところです。その次に熱力学関数たちを適切な独立変数で表示してやるところも計算が大変です。
P(T,V,N)=− ∂F ∂V T,N Z(T,V,N)
分配関数⇒ F(T,V,N)=−kTlogZ
自然な変数→
S(T,V,N)=− ∂F ∂T V,N →
U(T,V,N)=kT2 ∂logZ ∂T V,N ↓ ↓T について解いて ↓
μ(T,V,N)= ∂F ∂N T,V
T=T(S,V,N)
Cv= ∂U ∂T V,N ↓ U=F+TS U(S,V,N)
自然な変数
とりあえず,ここまで。
SUSTAINABLE TOKIWADAIGAK SINCE 2002
統計力学 I