| t101 2つ原理とミクロカノニカルアンサンブル | ||
| f-denshi.com 更新日: 13/07/11 | ||
| サイト検索 | ||
| 目次へ | ||
はじめに統計力学の考え方に慣れ親むために,一つひとつの粒子は2つのエネルギー(固有)状態しかとりえない,粒子間相互作用のない「2準位系」を取り上げて,「ミクロカノニカルアンサンブル(小正準集団)の処方」を実際に体験してみましょう。「習うより慣れろ」ということです。
[1] ニュートン力学の「3つの運動の法則」に相当するような統計力学の基本原理は2つあります。それは,
1.等重率の原理
2.ボルツマンの原理
です。1つ目の等重率の原理とは,統計力学的な考察の対象となる孤立系[#]の微視的状態の総数をWとすれば,その微視的状態の一つ「r」(←状態を区別するためにつけられた通し番号)が観測される確率=出現確率はどれも等しく,
pr= 1 W
であるとするものです。この等確率で観測されるという微視的状態の集合をミクロカノルアンサンブル(小正準集団)といいます。形式的ですが,後の別のアンサンブルとの整合性を取るために,微視的状態の総数を,
W(N,V,E)= 1
と表記しておきましょう。ここで,rに関する和は,すべての微視的状態にわたってとることとします。また,孤立系の粒子数N,体積V,エネルギーE,これらを変数として,系が特徴付けられるとしています。
上の説明をはじめて聞いた人は何のことだかよくわからない人もいることでしょう。特に,運動エネルギーのように連続的に変化すると考えられるエネルギーをイメージしていては微視的状態の数とは何なのか,どうやってそれを数えるのか思いつきません。実際,それは難しい話です。(しかし,そこから統計力学の話をスタートさせる教科書,講義が多い。困ったものだ!) そこで,ここでは下に示すような,1つの粒子がとることのできる「1粒子エネルギー」として,2つの値,±εしか取りえないような最も単純な2準位系を例にとって説明していきましょう。連続的な物理量を含む話は後回しです。
[2] この2準位系は多数のN個の粒子から構成され,低いエネルギー準位(-ε)にあるものがN1個,高いエネルギー準位(+ε)にあるものがN2個である孤立系とします。つまり,
全粒子数 N=N1+N2 ・・・・・(1)
全エネルギー E=ε(N2−N1) ・・・・・(2)
という関係が成り立っていることとします。この系が孤立系であれば,外界との相互作用はなく,また,粒子間相互作用,体積依存性も考えません。
系が(1),(2)を満足する平衡状態にあるとき,粒子一つひとつのエネルギー固有値(±ε)が完全に指定された「微視的状態」は多数存在しますが,ある一瞬を取り出したとき,それらの中のどの状態が実際に実現しているかは等確率であると仮定するのが等重率の原理です。
イメージ
Nは一般的にはアボガドロ数オーダーの大きな数で,そのようなときに統計力学的な考え方は意味を持つのですが,説明の都合上,N=4,N1=3,N2=1,E=-2ε の系を下図に示しておきます。孤立系におかれた,a,b,c,d,4つの粒子の中で,1粒子だけが高い準位にあり,残り3つが低い準位にあれば,E=-2εを満たします。そのような微視的状態は,図に示した4つが考えられ,系はこの4つ微視的状態間を素早く移り変わる(遷移)ものとします。そのため,この系を観測したとき,どの状態が実際に見出されるかは「どの状態についても確率1/4である」と先験的に,つまり証明抜きでこれを認めます。これが等重率の原理と呼ばれるものです。ここで,各微視的状態の出現確率が4分の1であることは,巨視的観測値とみなされる統計平均や期待値を計算するときに利用されます。系が微視的状態の間を素早く遷移する理由については最終的には量子力学の知識が必要です。
(2準位系の具体的なイメージとしては,磁場H中におかれた多数の電子スピンからなる系などがあるが,ここでは一般性を持たせてεのまま説明する。また,「固有状態」という言葉は量子力学的に取り扱う場合に用いられるものであるが,ここでの議論は量子力学的な効果を考慮する「量子統計」に基づくものではない。)
[3] さて,粒子数Nの場合に話を戻すと,微視的状態数WはN個の粒子の中からN1個を下の低い準位に割り当て,残りN2個を自動的に上の高い準位に割り当てる組み合わせ数を計算すればよく,次式で与えられます。
W=NCN1= N! ・・・・・(3) N1!N2!
さらに,(1),(2)式をN1,N2について解いて得られる
(εN−E)/2ε=N1
(εN+E)/2ε=N2
を(3)に代入し,WからN1,N2を消去します。すると,NとEを与えたときに等確率で現れる微視的状態数Wは次式となります。
W(E,N)= N! ・・・・・(4) ((εN+E)/2ε)!((εN−E)/2ε)!
この系では体積依存性を考慮しませんが,より一般的には,体積も変数に含むW(E,V,N)を求めることがミクロカノニカルアンサンブルを用いる統計力学的扱い(以後,ミクロカノニカルアンサンブルの方法と呼ぶことにします) の最初の作業となります。
[4] 次に導入する統計力学の基本原理は,この微視的状態数と熱力学体系を直接結び付けている関係式で,ボルツマンの原理と呼ばれ,次式で与えられます。
S(E,N)=k log W(E,N) ボルツマンの原理
体積を考慮する必要がある場合は,S(E,V,N)=k log W(E,V,N) です。
これは統計力学的エントロピーSの定義とされます。しかし,統計力学的とはいっても,熱力学に登場するエントロピーに正確に対応していると考えて(仮定して),理論展開されていきます。ボルツマンの原理も等重率の原理と同様に証明すべきものではなく,物理法則として無条件で受け入れるべき統計力学の「基本原理(数学における公理)」です。微視的状態の対数とエントロピーとの比例定数「k」はこの関係式の発見者の名をとってボルツマン定数と呼びます。
さて,(4)を「ボルツマンの原理」の式に代入すれば,この系のエントロピーS(E,N) がわかります。すなわち,
S=klogW
=k{ logN!−log(εN+E)/2ε)!−log(εN−E)/2ε)!}
これでもよいのですが,後々の計算の便を考え,Nが大きな数であるときに成り立つ近似,
logN!≒NlogN−N [近似公式]
を用いて,
S/k≒NlogN−N−((εN+E)/2ε)log((εN+E)/2ε)+(εN+E)/2ε
−((εN−E)/2ε)log((εN−E)/2ε)+(εN−E)/2ε
=− N 1+ E log 1 1+ E − N 1− E log 1 1− E 2 Nε 2 Nε 2 Nε 2 Nε
と書いておきましょう。すなわち,
S(E,N)=−kN 1 1+ E log 1 1+ E + 1 1− E log 1 1− E ・・・[*] 2 Nε 2 Nε 2 Nε 2 Nε
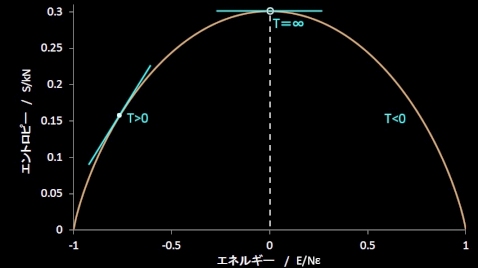
が,2準位系のエントロピーを粒子数,エネルギーの関数として表した式です。系のエントロピーとエネルギーの関係は下図のようになります。途中近似式は用いていますが,SとEは1対1関数であり,Nが大きいため,連続関数として扱います。つまり,ざっくりと微分可能としてしまいます。
また,この関係式は系のミクロな情報 (今の場合,1粒子エネルギーはたった2つのエネルギー状態だけをもつということ) を含んでいることに注目して下さい。熱力学ではこのようなミクロな情報を反映した熱力学変数の関係式を導くことはありませんでした(不可能!)。理想気体の状態方程式も天下り的に与えたものです。
ところが,統計力学では,出発点において分子原子レベルのミクロなモデルに基づいた様々な情報,パラメータをエントロピーに組み入れることができます。そして,それらを含むエントロピーや後に示すような,それ以外の熱力学変数(または関数)とその関係式をも導き出すことが可能となります。その結果,巨視的な熱力学変数の測定からミクロなパラメーターを求めたり,ミクロなモデルの妥当性を検証することが可能となります。今の例では,εというミクロなエネルギー準位(パラメーター)の情報を含んだエントロピー,[*]式が導かれたわけですが,これは熱力学の範囲で議論していては決して得ることのない関係式です。ここのところが統計力学の熱力学に対する優位点なのです。
上図
[5] 以上でこの系に関する統計力学独特の話は実質的に終わりです。物理法則としての番号は付いていませんが,ここに示した2つ原理によって統計力学は演繹的に体系化されていきます。しかし,ここから先の話は統計力学とはいっても,熱力学のパクリでしかありません。熱力学の体系が内部エネルギーから出発していろいろな熱力学関数を導き出していったように,統計力学はエントロピーから出発して,他の”統計力学的”熱力学関数U,G,Fなどを導いていくのです。熱力学の成果を横目で見ながら。
統計力学を熱力学へ対応させながら話を進めるためにはミクロ的な視点とマクロ的な視点との間のギャップを埋める必要があります。その際,数学的な言葉を用いるならば,離散的な変数を連続的な変数とみなすことが必要となります。ボルツマンの原理をもう一度書くと,
S(E,N)=k log W(E,N)
となりますが,右辺の状態数は1,2,・・・と数えることができる離散変数です。ということは,その対数をとった左辺のエントロピーも離散的な変数であるはずです。つまり,統計力学的エントロピーは離散的な量なのです。したがって,統計力学的エントロピーS(E,N)をEで微分することは数学的には許されないはずです。ところが,以下のとおり示すように,Eによる微分を平気で行っていきます。その時の言い訳が,「Nが非常に多きいときはEも連続的に変化(分布)するとみなせる」というものです。この主張はほとんど場合正しいです。しかし,絶対的に成り立つ話ではなく,実際,重要な話題であるボース・アインシュタイン凝縮では成立しません。頭の片隅に置いておいてください。
それから,熱力学における「平衡状態においては変化が起こらない」ということを統計力学的に解釈しなおす必要もあります。連続近似と同じように,Nがたいへん大きな数であることが必要条件ですが,より本質的なところは,実際の観測精度に限界があるために,ある一定値以下の差異は区別できないというところにあります。つまり,有効数字が10桁であるならば,11桁目以降が異なる状態は同一とみなさざるを得ないということです。これはNが大きいとして行われる数学的な近似とは全く別の話ですし,量子論とも関係なく受けれるべきものです。
[1] 微視的状態数とエントロピーとの対応付けが統計力学の出発点にあるといいましたが,系のエントロピーとエネルギー,および,粒子数との関係式 を具体的に定めることができれば,他の様々な熱力学量を導出することはまったく容易です。ここから先の議論は,実質的に熱力学体系の再構築に過ぎないものです。
さっそく,2準位系についてやってみましょう。[*]をEで微分すると,
∂S N =− k log 1 1+ E −log 1 1− E ・・・(5) ∂E 2ε 2 Nε 2 Nε
ここで,熱力学で学んだ公式[#],
∂S N = 1 ・・・(6) ∂U T
を思い出します。Tは言うまでもなく,系の温度です。孤立系のエネルギーEとした量は熱力学の内部エネルギーU=<E>に対応します。
E = <E> (系の平均エネルギー) = U (系の内部ネルギー)
上図(1.の最後)のようにエントロピーのエネルギー依存性に対するプロットの傾きの逆数から温度を算出することができるということです。そこで,(5)と(6)を等価とみなし,
∂S N ≡ 1 ∂E T
これを統計力学的温度の定義とします。(熱力学公式(6)とは全く関係なく,統計力学の体系の中での独自に定義したとの立場もありますが,・・・) (5)と(6)の右辺をイコールとおき,式を整理すると,
2ε =−log 1+E/Nε kT 1−E/Nε
さらに,Eについて解くと,
E=−Nε exp(ε/kT)−exp(-ε/kT) exp(ε/kT)+exp(-ε/kT)
[2] このままでもよいのですが,E→Uと書き改め,双曲正接関数を用いると,
∴ U(T,N)=E(T,N)=−Nεtanh ε ・・・(7) kT
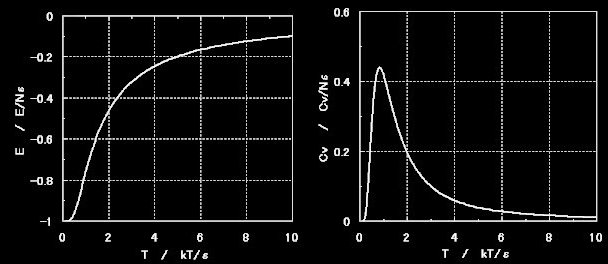
これが2準位系の内部エネルギーを温度の関数として書き表した式です(下図に図示)。
なお,双曲正接関数は,
tanh(x)= exp(x)−exp(-x) exp(x)+exp(-x)
で定義されますが,見慣れてない人のために双曲線関数についてはこちらにまとめました。⇒[#]
[3] (7)のグラフを下に示しました(T>0)が,温度が0Kに近づくと,すべての粒子は低い準位に入り,系全体のエネルギーが(−Nε)にどこまでも近づくのに対し,高温になるにつれ,上側のエネルギー準位にある粒子数が徐々に増えてゆき,T→∞の極限では高低2つの準位に同数の粒子が配分されるようになる(E→0)ことがわかります。さらに(7)を温度Tで微分すると,
∂E =Nk ε 2 sech2 ε ・・・(8) ∂T V,N kT kT
ここでも熱力学の等積比熱の定義式,
Cv≡ ∂U ∂T V
を思い出して,内部エネルギー U ⇔ E と対応させれば,この系の比熱が(8)式で与えられることがわかります。
[4] すなわち,2準位系の比熱は,
Cv=Nk ε 2 sech2 ε [等積比熱] kT kT
この比熱と内部エネルギーの温度依存性のグラフを下に示します。
下図
(問題)
なぜこの系は,ある温度で比熱が最大値をとるかその物理的な意味を説明せよ。
[6] 次にヘルムホルツ自由エネルギーを計算します。まず,[*]式を次のように書き直しておきます。
S(E,N)=−kN 1 log 1 1+ E 1− E + E log
1+ E Nε 2 4 Nε Nε 2Nε
1− E Nε
これを変数Eから変数Tの関数に変換するために(7)式(E⇔U)を代入してEを消去すると,,
S(T,N)=− kN log 1 1−tanh2 ε − kN tanh ε ・ log
1−tanh ε kT 2 4 kT 2 kT
1+tanh ε kT
=−kN 1 log 1 1−tanh2 ε + kN tanh ε ・ log
exp(-ε/kT) 2 4 kT 2 kT
exp(ε/kT)
=Nk log 2cosh ε − Nε tanh ε ・・・(10) kT T kT
したがって,熱力学公式と(7)式を再び用いると,
F ≡U−TS
=-Nεtanh ε −T Nk log 2cosh ε − Nε tanh ε kT kT T kT
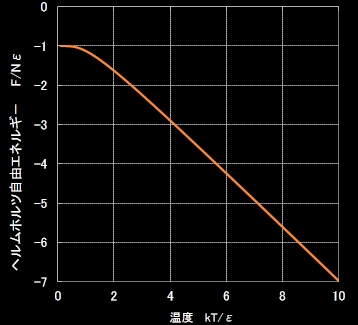
∴ F=−NkT log 2cosh ε kT
[7] まとめるにあたって,もう一度,念を押しておきますが,ここまで,全く新規に導入した物理法則はボルツマンの原理と等重率の原理の2つだけです。これらは証明なしで受け入れる必要のある概念です。しかし,残りの関係式は熱力学においてすでに定義されている物理量のパクリです。下に示した(ヘルムホルツ)自由エネルギーの温度依存性も熱力学安定性から要求される特徴(上に凸な減少関数)を満たしています。めでたし!
[1] ひき続き2準位系を考えていきますが,温度が与えられたとき,2つの準位にいくつの粒子が配分されているか,つまり,分布関数を考えます。それは次の方程式,
(Nε−E)/2ε=N1
(Nε+E)/2ε=N2
E=−Nε exp(ε/kT)−exp(-ε/kT) exp(ε/kT)+exp(-ε/kT)
を連立して解けば求まります。Eを消去して,
N1= Nε−E =Nε 2exp(ε/kT) ・ 1 2ε exp(ε/kT)+exp(-ε/kT) 2ε
= N exp(ε/kT) Z1
ただし,Z1=exp(ε/kT)+exp(-ε/kT)とおきました。
N2も同様に,
と求められます。
N2= N exp(-ε/kT) Z1
これらを図示すると次のとおりです。
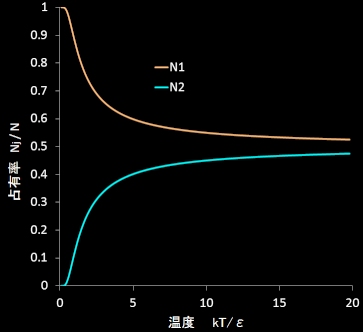
この図からは,温度が低いときは下の準位にある粒子が大多数であるが,温度が上昇するにつれて,それが減少し,その分だけ上の準位のある粒子数が増えてゆき,その差はゼロ,すなわち,N1=N2に近づいていくことがみてとれます。
[2] この問題では2つのエネルギー準位の粒子数(分布)は簡単な計算から求められましたが,エネルギー準位の数が増えてくるなど複雑な系になってくると,簡単に解くことはできなくなります。そこで,普遍性のある解法として最大確率分布を求める方法を示しておきましょう。熱平衡状態ではエントロピーが極大値をとるという熱力学の知見を採用すると,統計力学的エントロピーを与える微視的状態においても極大値をとるはずです。平衡状態においてそのような条件を満たすときの各エネルギー準位にある粒子数を最大確率分布と呼びます。
まず,系のエントロピーを各エネルギー準位にある粒子数N1,N2の関数として書き表すと,
S=klog N! =k(NlogN-N−(N1logN1−N1)−(N2logN2−N2)) ・・・・[**] N1!N2!
となります。このとき,E,N一定の条件下,すなわち,
N1+N2 =N 一定
−εN1+εN2 =E 一定
において,Sを最大とする分布は,ラグランジュの未定係数法[#]を利用して求められます。すなわち,ラグランジュの未定係数をα,βを用いて,
S~=S/k−α(N1+N2)−βε(N2−N1)
を最大とするN1,N2を求めてやればよいのです。その極値は,
∂S~ =−logN1−α+βε=0 ∂N1
∂S~ =−logN2−α−βε=0 ∂N2
から求まります。これより,最大確率分布は,
N*1=exp(−α+βε)
N*2=exp(−α−βε)
となります。
[3] 未定係数α,βが残ったままです。これを定めるためには,N*1,N*2 を[**]に代入して,
S*=k(NlogN−N−(N*1logN*1−N*1)−(N*2logN*2−N*2))
=k(NlogN−N−(N*1(−α+βε)−N*2(−α−βε)+(N*1+N*2))
=k (NlogN+αN+βE)
ここで再び,熱力学のエントロピーと温度との関係式を用いれば,
∂S* N =kβ ⇔ 1 ∂E T
つまり,⇔を=とみなせば,
β= 1 kT
としてよいでしょう。もう一つの未定係数は,
N=N*1+N*2=e-α(eβε+e-βε)
∴ e-α=N/(eβε+e-βε)
=N/Z1
を満足するαとして定まります。ただし,すでに,β=1/kTはわかっており,
Z1≡(eε/kT+e-ε/kT) ← 実は,1粒子分配関数とも呼ぶ
と定まります。
[4] まとめると,
|
2準位系の最大確率分布
Z1≡exp(ε/kT)+exp(-ε/kT) |
||||||||||||||
これは,初めに[1]で連立方程式を直接解いた結果とまったく同じです。
このページで行ったような,1.等重率の原理,2.ボルツマンの原理からエントロピーを定義し,そこから熱力学関係式を参考にしながら,統計力学を定式化していく方法をミクロカノニカルアンサンブル(小正準集団)の方法と言います。その一般的な手順を体積を変数に含めてフローチャートにすると次のようになります。
P(E,V,N)=T ∂S ∂V E,N ↑ W(E,V,N)
[等重率]⇒ S(E,V,N)=klogW
↓↑
E=U(S,V,N)
自然な変数→
1 = ∂S T(E,V,N) ∂E V,N ↓ ↓E について解いて
μ(E,V,N)=−T ∂S ∂N E,V E(T,V,N)⇔U(T,V,N) →
Cv= ∂U ∂T V,N ↓F=U−TS F(T,V,N)
自然な変数→
P(T,V,N)=− ∂F ∂V T,N
→ はここで示した変形
SUSTAINABLE TOKIWADAIGAK SINCE 2002
公式
log n!= n log n − n
余弦/正割
偶関数
cosh x = ex+e-x 2
sech x = 2 = 1 ex+e-x cosh x 正弦/余割
奇関数
sinh x = ex−e-x 2
csch x = 2 = 1 ex−e-x sinh x 正接/余接
奇関数
tanh x = ex−e-x ex+e-x
coth x = ex+e-x = 1 ex−e-x tanh x
tanh x = sinh x cosh x
公式
1−tanh x =2e-x/(ex+e-x), 1+tanh x =2ex/(ex+e-x)
二乗の関係
cosh2x−sinh2x = 1
1−tanh2x= 1 =sech2x cosh2x
coth2x−1= 1 =csch2x sinh2x
微分
d cosh x=sinh x dx
d sech x=− sinh x =−sech x tanh x dx cosh2x
d sinh x=cosh x dx
d csch x=− cosh x =−csch x coth x dx sinh2x
d tanh x= 1 =sech2x dx cosh2x
d coth x=− 1 =−csch2x dx sinh2x
熱力学公式 dE =TdS−PdV+μdn [#]から得られる,
μ(E,V,N)=−T ∂S ∂N E,V
を用いて化学ポテンシャルを計算します。2準位系のエントロピーを再掲すると,
S(E,N)=−kN { 1 1+ E log 1 1+ E + 1 1− E log 1 1− E } ・・・[*] 2 Nε 2 Nε 2 Nε 2 Nε
これををNで微分すると,
∂S =−k { ・・・ } −kN 1 −E log 1 1+ E + 1 E log 1 1− E ∂N E,V 2 N2ε 2 Nε 2 Nε 2 Nε
+ 1 1+ E
(−E/N2ε) + 1 1− E
E/N2ε 2 Nε
1+ E Nε 2 Nε
1− E Nε
=−k 1 log 1 1+ E + 1 log 1 1− E 2 2 Nε 2 2 Nε
=− k log 1 1− E 2 2 4 Nε
↓ (7)よりE(=U)を消去
=− k log 1 1−tanh2 ε 2 4 kT
=− k log 1 2 4cosh2(ε/kT)
=k log 2cosh ε kT
よって,
μ(E,V,N)=−T ∂S =−kT log 2cosh ε ∂N E,V kT