| 15 積分変数の変換 | ||
| f-denshi.com [目次] 最終更新日:03/05/05 | ||
| サイト検索 | ||
[1] 2変数の場合の積分変数変換の一般論を示します。(次元の拡張は形式的にできます。)
C1級の関数,x=x(u,v),y=y(u,v) を用いた変数変換:
Φ : (u,v) ⇒ (x,y)≡(x(u,v),y(u,v)) ; (x,y),(u,v) ∈ R2
Φ-1 : (x,y) ⇒ (u,v)≡(u(x,y),v(x,y))
つまり,
(x,y)=Φ(u,v)=(x(u,v),y(u,v))
とその逆関数を考えます。
| 定理 [積分変数変換] (1) Φを正則な C1-写像とする。U を面積確定な有界領域とすると, Φ(U) も面積確定な有界領域で, dxdy =|J(xy/uv)|dudv および, ただし, |J(xy/uv)|=ヤコビの行列式 J(xy/uv) の絶対値, (2) 3変数の場合は, dxdydz=|J(xyz/uvw)|dudvdw
|
[証明] ちょっとたいへんなので略。 どうしてもという人は ⇒ [#]
[2] 以下,考え方だけ
ヤコビアンの導入[#]に用いる式,
Δx = xu xv Δu Δy yu yv Δv
をよくみると,変数変換の前後で微小な線分(微分要素)が線形写像で関係づけられています。したがって,変数変換の前後での面積の関係もここから得られるはずです。(つまり,極所的に C1写像は線形写像で近似できるハズ!)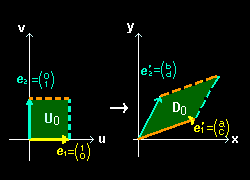
そこで,一般に行列Aによる線形写像によって面積がどのように変わるのか調べてみます。右図のように,u-v (直交)座標系の単位ベクトル,
e1= 1 , e2= 0 0 1
とします。この基底ベクトルの張る領域 U0 の面積は1です。
| [3] 一方,正則な行列[#], | A= | a b | で表せる線形写像によって,e1,e2 は, | ||
| c d |
e1'= a b 1 = a c d 0 c
e2'= a b 0 = b c d 1 d
に移ります。これに対応して領域 U0 は,e1',e2' の張る平行四辺形である領域 D0 に移ります。ところで,e1'e2' の張る平行四辺形 D0 の面積は,これらのベクトルの外積の絶対値であり,行列 A の行列式の絶対値に等しくもあります。すなわち,
[ D0 の面積 ]=|e1'×e2'|=|ad−bc|=|detA|・[ U0の面積=1 ]
ここで,極小さな領域では,
a b = xu xv c d yu yv
と近似できる[#]ことを思い出すと,
dxdy =|detA|dudv =|J(xy/uv)|dudv
と表しても良いだろうと推測できます。これらは n 変数についてそのまま拡張できます。ちなみに,n=3 のときは正方形の代わりに領域 U0 を立方体,領域 D0 を平行6面体[#]として同じような考察ができます。
(幾何学的な直感が働くのは3次元までですが,4次元以上へ拡張も形式的な拡張が可能です。)
[1] 2次元直交座標−極座標
Φ: (r,θ) ⇒ (X,Y)
定理で,次の置き換え,
x → X
y → Y
u → r
v → θ
x=x(u,v) → X(r,θ)=r cosθ
y=y(u,v) → Y(r,θ)=r sinθ
とするとヤコビアンの絶対値は,
| |J(XY/rθ)|= |
|
|
= | cosθ | -r sinθ | = r | |||||||||||||
|
|
sinθ | r cosθ |
よって,
dXdY = r ・drdθ ← 定理: dxdy=|J(xy/uv)|dudvより
[2] 3次元直交座標−球座標
Ψ: (r,θ,φ) ⇒ (X,Y,Z)
置き換え,
x → X
y → Y
z → Z
u → r
v → θ
w → φ
によって
x=x(u,v,w) → X(r,θ,φ)=r sinθ cosφ
y=y(u,v,w) → Y(r,θ,φ)=r sinθ sinφ
z=z(u,v,w) → Z(r,θ,φ)=r cosθ
|J(XYZ/r,θ,φ)|=
∂X ∂r
∂X ∂θ
∂X ∂φ
∂Y ∂r
∂Y ∂θ
∂Y ∂φ
∂Z ∂r
∂Z ∂θ
∂Z ∂φ
= sinθcosφ rcosθcosφ -rsinθsinφ sinθsinφ rcosθsinφ rsinθcosφ cosθ -r sinθ 0
= r2sinθ
(行列式の計算は→こちら[#]を参照してご自分で。)
0≦θ≦π ⇒ sinθ≧0 です。
座標変換については,「ベクトル解析」 5.直交曲線座標 [#] も参照してください