２　 行列式の定義にどうやってたどり着くのか
f-denshi.com  最終更新日：06/03/17

「はじめての線形代数」PDF版がこちらからダウンロードできます。
         ⇒       　無料見本　

ここでの予備知識は高校生で習う３次元までのベクトル2次の行列式くらいまでとして，n元連立１次方程式の一般解の公式を予想して見ましょう。

高校数学の復習からです。未知数，x₁，x₂ についての連立１次方程式です。その一般式は，

a₁₁x₁＋a₁₂x₂＝b₁
a₂₁x₁＋a₂₂x₂＝b₂

となります。これを，x₂ を消去するために，

   a₂₂a₁₁x₁＋a₂₂a₁₂x₂＝ a₂₂b₁
−a₁₂a₂₁x₁−a₁₂a₂₂x₂ ＝−a₁₂b₂

と変形して，辺々たせば，

( a₂₂a₁₁−a₁₂a₂₁ )x₁ ＝　a₂₂b₁−a₁₂b₂

したがって，a₂₂a₁₁−a₁₂a₂₁≠0　であるならば，

∴　x1＝	a22b1−a12b2
	a22a11−a12a21

と解の半分が求まります。次に，x₁ を消去して，x₂ を求めるために与式を

−a₂₁a₁₁x₁−a₂₁a₁₂x₂＝−a₂₁b₁
   a₁₁a₂₁x₁＋a₁₁a₂₂x₂＝ a₁₁b₂

として，辺々を足せば，

( a₁₁a₂₂−a₂₁a₁₂ )x₂＝−a₂₁b₁＋a₁₁b₂ 

したがって，a₁₁a₂₂−a₂₁a₁₂≠0　であるならば，

∴　x2＝	−a21b1＋a11b2
	a11a22−a12a21

ともう片方の解 x₂ も求まります。

ここで，解　x₁，x₂の分母はよく見ると同じであって，連立一次方程式を行列とベクトルを用いて，

a11 a12 x1 ＝ b1 a21 a22 x2 b2

と表したときの連立一次方程式の係数からなる行列の行列式であって，

A ＝		a11 a12		とすると，　|A|　＝		a11	a12		＝ a11a22−a12a21
		a21 a22				a21	a22

と定義されものです。なお，|A| は det A とも書きます。

連立方程式を解く途中で仮定した，a₂₂a₁₁−a₁₂a₂₁≠0　という条件は，行列 A が逆行列を持つ条件で，この条件が成り立つならば，式に左から逆行列 A^-1 をかけて，

x1

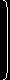＝ A-1

b1

＝

1 |A|

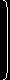a22

−a12

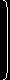b1

＝

a22b1−a12b2 |A|

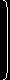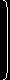x2

b2

−a21

a11

b2

−a21b1＋a11b2 |A|

が連立１次方程式の解となります。以上が高校生の時にも習ったことの復習です。

  さて，大学レベルになると未知数が任意のnである場合の連立一次方程式を習うこととなりますが，今示した解法を眺めていただけではさすがにその一般解を予想することは不可能なので，もうひとつ次元を増やして３元連立方程式を調べてみます。解くべき連立一次方程式を，

a11x1＋a12x2＋a13x3＝b1 a21x1＋a22x2＋a23x3＝b2 a31x1＋a32x2＋a33x3＝b3

とします。計算の見通しをよくするために未知数として， x，y，z　ではなくで，x₁，x₂，x₃　と番号を用いてます。まず，x₃ を消去するために，

a23a11x1＋a23a12x2＋a23a13x3	＝	a23b1	(1)’
a33a11x1＋a33a12x2＋a33a13x3	＝	a33b1	(1)”
−a13a21x1−a13a22x2−a13a23x3	＝	−a13b2	(2)’
−a13a31x1−a13a32x2−a13a33x3	＝	−a13b3	(3)’

と変形して，(1)’＋(2)’，および，(1)”＋(3)’ から，

(a₂₃a₁₁−a₁₃a₂₁)x₁＋(a₂₃a₁₂−a₁₃a₂₂)x₂＝a₂₃b₁−a₁₃b₂
(a₃₃a₁₁−a₁₃a₃₁)x₁＋(a₃₃a₁₂−a₁₃a₃₂)x₂＝a₃₃b₁−a₁₃b₃

今度は x₂ を消去するために，

辺々足して，

{(a₃₃a₁₂−a₁₃a₃₂)(a₂₃a₁₁−a₁₃a₂₁)−(a₂₃a₁₂−a₁₃a₂₂)(a₃₃a₁₁−a₁₃a₃₁)}x₁

　　　　　　　　＝(a₂₂a₃₃−a₃₂a₂₃)a₁₃b₁−(a₃₃a₁₂−a₁₃a₃₂)a₁₃b₂＋(a₂₃a₁₂−a₁₃a₂₂)a₁₃b₃

さらに，両辺 a₁₃ で除して，整理すると

{{a₁₁(a₂₂a₃₃−a₂₃a₃₂)−a₁₂(a₂₁a₃₃−a₂₃a₃₁)＋a₁₃(a₂₁a₃₂−a₂₂a₃₁)}}x₁

　　　　　　　　＝(a₂₂a₃₃−a₃₂a₂₃)b₁−(a₁₂a₃₃−a₃₂a₁₃)b₂＋(a₂₃a₁₂−a₁₃a₂₂)b₃

ここで，

左辺  ＝

a11

a22

a23

−a12

a21

a23

＋a13

a21

a22

x1

a32

a33

a31

a33

a31

a32

右辺　 ＝

a22

a23

b1−

a12

a13

b2＋

a12

a13

b3

a32

a33

a32

a33

a22

a23

と２次の行列式を用いてまとめられます。ところで，この行列式たちをよく見ると，連立１次方程式を行列で表した，

a11 a12 a13 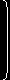x1 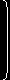＝ b1 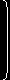a21 a22 a23 x2 b2 a31 a32 a33 x3 b3

の行列 ( a_ij) から作られる３行３列の行列式において，下に灰色で示したような行と列を取り除いて作られる２行２列の行列式となっていることがわかります。すなわち，左辺の方は，

		a11	a12	a13		⇒	a22 a23 a32 a33	≡ ▲11
		a21	a22	a23
		a31	a32	a33

		a11	a12	a13		⇒	a21 a23 a31 a33	≡ ▲12
		a21	a22	a23
		a31	a32	a33

		a11	a12	a13		⇒	a21 a22 a31 a32	≡ ▲13
		a21	a22	a23
		a31	a32	a33

および 右辺の方は，

		a11	a12	a13		⇒	a22 a23 a32 a33	≡ ▲11
		a21	a22	a23
		a31	a32	a33

		a11	a12	a13		⇒	a12 a13 a32 a33	≡ ▲21
		a21	a22	a23
		a31	a32	a33

		a11	a12	a13		⇒	a12 a13 a22 a23	≡ ▲31
		a21	a22	a23
		a31	a32	a33

すると，

左辺＝( a₁₁▲₁₁−a₁₂▲₁₂＋a₁₃▲₁₃ ) x₁

右辺＝b ₁▲₁₁−b₂▲₂₁＋b₃▲₃₁

となります。このままでもいいのですが，２項目についているマイナスの符号を統一的に記述するために，

Δ_jk＝(-1)^j+k ▲_jk

とさらに書き直しておきます。　すると，連立方程式の解，x₁ は，

x1 ＝	b1Δ11＋b2Δ21＋b3Δ31	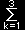＝	bkΔk1
	a11Δ11＋a12Δ12＋a13Δ13		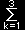a1kΔ1k

となります。添え字が対称的であることから，x₂，x₃ については，

x2 ＝	b1Δ12＋b2Δ22＋b3Δ32	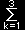＝	bkΔk2
	a21Δ21＋a22Δ22＋a23Δ23		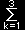a2kΔ2k

x3 ＝	b1Δ13＋b2Δ23＋b3Δ33	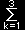＝	bkΔk3
	a31Δ31＋a32Δ32＋a33Δ33		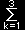a3kΔ3k

となります。ここで，導入した Δ_mn なる行列式は頻繁に現れるので名前がついており，行列の(m,n)-余因子と呼ばれています。
また，分母は未知数ごとに３とおり，すなわち，

a1kΔ1k

a2kΔ2k

a3kΔ3k

と表されていますが，ベタ書きしてみれば，これはすべておなじで，

a₁₁a₂₂a₃₃−a₁₁a₂₃a₃₂＋a₁₂a₂₃a₃₁−a₁₂a₂₁a₃₃＋a₁₃a₂₁a₃₂−a₁₃a₂₂a₃₁

という６つの項の和です。これは，２元連立１次方程式の解の分母が行列式 |A| となっていることを思い出せば，３次の行列式の定義としてふさわしいものに違いありません。そこで，３次の行列式を，

|A’|＝a₁₁a₂₂a₃₃−a₁₁a₂₃a₃₂＋a₁₂a₂₃a₃₁−a₁₂a₂₁a₃₃＋a₁₃a₂₁a₃₂−a₁₃a₂₂a₃₁　　・・・・・・　[*]

と定義します。ここで，

A’ ＝		a11 a12 a13
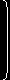		a21 a22 a23
		a31 a32 a33

です。

一方，２元連立１次方程式の一般解の分子を見てみると，２次の行列の場合の余因子は，

a₂₂＝Δ₁₁，　-a₁₂＝Δ₂₁，　-a₂₁＝Δ₁₂，  a₁₁＝Δ₂₂

と書くことができるので，

２元連立１次方程式の解の公式
x1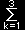＝ bkΔk1 |A|	x2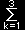＝ bkΔk2 |A|
３元連立１次方程式の解の公式
x1 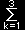＝ bkΔk1 |A’|	x2 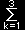＝ bkΔk2 |A’|	x3 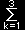＝ bkΔk3 |A’|

このように並べて書いて見れば，n元連立１次方程式の解がどうあるべきか見えてきますね。

ところで，３次の行列式は間に合わせ的に[*]のように定義しましたが，n次行列の行列式について考えるにはもう少し深く掘り下げておく必要があります。

　３次の行列式に現れる６つの項を注意深く見ると，すべて，a_1pa_2qa_3r　という形をしていて，p，q，r の組は，

( p,q,r )＝(1,2,3)，(1,3,2)，(2,3,1)，(2,1,3)，(3,1,2)，(3,2,1)

となっています。これは３文字(123)の順列のすべてを尽くしていて，その個数，3！＝6　から構成されていることに気づきます。このような見方は２次の行列式についても当てはまって，そこに現れる項は，a_1pa_2q ，(pq)＝(1，2)，(2，1) という形をしています。たいぶ，n次の行列式の定義がどうあるべきか見えてきましたね。あと，マイナス符号についてははちょっと頭をひねる必要がありますが，それは (1,2,3) から出発して，３文字のうち２文字だけその順序を交換していくと，

(1,2,3)	⇒ 2と3交換	(1,3,2)	⇒ 3と1交換	(3,1,2)	⇒ 1と2交換	(3,2,1)	⇒ 2と3交換	(2,3,1)	⇒ 3と1交換	(2,1,3)	⇒ 1と2交換	(1,2,3)
(+)		(-)		(+)		(-)		(+)		(-)		(+)

という循環する系列が得られます。そして，順列の一つ一つには下に記したような符号を一意的に対応させられそうです。２次の場合に戻って考えても，

(1,2)	⇒ 1と2交換	(2,1)	⇒ 2と1交換	(1,2)
(+)		(-)		(+)

となって同じ規則で符号が付けられそうです。そして，この規則を用いれば任意のn次の行列式をどのように定義すればよいか見通しが得られました。そこでは，置換という考え方が重要になってくるのです。

［目次へ］

ちょっと小言

数学で直感は大事です。特に幾何学的なイメージに直して図解することはたいへん理解の助けになります。しかし，あまりこれを強調しすぎるのもどうかと思うことも多いのも事実。このページのように行列を成分で書いてこつこつ計算することが欠かせないような状況もあることは強調しておいてもよいのではないでしょうか。一般化による抽象的な表記法も場合によっては重要であり，本質的な役割を果たします。ここでは，連立一次方程式を，

a11x1＋a12x2＋a13x3＝b1 a21x1＋a22x2＋a23x3＝b2 a31x1＋a32x2＋a33x3＝b3

と書いたからこそ本文中で述べた規則性を見出し，高次の行列式にたどり着けたのであって，もし，

ax＋bY＋cZ＝d ex＋fY＋gZ＝h px＋qY＋rZ＝s

と書いたなら，行列式の定義はまず，頭の中にひらめかないでしょう？

|A|＝afr−agq＋bgp−ber＋ceq−cfp　

をそのまま観ていてもただの暗号にしか見えない！