 |
1 行列の定義と略記法 |
|
| f-denshi.com 最終更新日:03/06/23 |
「はじめての線形代数」PDF版がこちらからダウンロードできます。
⇒ 無料見本
高校生で習う程度の行列 (matrix) の知識を前提に行列の定義と基本的な用語についてまとめておきます。必ずしもここでは厳密な言い方をしていませんが,連立1次方程式
(simultaneous linear equations)論を理解するには十分でしょう。
1.表記法
[1] m行n列の行列A,Bの表記はスペース等の都合によっていろいろ使い分けをします。よく使われる方法を列挙します。成分
(element) を書き並べるもっとも標準的な表し方は,
| A = |
 |
a11 a12 ・・・・ a1n |
 |
B = |
 |
b11 b12 ・・・・ b1n |
 |
| a21 a22 ・・・・ a2n |
b21 b 22・・・・ b2n |
| : : ・・・・ : |
: : ・・・・ : |
| am1 am2 ・・・・ amn |
bm1 bm2 ・・・・ bmn |
と書きますが,これはスペースをとるのでしばしば節約のために,
B = (bmn)
などと書きます。ここで成分(要素ともいう) amn,bmn は実数,または複素数です。
[2] 列数が1の行列
 |
b11 |
 |
| b21 |
| : |
| bm1 |
を列ベクトル (column vector),行数が1の行列
(a11a12・・・・a1n)
を行ベクトル (row vector) と呼ぶことにしましょう。この用語を用いると,中ぐらい略した表現として,行列の各列を列ベクトルとしてまとめて扱った,
| B ≡ |
 |
b11 b12 ・・・・ b1n |
 |
≡ (b1,b2,・・・,bn); |
| b21 b 22・・・・ b2n |
| : : ・・・・ |
| bm1 bm2 ・・・・ bmn |
| ただし,b1= |
 |
b11 |
 |
,b2= |
 |
b12 |
 |
,・・・・ |
,b2= |
 |
b1n |
 |
| b21 |
b22 |
b2n |
| : |
: |
: |
| bm1 |
bm2 |
bmn |
のような書き方ができます。場合によっては,各行を行ベクトルとしてまとめて,
| A= |
 |
a1 |
 |
| a2 |
| : |
| an |
ただし,a1=(a11a12・・・a1n),a2=(a21a22・・・a2n), ・・・,an=(an1an2・・・ann)
とも書くことにしましょう。
[3] 行列A,Bの積 (product) は,AB と書きますが,積の定義が可能なのはAの列数とBの行数が等しいときだけで,
m行k列の行列A とk行n列の行列Bの積は,
| AB= |
 |
a11 a12 ・・・・ a1k |
 |
| ・・・・・・・・・・・・ |
| am1 am2 ・・・・ amk |
|
 |
b11 ・・ b1n |
 |
| ・・・・・・ |
| ・・・・・・ |
| bk1 ・・ bkn |
|
| = |
 |
a11b11+・・・+a1kbk1 |
・・・ |
a11b1n+・・・+a1kbkn |
 |
| : |
・・・ |
: |
| : |
・・・ |
: |
| am1b11+・・・+amkbk1 |
・・・ |
am1b1n+・・・+amkbkn |
|
と定義され,m行n列の行列となります。これが,
| C = |
 |
c11c12・・・・c1n |
 |
| : ・・・・・ : |
| cm1cm2・・・・cmn |
|
に等しい,すなわち,C=AB とすると,C の s行 t列成分 cst は,
| cst = |
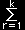 |
asrbrt |
|
と書くことができます。また,ベクトルを用いた行列の表現方法を使うと,
AB =A(b1,b2,・・・,bn)
| = |
 |
a1 |
 |
(b1,b2,・・・,bn)= |
 |
a1b1 ・・・・・ a1bn |
 |
| a2 |
a2b1 ・・・・・ a2bn |
| : |
: |
| am |
amb1 ・・・・・ ambn |
などとも書くことができます。ここで,asbt は,
| asbt=(as1as2・・・・ask) |
 |
b1t |
 |
| = |
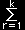 |
asrbrt = cst |
|
| b2t |
| : |
| bkt |
であり,行列成分が実数ならば,as と bt の内積as・bt (inner product , scalar product ) と同じになります。
2 用語
行列要素の並び方に特徴のある行列には呼び名が付いてます。これを整理しておきましょう。
[1] 正方行列 A
行と列の数が等しい行列,
| |
 |
a11 ・・・ a1n |
 |
| A=(ann)= |
: ・・・ : |
| |
an1 ・・・ ann |
をn次の正方行列 (square matrix) といいます。応用上この形をした行列はもっとも重要です。
| 行列Aに対して,各成分を共役複素数[#]に置き換えた行列 [ ast → |
|
|
] |
| ast |
|
|
= |
|
|
|
|
|
| |
 |
a11 |
・・・ |
a1n |
 |
| A |
: |
・・・ |
: |
|
|
|
|
| |
an1 |
・・・ |
ann |
| を共役行列 (conjugate matrix)といいます。行列要素が実数の時は |
|
[3] 転置行列 tA
行列Aに対して,その行と列を入れ換えた行列[ ast→ ats ]
| |
 |
a11 |
・・・ |
an1 |
 |
| tA= |
・・ |
・・・ |
・・ |
| |
a1n |
・・・ |
ann |
を転置行列 (transpose matrix )といい,tAと書きます。
[4] 随伴行列 A*
| 行列Aに対して,行と列を入れ換えると同時に各要素を共役複素数に置き換えた行列[ ast → |
|
] |
| ats |
| A*= |
|
|
|
|
|
 |
a11 |
・・・ |
an1 |
 |
|
|
|
| : |
・・・ |
: |
|
|
|
| a1n |
・・・ |
ann |
を
随伴行列 (adjoint matrix ) といい
A*と書きます。また,成分がすべて実数ならば,
A*=
tA に注意して下さい。随伴行列についての基本的な性質をまとめておきます。
|
随伴行列の基本的な性質 (A,Bは正方行列で,c は複素数)
| (1) (A*)* = A |
|
|
| (3) (AB)* = B*A* |
| (4) (A+B)*= A*+B* |
|
|
| (6) (A*)-1=(A-1)* 逆行列に関して |
|
[5] 三角行列と対角行列 (diagonal matrix )
行と列の番号が等しい対角成分より右上,もしくは左下がすべて0である次のような行列を三角行列といいます。
行列要素は,*の部分では任意の数,O の部分ではすべて0 が並びます。
さらに対角成分,akk 以外の成分がすべて0である行列:
| D= |
 |
α |
0 |
・・・・ |
0 |
 |
| 0 |
β |
0・・ |
0 |
|
・・・・ |
|
| 0 |
・・・・・0 |
ω |
と表します。もちろん,
| 零行列:O= |
 |
0・・・・・0 |
 |
, 単位行列:E=
(unit matrix) |
 |
1 |
0 |
・・ |
0 |
 |
| 0・・・・・0 |
0 |
1 |
・・ |
・・ |
| : |
・・ |
・・ |
1 |
0 |
| 0・・・・・0 |
0 |
・・ |
0 |
1 |
と呼ばれる行列も対角行列の一種です。( ”ベキ零行列” というのもありますが,”すべての成分が0である零行列”とは別物です。→[#] )
ここまでを表にすると下のようになります。
| 名称 |
正方行列 |
|
転置行列 tA |
随伴行列 A*
(共役転置行列) |
| 行列 |
| A= |
 |
a11・・・a1n |
 |
| : ・・・ : |
| an1・・・ann |
|
|
= |
|
|
|
|
|
| |
 |
a11 |
・・・ |
a1n |
 |
|
|
|
|
| A |
: |
・・・ |
: |
|
|
|
|
| |
an1 |
・・・ |
ann |
|
| |
 |
a11 |
・・・ |
an1 |
 |
| tA= |
・・ |
・・・ |
・・ |
| |
a1n |
・・・ |
ann |
|
| A*= |
|
|
|
|
|
 |
a11 |
・・・ |
an1 |
 |
|
|
|
| : |
・・・ |
: |
|
|
|
| a1n |
・・・ |
ann |
|
| 成分 |
ast |
|
[ ast→ ats ] |
|
[5−2] なお,行列Aとその随伴行列A* との間に次のような関係が存在するとき,
| 行列要素が実数のとき |
行列要素が複素数 |
| 名称 |
特徴 |
名称 |
特徴 |
| 対称行列 |
tA=A |
エルミート行列 |
A*=A |
| 交代行列 |
tA=-A |
歪エルミート行列 |
A*=-A |
という名前がついています。対称行列,エルミート行列は固有値理論において主役を演じる行列なので,「固有値論入門」で詳細[#]に説明します。
次に行列の演算が関与する場合について述べます。
[6]逆行列:
n次正方行列Aについて,
AB = BA = E (単位行列)
なる行列 B をA の逆行列 (inverse matrix )といい,B =A-1 とふつう書きます。 成分では,
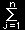 |
asjbjt |
=δst |
と書くことができます。 ここで,δst はクロネッカーのデルタ (Kronecker delta) といい,
| δst= |
 |
1 s=t |
|
| 0 s≠t |
と定義されます。
[7] 直交行列
n次正方行列U を列ベクトルukを並べて,U=(u1,u2,・・・un)と記述したときに,次の関係(内積[#]),
us・ut=tusut=δst
を満たすならば,U を直交行列 (orthogonal matrix) といいます。このとき,U の逆行列がその転置行列tU であることは,
| tUU = |
 |
tu1 |
 |
(u1,u2,・・,un)= |
 |
tu1u1 ・・・tu1un |
 |
= |
 |
1 |
0 |
・・ |
0 |
 |
=E |
| tu2 |
tu2u1 ・・・tu2un |
0 |
1 |
・・ |
・・ |
| : |
: |
・・ |
・・ |
1 |
0 |
| tun |
tunu1 ・・・tunun |
0 |
・・ |
0 |
1 |
と書けばすぐにわかります。直交行列は行列成分が実数の場合の呼び方ですが,複素数も含めて考えるときはユニタリ行列と呼ばれます。
これで最後です。行列T とその随伴行列T* との間に,
が成り立つとき,T を正規行列といいます。これは固有値論[#]の中で詳しく説明します。
[ 目次へ ]