１次元の結晶モデル
f-denshi.com  更新日：

量子力学　103　の続き (の一つ) です。１次元に広がる自由粒子を１次元結晶中の電子とみなす考え方です。

１．LCAO近似　

［１］ 単一原子，N個が等間隔 a で並んだ１次元結晶を周期境界条件のもとで考えましょう。結晶中の電子の波動関数(＝結晶軌道 )　ψ(x) を N個の原子軌道 χ_j(x) の線形結合，

ψ(x)＝

cnχn(x)

で近似することにします。もちろん，ψ(x)はブロッホ関数 [#]となる必要がありますが，n 番目の原子の位置が，

x＝n a　

で表せることに注意すれば，c_n ＝ exp(i kna )　とすればこれを満足します。　ここで，

k＝2πp/(Na)

で，p は整数です。

ψk(x)＝ exp(i kna )χn(x)

［２］　ここで，各原子軌道 χ_n(x) は規格化されており，異なる原子間の原子軌道の重なりが無視できる，すなわち，

χ*n(x) χn(x)dx＝1

χ*m(x) χn(x)dx＝0，　　m≠n

と条件もつけておきましょう。 また，原子軌道に関するエネルギー積分と呼ばれる次の量を α，β とおきます[#]。

χ*n(x) Hχn(x)dx＝α

χ*m(x) Hχn(x)dx＝β，　　n ＝m±1

これらを用いて，摂動論を使って計算した [#] 第１次近似における１次元結晶軌道のエネルギーは，

ψk*(x)ψk(x)dx＝N

および，

ψk*(x)Hψk(x)dx＝

exp(-i kma )χ*m(x) H exp(i kna)χn(x)dx

＝

exp(i k(n−m)a)

χ*m(x) H χn(x)dx

＝ N(α＋βexp(i ka)＋βexp(-i ka))

なので，

E(k)＝ ψk*(x)Hψk(x)dx ＝α＋2βcoska　　　　　　・・・・・・　(1) ψk*(x)ψk(x)dx

詳しくは摂動論 [#] を参考にしてください。

［３］　さて，今求めたE(k)がどのような形をしているのか典型的な２つの具体例で見てみましょう。

波動関数 ψ(x) の周期性(＝波長)が ∞ の場合，つまり，k＝0 であるとき，

(１)　もし，χ_j(x)が  s 軌道ならば，　　⇒ 隣接原子どうしは結合性，つまりβ＜0　
(２)　もし，χ_j(x)が  p-σ軌道ならば，⇒ 隣接原子どうしは反結合性，つまりβ＞0　

であることに注意してE (k) をそれぞれ図示すると左下のようになります。

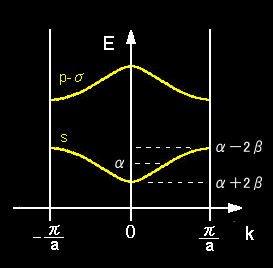	単一原子の１次元鎖  (p-σ)
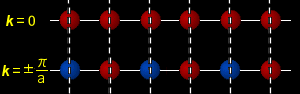
	単一原子の１次元鎖  (s)

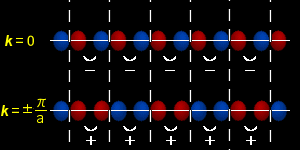
k＝0， および，k＝ ±π/a のときの原子軌道の配列をその右に示しています。

この場合，ともにエネルギーバンド幅は4βであり，

バンド幅は隣り合う原子軌道どうしの相互作用 [#] が強いほど広くなる。

ことがわかります。

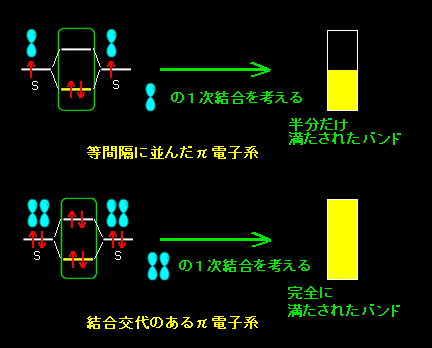
［４］　下にはエネルギーバンドを表す代表的な図を比較して示しました。

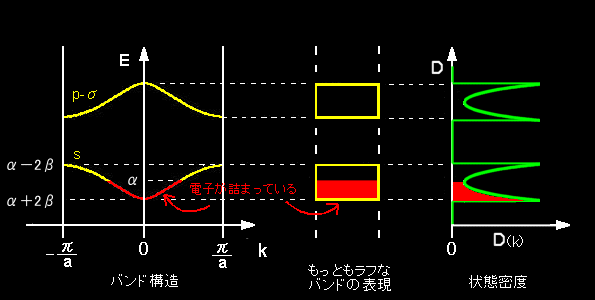
［５］　もう一つの例として，２種類の原子が存在するためイオン性のある(＝分極した)１次結晶，すなわち，

正電荷を帯びた A 原子：　S軌道
負電荷を帯びた B 原子：　P軌道

でバンドを形成している場合の結晶軌道を考えます。

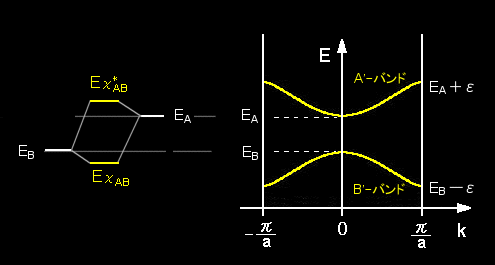
この場合は，まず，原子Aと原子Bの２原子からなる分子軌道を考えて，その結合性軌道χ_AB，反結合性軌道χ^*_AB のそれぞれについて，LCAO-近似を用いた結晶軌道を考えることになります。

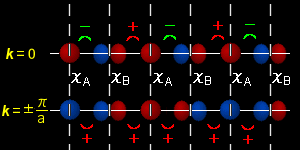
	２種類の原子でできた１次元鎖

k＝0　のとき，　エネルギー　→　最低
k＝±π/a のとき，エネルギー　→最高

［目次］

もし，１種類の１次元原子配列からなるバンドを考える場合でも，結合距離がすべて同じでなく交互に長短が現れる場合もある
⇒　パイエルスの歪