| t122 1次元イジングモデルの繰り込み | |
| f-densHi.com 更新日: 18/04/13 | |
| サイト検索 | |
| 目次へ | |
[1] 繰り込み変換とは,スケール変換によって,系を粗視化,平均化することであって,統計力学ではスケーリン理論として臨界現象などの解析にしばしば用いられます。この変換は続けて繰り返し行うことで(合成写像を算法として閉じている!)その極限に至る過程を考察することから繰り込み群(正確には逆元を考えない,半群と見るべきだが,・・・)とも呼ばれます。ここでは,この技法を1Dイジングモデルを例に見ていきましょう。(結果そのものはつまらないのですがその技法を学びましょう。)
磁場が0の下で,1次元イジングモデルのハミルトニアンを
H=-J σiσi+1
とします。K=βJ とおき,この系の分配関数は,
Z=
Σ Σ ・・・ σ0=±1 σ1=±1 exp(−βH)
=
Σ Σ ・・・ σ0=±1 σ1=±1 exp Kσiσi+1
となります。ここで,すべてのスピン変数に関する和(トレース和)を完全に実行すれば,熱平衡状態,すなわち,完全に平均化された状態を記述する分配関数となるわけですが,繰り込み群の方法では,その一部だけを逐次実行して,その挙動を調べることが行われます。
[2] 具体的な一つのプロセスを示すと,上式中での i が偶数のスピン変数だけを用いて,同じ分配関数を
Z =
Σ Σ ・・・ σ~0=±1 σ~1=±1 A~・exp K~σ~Iσ~I+1
ただし,
σ~I=σ2I
と表すことが行われます。これはスピン演算子の部分が変換前と同形ではあるが,2倍に粗視化されたハミルトニアンから分配関数を計算する(できる)仕方になっています。ここで,A~,及び,K~ は粗視化の前後で分配関数,すなわち,熱力学諸関数が不変となるように定めてやる必要があります。(1次元の場合これが厳密にできる!)
数学的には 奇数の i に対する和だけをあらかじめ実行することになりますが,一つ目のσ1に関しては,(σ3,σ5,・・・を考えても同じ)その関係する部分だけ抜き出すと,
Σ exp[K(σ0σ1+σ1σ2)]= σ1=±1 A~・exp K~σ~0σ~1 =A~・exp K~σ0σ2
を満たす必要がありますが,具体的に数値を入れてみて,
(σ0,σ2)=(1,1),および,(-1,-1)のときは,
e2K+e-2K=A~ exp[K~]
(σ0,σ2)=(1,-1),および,(-1,1)のときは,
1 + 1 = A~ exp[-K~]
が成り立っていなければならないことが分かります。κ~=e-2K~,κ=e-2K とおいて,この2式を連立して解くと,
κ~=
2κ κ2+1
A~=
2(κ2+1) κ
であることが分かります。この変換を繰り込み変換といいます。(または,再帰関係式)
[3] スピン演算子が直接関係するκ^について,この繰り込み変換を繰り返し(=粗視化と最規格化を繰り返す)作用させると,下図(繰り込み変換の流れ)のように,原点(κ=0,K=∞,T=0)以外の点から繰り込み変換を(無限回)繰り返した場合,すべてP点(κ=1,K=0,T=∞)に収束していくことが分かります。このPは(安定な)固定点といいます。この漸近的挙動から絶対零度以外でこの系は高温相(無秩序相)にあることが示唆されます。
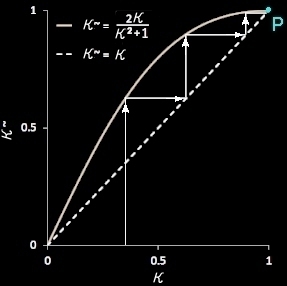 |
↑ : 粗視化 → : 再規格化 |
もう一つの固定点はκ=0の原点(収束点にならない不安定な固定点)であり,これは絶対零度T=0における完全な秩序状態に対応している考えられます。このように繰り込み群の方法によって完全秩序状態と完全無秩序状態の存在(場所)が明らかにされます。
この例の場合,厳密な解が分かっており,有難みは少ないのですが,近似的な解法しかわかっていないような場合でも臨界現象に関する情報を引き出すために威力を発揮します。2次元イジングモデルの場合であれば,有限温度(T≠0,∞)に固定点が存在することが導かれ,強磁性-常磁性相転移点の存在が示唆されます。
とりあえず,ここでは繰り込み群の概念の紹介だけに留め,一般的な繰り込み群のはなしと応用(スケーリング則など)は別の場所で ⇒ [#]
SUSTAINABLE TOKIWADAIGAK SINCE 2002
繰り込み群とならないような変換を例示しておけば,例えば,縦長の楕円を表すような関数だと繰り込み変換とはなりません。