##　クレプシュ･ゴルダン係数表の見方
f-denshi.com  更新日：

１．クレプシュ･ゴルダン係数表の見方

［１］　合成角運動量の固有ケットは前章で求めたように，

｜j m＞ ＝

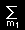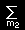｜j1j2；m1m2＞

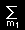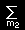＜j1j2；m1m2｜j m＞

と展開することができます。クレプシュ･ゴルダン係数［CG係数］の一覧はたいていの量子力学の教科書に表としてまとめられています[#]。ここでは，この係数の導出よりも，具体的な”クレプシュ･ゴルダン係数表”の使い方に慣れる方を優先しましょう。 まず，

0

［２］　まず，もっとも小さな系からです。下表は，

角運動量［j₁，m₁］   と   スピン角運動量［j₂，m₂］＝［1/2，±1/2］

との合成に必要なクレプシュ･ゴルダン係数です。

スピンとの合成
［j1，m1］と［1/2，±1/2］を合成する際のCG係数 ＜j1 1 ；m1m2｜jm＞ 2
j	m2＝ 1 のとき 2	m2＝− 1 のとき 2
＝j1＋ 1 2	A＝ j1＋m ＋(1/2) 1/2 2j1+1	B＝ j1−m ＋(1/2) 1/2 2j1+1
＝j 1− 1 2	C＝− j1−m ＋(1/2) 1/2 2j1+1	D＝ j1＋m ＋(1/2) 1/2 2j1+1

この表からは，合成後のケット｜j m＞ が基底｜j₁j₂；m₁m₂＞の線形結合で，　←　m₁＝m−m₂　に注意して，

｜j₁＋(1/2), m ＞＝A｜j₁j₂；m−(1/2)　(1/2)＞＋B ｜j₁j₂；m＋(1/2)　(−1/2)＞
                 ＝A｜m−(1/2)，(1/2)＞      ＋B ｜m＋(1/2)，(−1/2)＞

｜j₁−(1/2), m ＞＝C ｜j₁j₂；m−(1/2)　(1/2)＞＋D ｜j₁j₂；m＋(1/2)　(−1/2)＞
                 ＝C｜m−(1/2)，(1/2)＞       ＋D ｜m＋(1/2)，(−1/2)＞　　　

のように得られることを意味しています。もちろん，

j ＝j₁−(1/2)，j₁＋(1/2)　以外のときのクレプシュゴルダン係数 ＝ ０　。

［３］　具体的な計算を示しておきましょう。

具体例：　j₁ ＝ 1/2，m₁ ＝ ±1/2 のとき，    (⇔要するに２つのスピンの合成)

j	m2＝ 1 2	m2＝− 1 2
1 ＝ 1 ＋ 1 2 2	A＝ m＋1 1/2 2	B＝ −m＋1 1/2 2
0 ＝ 1 − 1 2 2	C＝− −m＋1 1/2 2	D＝ m＋1 1/2 2

ここで，とり得るm の値は

j ＝ 1　(三重項)　のとき，m　（＝m₁＋m₂ ）のとり得る値は，

(１)m＝1；    A＝1，   B＝0　　　⇒　　　| 1，1＞ ＝｜(1/2)，(1/2)＞
(２)m＝0；    A＝B＝	1  2	⇒　　　| 1，0＞ ＝	1  2		｜(1/2)，(1/2)＞＋｜(1/2)，(−1/2)＞
(３)m＝-1；  A＝0，    B＝1　   ⇒      | 1，-1＞＝｜(1/2)，(1/2)＞

の３とおり。

j ＝ 0　(一重項)　のとき，

(４)m＝0；  - C＝D＝

1  2

⇒　　　| 1，0＞ ＝

1  2

−｜(-1/2)，(1/2)＞＋｜(1/2)，(-1/2)＞

［４］　今度は，p 軌道が関与したときに重要となる，

角運動量［j₁，m₁］   と   p-軌道角運動量［j₂，m₂］＝［1，−1］，［1，0］，［1，＋1］

との合成に必要なクレプシュ･ゴルダン係数です。

［j1，m1］＋［1，m2＝±1，0］　の　C係数＜j11；m1m2｜jm＞
j	m2＝1	m2＝0	m2＝−1
j1＋1	(j1＋m)(j1＋m＋1) 1/2 (2j1＋1)(2j1＋2)	(j1−m＋1)(j1＋m＋1) 1/2 (2j1+1)(j1+1)	(j1−m)(j1−m＋1) 1/2 (2j1+1)(2j1+2)
j 1	− (j1＋m)(j1−m＋1) 1/2 2j1(j1＋1)	m 1/2 j1(j1＋1)	(j1−m)(j1＋m＋1) 1/2 2j1(j1＋1)
j1−1	(j1−m)(j1−m＋1) 1/2 2j1(2j1＋1)	− (j1−m)(j1＋m) 1/2 j1(2j1＋1)	(j1＋m＋1)(j1＋m) 1/2 2j1(2j1＋1)

具体例：

(２)　１＋1/2

(３)　　2＋1/2

(３)　1＋1

(４)　2＋1

これは問題集で，

［目次］