| 102 箱の中の自由粒子 | |
| f-denshi.com 更新日:07/05/31 | |
| サイト検索 | |
箱の中の自由粒子の量子力学的取り扱いは,量子(統計)力学を学ぶためのもっとも単純でもっとも重要な系です。これは水素原子のもっとも荒っぽいモデルにもなります。
1.箱の中の粒子(井戸型ポテンシャル)
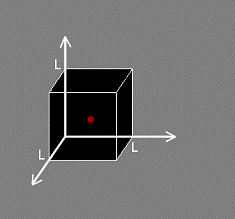 [1] 無限大のポテンシャルで1辺の長さが L の立方体に閉じこめられている粒子の量子力学状態を求めてみましょう。粒子のポテンシャルとハミルトニアンを,
[1] 無限大のポテンシャルで1辺の長さが L の立方体に閉じこめられている粒子の量子力学状態を求めてみましょう。粒子のポテンシャルとハミルトニアンを,
V(r)= 0 (箱の中: 0≦x≦L,0≦y≦L,0≦z≦L ) +∞ (箱の外: 上記の範囲外)
H =− h2∇2+V(r) 2m
として,シュレーディンガー方程式:
i h∂ ψ(r,t)=Hψ(r,t) ・・・・・ (1) ∂t
を解くのです。
[2] 空間方向の対称性,もしくは方程式の解 ψ(r,t) = ψ(x,y,z,t) が確率の積事象(〜 x=x0,かつ,y=y0,かつz=z0 である確率は,成分ごとの確率の積:ψ(x,t)ψ(y,t)ψ(z,t)となるに違いない!)を表していることを考えると波動関数は,
ψ(r,t)=ψ(x,t)ψ(y,t)ψ(z,t)
の形をしているとして計算を進めればうまくいきそうです。そのとき,立方体内部,すなわち,V(r ) = 0 のときのシュレーディンガー方程式は,
i h∂ ψ(x,t)ψ(y,t)ψ(z,t) = −
h2∂2 + ∂2 + ∂2 
ψ(x,t)ψ(y,t)ψ(z,t) ∂t 2m ∂x2 ∂y2 ∂z2
これを各変数について整理すると,
|
+ |
|
+ |
|
= 0 |
|||||||||||||||||||||||||||||||||||||||||||
| ψ(x,t) | ψ(y,t) | ψ(z,t) | ||||||||||||||||||||||||||||||||||||||||||||||
と,変数 x,y,z のいずれかのみを含む3つの項に分けて書くことができます。各変数は独立な変数なので,この方程式が成り立つためには,x,y,z それぞれについての項が 0 ,すなわち左辺の各項の値は 0 のはずです,つまり,
i h∂ ψ(x,t) =−
h2・ ∂2 ψ(x,t) ・・・・・・・(*) ∂t 2m ∂x2
が変数 y,z についても成り立たなければなりません。結局,問題1次元に還元されるのです
(右図参照)。 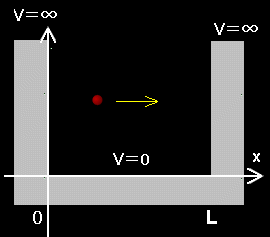
[3] この方程式を解くために,
ψ(x,t)=φ(x)exp[−i ωt]
とおいて(*)に代入すると, (↑定番のテクニック)
ω h・φ(x)exp[−i ωt]=−exp[−iωt]h2・ ∂2 φ(x) 2m ∂x2
となります。これを,exp[−iωt] で除せば,
− h2・ ∂2 φ(x)=ω hφ(x) ・・・・・ (**)2m ∂x2
| となります。 ここで,ω |
・ | ∂2 | とおいて, | |
| 2m | ∂x2 | |||
Hφ(x)=εφ(x) [定常状態のシュレーディンガー方程式]
この固有方程式は時間変数を含まない ”定常状態のシュレーディンガー方程式” とよばれます。また,量子力学で,φ(x),εはそれぞれ波動関数,エネルギー固有値と呼ばれ,
|φ(x)|2 はエネルギーεをもつ粒子を位置 x に見出す確率
と解釈されます。
[4] さて, 0<x<L においての(**) 式の一般解は,定数,c1,c2 を用いて,
φ(x)=c1 cos ax+c 2sin ax
となります。ただし,無限のポテンシャルをもつ境界 x=0 では,粒子の存在確率は 0 なので, φ(0) = 0 。つまり,
c1=0
同様な理由から,φ(L) = 0 ,⇒ φ(x)= c2sin aL = 0, つまり,
aL=nπ ( n =1,2,3,・・・ )
である必要があります。そこで,φ(x) = c2 sin (nπx/L) として,(**)に代入すると,
h2・ (nπ)2 c2 sin (nπx/L) =εc2 sin (nπx/L) 2m L2
したがって,
ε=ω h=(n hπ)2= h2k22mL2 2m
ただし,k = πn L
| が得られます。また,規格化条件, | { c2sin(nπx/L) }2dx = 1 より,c2= |
|
が求まります。 よって, | ||||||
φ(x)=
2 L sin kx
[5] 3次元のときは,(固有関数が3つの関数の積の形で与えられるとき,固有値は対応する3つの固有関数の和となるので)
|
この場合,一つのエネルギーεk に対して,二つ以上の状態(nx,ny,nz )が対応することがあり,そのようなとき,そのエネルギー準位は縮退しているといいます。
j エネルギー
ε'j状態数
Δj状態
(nx,ny,nz )1 1 1 (1,1,1) 2 6 3 (2,1,1),(1,2,1),(1,1,2) 3 9 3 (1,2,2),(2,1,2),(2,2,1) 4 11 3 (3,1,1),(1,3,1),(1,1,3) 5 12 1 (2,2,2) 6 14 6 (1,2,3),(1,3,2),(2,1,3),(2,3,1),(3,1,2),(3,2,1) : : : ・・・・
↑エネルギーは,εj = ( hπ)2ε'jとして。 2mL2
| [6] 一次元の場合の波動関数,φ(x,t)= |
|
sin (nπx/L)を図示すると右のとおりです。 ここで, | ||||||
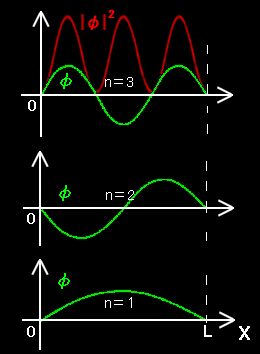
λ= 2L = 2π n k
を波長として定義します。つまり,n=1のときは波長が2Lの定在波,n=2のときは波長がLの定在波などとなっています。
n=3のエネルギー準位については,電子の存在確率に比例する|φ|2も重ね書きしています。これをみると電子の存在確率が0となる節が2つ存在することがわかります。その結果は一つの電子が3つの領域に分かれて存在すると解釈できるような状況です。このような性質は,電子が波として存在しており,
電子が自分自身と干渉して定在波をつくっている
と解釈することができます。電子のこのような波としての側面を物質波といいます。つまり,物質は存在そのものが波としての性質をもっており,干渉することで,その存在がなくなったり強め合ったりすることがあるのです。
したがって,2つのポテンシャルの壁にはさまれたような状況では,定在波を作る条件を満たすときのみ電子は安定に存在することができ,その条件を満たさない場合は自分自身と干渉して打ち消しあってしまいます。言い換えれば,そのような状態で電子は存在することがないということです。
このような事情は今考えているモデルに特有のことではなく,シュレーディンガー方程式の厳密解が存在する実在の水素原子中の電子においても当てはまります。
(局在化した電子だけでなく,並進運動する電子についても波としての性質を確かめることができ,一つの電子が2つのスリット(穴)を同時に通過してその先で干渉する (存在確率に空間的な斑(むら)ができる) ようなことも起こります。)
複素数解
ψ(x,t)=φ(x)exp[−i ωt]において,
φ(x)=exp(i kx)
とおくときは,これを定常状態のシュレーディンガー方程式に代入して,
− h2(i k)2 φ(x)=εφ(x) 2m
すなわち,
ε= h2k2← 本文中と同じ 2m
存在範囲が長さLという境界条件として,周期境界条件,
φ(0)=φ(L) ⇔ 1=exp(i kL)
を課せば,
kL=2πn ただし,n=整数
3次元で表すと,
(kx,ky,kz) = 2πnx , 2πny , 2πnz 
L L L