
 |
�X�@���[�ϕ����̉��p |
| f-denshi.com �ŏI�X�V���F�@�@04/01/07 | |
| �T�C�g���� | |
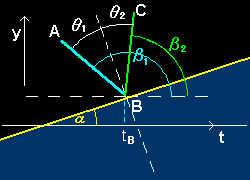
[1]�@���̔��˂̖@����ϕ���������(�t�F���}�[�̌���)���瓱���Ă݂܂��傤�B���͉E���}�ł�A������˂��āC�_B�Ŕ��˂��CC�_�֔����Ă����Ƃ��܂��B���˓_B�ł̘A��������C
��(tB-0)����(tB+0)
| �@�@�i[��(t)]�� | F[t,y(t),y�f(t)]dt |
|
| �@�@�i���� | Fdt�{�� | Fdt��0 |
y��g(t)
| �@�@�� | Fdt��[Fy�f(g�f�|��*�f)�{F]��tB |
| �@�@�� | Fdt��[Fy�f(g�f�|��*�f)�{F]��tB |
�@
[Fy�f(g�f�|���f)�{F]��tB-0��[Fy�f(g�f�|���f)�{F]��tB+0
| �@�@�i[��(t)]�� | F[t�Cy(t)�Cy�f(t)]dt |
| �@�@�i[��(t)]�� | (1�{y�f2)1/2 | dt | |
| �@V(x�Ct) |
| �@ | �@�@1�@�@ | (1�{y�f2)1/2�{ | (g�f�|���f)���f | ||||
| V(x�Ct) | (1�{y�f2)1/2 | tB-0 |
| �@�@�@�@�@�@�@�� | �@�@1�@ | (1�{y�f2)1/2�{ | (g�f�|���f)���f | ||||
| V(x�Ct) | (1�{y�f2)1/2 | tB+0 |
��
| �@�@�@ | �@1�{g�f���f | �� | �@1�{g�f���f | ||||||
| (1�{y�f2)1/2 | tB-0 | (1�{y�f2)1/2 | tB+0 |
�����ŁC�e����(�X��)�͉E�}�̊p�x���C��1�C��2�Ɖ��̂悤�ɊW�Â�����̂ŁF
���@g�f(tB)��tan���Cy�f(tB-)��tan��1�Cy�f(tB+)��tan��2
| �@�@�@ | �@1�{tan��tan��1 | �� | �@1�{tan��tan��2 | ||||
| (1�{tan2��1)1/2 | (1�{tan2��2)1/2 |
��
| �@�@�@ | �@1�{tan��tan��1 | �� | �@1�{tan��tan��2 | ||||
| �bcos��1�b | �bcos��2�b |
�����܂ŗ���C���Z���̖��ł��ˁB���ǁC������p���ē��ˊp��1�C���ˊp��2�ɒ����ƁC
�@�@�@�@�@��1�|������/2�{��1�C�@��2�|������/2�|��2�@
���˂̖@���F
��1����2
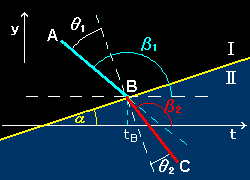 [1]�@1�D���̔��˂̏ꍇ�Ƃ̈Ⴂ�́C���ˌ��͗̈�T�C���܌��͗̈�U�ɂ���C���ꂼ��̗̈�Ō��̑��x���قȂ�C
[1]�@1�D���̔��˂̏ꍇ�Ƃ̈Ⴂ�́C���ˌ��͗̈�T�C���܌��͗̈�U�ɂ���C���ꂼ��̗̈�Ō��̑��x���قȂ�C
| V(x�Ct)�� | V1�@(�̈�T) | |
| V2�@(�̈�U) |
�Ƃ������Ƃł��B���������āC�e�̈�ō�p���ɓY���������Ă��ꂼ��F1�CF2�Ƌ�ʂ���K�v������܂��B
| �@�@F1�� | (1�{y�f2)1/2 |
| V1 |
| �@�@F2�� | (1�{y�f2)1/2 |
| V2 |
���ˊp��1�C���܊p��2���̊W�͉E�}�̒ʂ�Ƃ��܂��B��p�ϕ���
|
�̋ɒl�����́C
| �@�@�i���� | F1dt�{�� | F2dt��0 |
�ƂȂ�܂��B���˂̏ꍇ�Ɠ��l�ɉ��f���̏���[#]���K�v�ł��B
[F1y�f(g�f�|���f)�{F1]��tB-0��[F2y�f(g�f�|���f)�{F2]��tB+0
���Ȃ킿�C
| �@ | 1 | (1�{y�f2)1/2�{ | (g�f�|���f)���f | |||
| V1 | (1�{y�f2)1/2 | tB-0 |
| �@�@�@�@�@�@�@�� | 1 | (1�{y�f2)1/2�{ | (g�f�|���f)���f | ||||
| V2 | (1�{y�f2)1/2 | tB+0 |
���@g�f(tB)��tan���Cy�f(tB-)��tan��1�Cy�f(tB+)��tan��2�C
| �@�@�@ | �@1�{tan��tan��1 | �� | �@1�{tan��tan��2 | ||||
| V1(1�{tan2��1)1/2 | V2(1�{tan2��2)1/2 |
���@��1�|������/2�{��1�C�@��2�|������/2�{��2�@�Ȃ�W��p���āC
V2 �@�� �@sin��2 V1 �@sin��1

�����̖@���͓d���C�w�ł́CB�ɂ�����d���g�̓d��Ǝ���̐ڐ������̘A�����Ȃǂ�����������Ƃ��ł��܂��@[#]�B
���C�������