８　微分形式の積分
f-denshi.com  最終更新日：22/12/15   校正中

１．微分形式の積分の定義

［１］　厳密には細かい条件を考慮しなければいけないが，とりあえず簡明に，k次微分形式の積分を次のように定義する。

［２］

1次微分形式の場合

φ＝c(t)＝(c₁(t)，…，c_m(t))
   ＝r(t)＝(ｘ₁(t)，…，x_m(t))　∈R^m　　←　R^m内の曲線
　　　　( a≦t≦b )

と表すと，

ω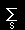＝		fs dxs

のφに沿った積分は，

∫ r(t) ω≡	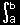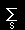fs (r(t) )		dxs dt		dt

＝

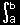f1(r(t))

dx1(t)

＋f2(r(t))

dx2(t)

＋･･･＋fm(r(t))

dxm(t)

dt　　　　(1)

dt

dt

dt

と表され，初等解析学で学ぶ 「線積分」 になります。

特に，r(t)＝x₁(t)＝t　(数直線)　の場合は，

∫ r(t) ω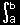＝ f(t)dt

となり初等解析学で学ぶ 実数関数の積分に帰着されます。

[ ３] 　また，1次微分形式は引き戻しφ^*＝r^*　を用いると，

φ*ω＝φ*(		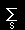fs dxs)

＝		fs(r(t))dxs(t)

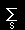＝		fs(r(t)) dxs(t) dt dt

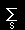と表すことができます。

これを(1)と比較して，( r をφと書いて )

∫ φ ω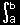＝ φ*ω

と書いてよいことが分かります。

［４］　特に，1次微分形式が

ω＝df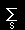＝		∂f		dxs
		∂xs

と表されるときは，合成微分の公式が使えて，

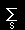∫ r(t) df＝ ∫ r(t)				∂f		dxs
				∂xs

＝

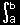∂f(r(t))

∂x1(t)

＋

∂f(r(t))

∂x2(t)

＋･･･＋

∂f(r(t))

∂xm(t)

dt

∂x1

∂t

∂x2

∂t

∂xm

∂t

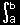＝			df(r(t))	dt
			dt

＝f(r(b))−f(r(a))

すなわち，

∫ r(t) df ＝f(r(b))−f(r(a))

が成り立ちます。これは初等解析学で学ぶ微分積分学の基本定理，

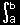		f’(x)dx	＝f(b)−f(a)　　　　[微分積分学の基本定理]

に対応しています。

これは，r(t)の境界という意味で∂r(t)という記号を用いれば，

∫	r(t)	df	＝f(r(b))−f(r(a))	＝∫∂r(t) ｆ

↓↑

∫	φ	dω	＝∫∂φω　　　［ストークスの定理］

と書けば，ストークスの定理でω＝0次形式の場合に対応していますが，詳細は一般次元の定理として，次ページで説明します。

［５］　

3次元多様体の2次微分形式の積分

＝f₁₂ dx₁Λdx₂＋f₁₃ dx₁Λdx₃＋f₂₃ dx₂Λdx₃

＝f₁₂ dx₁Λdx₂＋f₃₁ dx₃Λdx₁＋f₂₃ dx₂Λdx₃

(f₁₃＝−f₃₁)

φ＝r(t₁,t₂)
　 ＝(ｘ₁(t₁,t₂)，ｘ₂(t₁,t₂)，x₃(t₁,t₂)) ∈ R³　←　R^m内の曲面

として計算を進めると，

∫ φ ω≡ ∫ [ ] Σ s1<s2	fs1s2 (r(t1,t2)) det		∂xs1 ∂xs1 ∂t1 ∂t2 ∂xs2 ∂xs2 ∂t1 ∂t2		dt1dt2

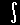＝ b2 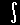b1 a2 a1

f12 (r(t1,t2))

∂x1 ∂x1 ∂t1 ∂t2 ∂x2 ∂x2 ∂t1 ∂t2

＋f31 (r(t1,t2))

∂x3 ∂x3 ∂t1 ∂t2 ∂x1 ∂x1 ∂t1 ∂t2

＋f23 (r(t1,t2))		∂x2 ∂x2 ∂t1 ∂t2 ∂x3 ∂x3 ∂t1 ∂t2				dt1dt2

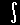＝ b2 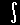b1 a2 a1

f ・

∂r

×

∂r

dt1dt2

∂t1

∂t2

と表されます。これは初等解析学で学ぶ「面積分」に相当することが分かります。

ただし，「・」は内積を表し，

f ＝f₁₂(r(t₁,t₂))，f₁₃(r(t₁,t₂))，f₂₃(r(t₁,t₂))

で定義されるベクトルです。

［６］

3次元多様体の3次微分形式の積分

ω＝f₁₂₃ dx₁Λdx₂Λdx₃

φ＝r(t₁,t₂,t₃)
　 ＝(ｘ₁(t₁,t₂,t₃)，ｘ₁(t₁,t₂,t₃)，x₃(t₁,t₂,t₃)) ∈ R³

とします。

この場合，φはR³上の座標変換 (積分変数の変換) とみることもでき，

特に恒等変換φ＝I  (x_s=t_s) であれば，行列式は１なので，

∫	φ	f123 dx1Λdx2Λdx3≡	＝ b3 b2 b1 a3 a2 a1	f123 (x1,x2,x3)dx1dx2dx3

と書けるので，右辺は初等解析学での重積分，もしくは 「体積分」 に他なりません。

２．積分の定義の妥当性

［１］  はじめに１次微分形式の積分の定義は初等的な解析学との整合性が取れていることを確認しましたが，微分形式の積分は 「どのような座標系で計算しても同じ値となる」 ことを見ておくことも重要です。

微分形式が，

ω＝f(x₁,…,ｘ_n)(dx₁)Λ(dx₂)Λ…Λ(dx_n)
　　＝g(y₁,…,y_n)(dy₁)Λ(dy₂)Λ…Λ(dy_n)

とそれぞれの局所座標で表されるとき，余接空間の基底変換を

dyj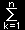＝		∂yj			dxk　　　［基底変換の公式］
		∂xk

とすれば，これを最初の式に代入することで，

(dy₁)Λ(dy₂)Λ…Λ(dy_n)

＝

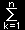∂y1

dx1Λ

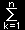∂y2

Λdx2…Λ

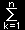∂yn

dxn

∂xk

∂xk

∂xk

＝	Σ	sgn(σ)	∂y1		･･･		∂yn			(dx1)Λ(dx2)Λ…Λ(dxn)
	σ∈Sn		∂xσ(1)				∂xσ(n)

＝	∂(y1,…,yn)			(dx1)Λ(dx2)Λ…Λ(dxn)
	∂(x1,…,ｘn)

のような関係があることが分かります。　ここで，座標変換のヤコビアンは，

∂(y1,…,yn) ＝ ∂(x1,…,ｘn)			∂y1 ････ ∂y1 ∂x1 ∂xn
			：　　　　　　：
			：　　　　　　：
			∂yn ････ ∂yn ∂x1 ∂xn

と行列表示されます。

一方，ｆ と g については，この結果を最初のωの式に代入することで，

f(x1,…,ｘn)＝	∂(y1,…,yn)		g(y1,…,yn)　　････　[*]
	∂(x1,…,ｘn)

の関係が容易に見出すことができます。

［２］　[*]　を利用すると，微分形式の積分に現れる項ごとの積分は，

∫g(y_s1,…,y_sk)dy_s1…dy_sk

↓　重積分の変数変換公式

＝∫g(ys1(xs1,…,xsk),…,ysk(xs1,…,xsk))		∂(ys1,…,ysk)		dxs1…dxsk
		∂(xs1,…,xsk)

↓　ヤコビアン ＞ 0　　

＝∫g(ys1(xs1,…,xsk),…,ysk(xs1,…,xsk))	∂(ys1,…,ysk)		dxs1…dxsk
	∂(xs1,…,xsk)

＝∫f(x_s1,…,x_sk)dx_s1…dx_sk　

と計算でき，これより局所座標の取り方に依存せず，積分値は同じ値を取ることが分かります。

もちろん，それらの和として表される微分形式の積分値も局所座標のとり方によらず定まります。

結局，最初に示した微分形式の積分の定義が　well-defined　であることが分かりました。

［３］　　最後に全体を見通した話しをしておくと，

（１）　微分形式になぜ行列式が現れるのかといえば，微分形式が交代性をもつ多重線形写像であり，交代性をもつ多重線形性は行列式を用いて表すことができるからである。

（２）　一方，線積分，面積分，体積分はそれぞれ，線密度，面密度，体積密度に依存する量が積分範囲全体でどれほどになるのかを積算する計算方法である。そのとき，方向付きの微小長さ，微小面積，微小体積を用いて計算を行うが，それらの量はその次元と同じ次数の行列式を用いて表すことができる。

この２つの性質によって，つまり，行列式の性質を介して微分形式の積分と体積分等が結び付けられているのです。

これらの関係は３次元より大きな次元の多様体，ユークリッド空間に対しても拡張できることは，行列式の性質から容易に分かります。つまり，ｎ次元多様体の体積分，面積分がn次，n−1次微分形式の積分で計算されます。

n次微分形式の積分

⇔

ｎ次行列式

⇔

ｎ次元体積分

目次へ