| 4-4 埋め込み・はめ込み | ||
| f-denshi.com [目次へ] 最終更新日:21/07/06 校正中 | ||
| サイト検索 | ||
[1] まず,部分多様体の定義を再掲しておきます。
|
定義 部分多様体 m次元 Cr級多様体 Mの部分集合N (N⊂M) の任意の点p に対して,p を含む Nの座標近傍 (U;x1,x2,…,xn ) が存在して, N ∪ U={ (x1,x2,…,xm )= (x1,x2,…,xn,0,…,0) } と表すことができるとき,N を Mの n次元 Cr級部分多様体という。 |
難しい用語は含まれていませんが,多様体(位相空間)が自由に伸び縮みする (距離が入っていない) 空間 ということから注意すべき点がいくつかあります。
[2] ここで,ある多様体N を多様体Mの部分集合に対応させることを考えてみましょう。
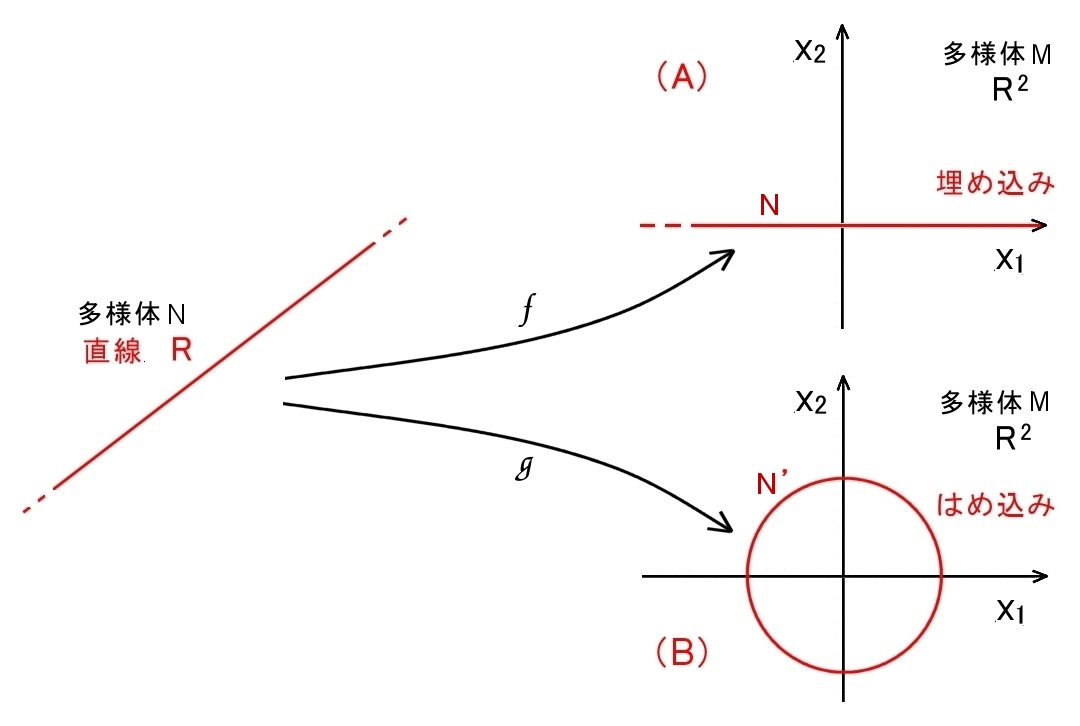
具体的に2次元 C∞級多様体N として,2次元ユークリッド平面 R2を考えると,
(A) x1軸 (N) ,
(B) 半径1の円 (N’)
はR2の1次元部分多様体であることは容易に分かります。
(B)の場合,x1>0の領域であれば,そのx2成分を用いて,(x2,0) を局所座標とすればよい・・・。
そこで,多様体N としての直線R から部分集合 N,N’上への写像を直感的に考えてみます。
(A)は埋め込みと呼ばれる写像なのですが,直線RをR2の x1軸にぴったりと合わせてやれば,位相も含めて1対1に重ね合わせられることは直感的にすぐに分かります。つまり,
f: t∈R ⇒ (t,0)∈R2
(B)は直線R を,
g: t∈R ⇒ (cost,sint)∈R2
によって写しており,直線がR2の円の中に巻きつくように収納されていることが分かりますが,g(x)=g(x+2π) の周期性があり,1対1写像ではありません。
よって,(A)と(B)とでは,明らかに状況が違うので区別して考える必要があります。
局所的に制限してみれば,(B) も1対1写像になっているので,(A)は(B)の特別な場合として分類することができます。
そこで,(B)のような写像が満たす最低限の条件として,はめ込みを定義します。
[3]
|
定義 はめ込み 多様体NからMへのCr級写像 g が,すべての点p∈N において,gの微分 (dg)p: Tp(N) → Tf(p)(M) が1対1写像であるとき,g をNからMへのはめ込みという。 |
具体的には,(dg)p の行列表現が [*] ’で示したヤコビアン(Jg)p の階数がNの次元nであるとき,g をはめ込みといいます。g が局所的に1対1対応するための条件です。gは全域では1対1である必要はありません。
[4] 特に多様体N の像がMの部分集合である曲線C(t) であれば,
|
命題 Cr級写像g が曲線C(t) で表される多様体Mへのはめ込みであるための必要十分条件は,
が成り立つことである。 |
これを (B)について確かめてみると,t∈R について
C(t)= g(t)= g1(t) = cos t ⊂R2 g2(t) sin t
であるから,
(Jg)p=
∂g1 (p) ∂t = −sin t
∂gn (p) ∂t cos t
となって,これはすべての t ∈Rに対して 0 とならない(階数は2)。つまり,(B)はめ込みです。
(A)も t∈R について,
f(t)= f1(t) = t f2(t) 0
(Jg)p= 1 ≠0 0
なので,これははめ込みです。またこれは埋め込みでもあることは後で示します,
[5] 次に埋め込みの定義です。
|
定義 N からM へのはめ込み f の像f(N) に M の相対位相 [#] を入れて,f が同相写像であれば,f
を埋め込みという。 |
(B)の場合で確かめると,
f: t∈R ⇒ (t,0)∈R2
が通常の実数の位相において,同相写像であることは自明ですね。
[6] 別の定義です。
|
定義 n次元Cr級多様体N から m次元Cr級多様体 M への写像 f : N ⇒ M が Cr級微分同相写像であるとき,f(N)をCr級の埋め込みという。
|
「多様体Nの埋め込みは,多様体Nと同じ次元かそれ以上の次元の多様体 (n≧m) でなければならない」 ことは定義からすぐに分かります。
[7] 部分多様体と埋め込みとの関係
|
命題 m次元 Cr級多様体M の n次元 Cr級部分多様体 [#] を N とするとき,包含写像, i : N ⇒ M はCr級の埋め込みである。 |
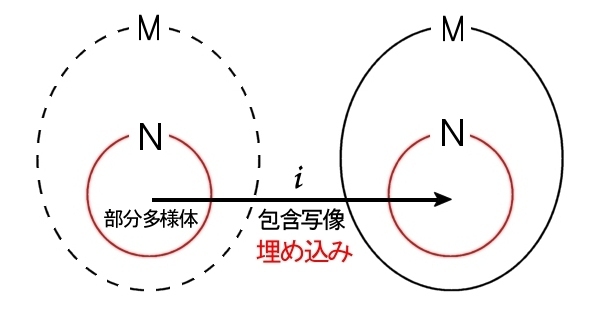
要するに,N を f で M に埋め込むことができれば,f(N) は M の部分多様体となっているということです。
[8] 2次元多様体のはめ込み・埋め込みの例をあげておきます。
| 2次元多様体 同色矢印の辺を同一視 |
2次元 | 3次元 | 4次元 | ||||
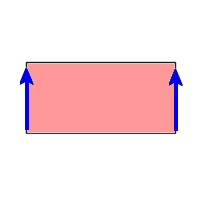 |
⇒ | 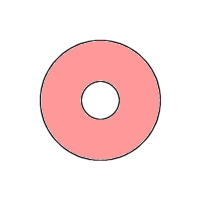 |
|||||
| 円柱側面 | R2へ埋め込み可能 | ||||||
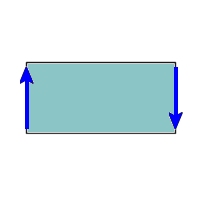 |
⇒ | 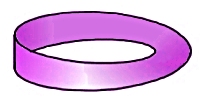 |
|||||
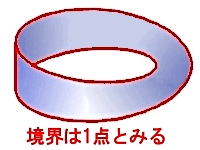
| メビウスの帯 | R3へ埋め込み可能 | ||||||
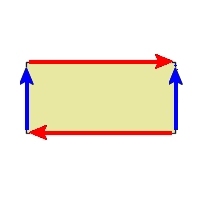 |
⇒ | 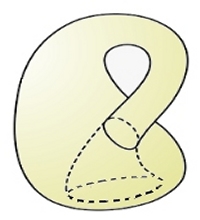 |
⇒ | この動画 で見える化 (外部サイト) |
|||
| クラインの壷 | R3へはめ込み可能 | R4へ埋め込み可能 | |||||
 |
 ボーイの曲面 (外部サイト) |
||||||
| 射影平面RP2 | R3へはめ込み可能 | R4へ埋め込み可能 |