ユークリッド幾何学（復習）
f-denshi.com  最終更新日：
サイト検索

円周角の性質

　  　　　　　

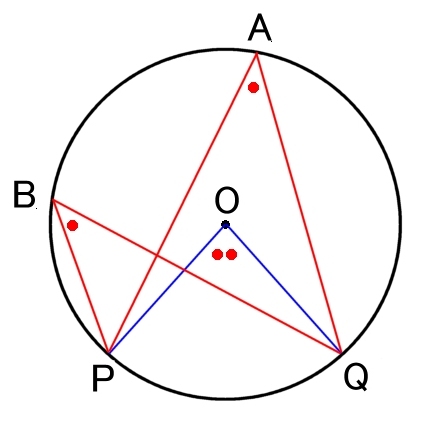
円周角∠A，∠B と中心角∠POQ について，

2∠A ＝ 2∠B ＝ ∠POQ

証明　　次の2通りを考えればよい。

［１］

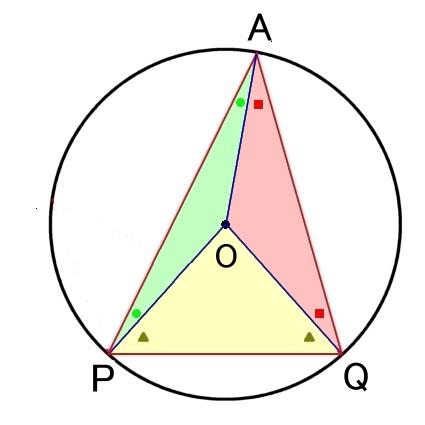
上図のように △APQ を３つの２等辺三角形の和と考えれば，

2 (●＋■＋▲)＝180°

これより，

∠POQ ＝180°−2▲
　　　　　＝2 (●＋■)
　　　　　＝2∠PAQ

［２］


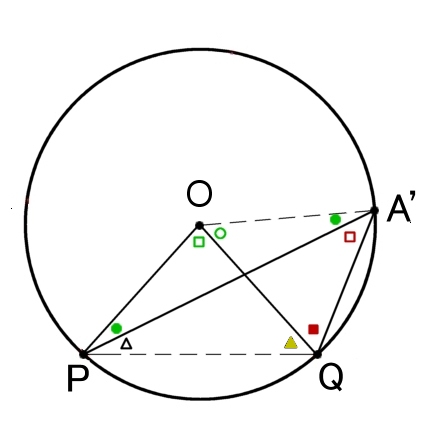
△OPQ，△OQA'，△OPA'が二等辺三角形であることに注意して，

□＋●＋△＋▲＝180°⇒　□＋2(●＋△)＝180°･･･(1)
○＋■＋□＋●＝180°⇒　○＋2(□＋●)＝180°･･･(2)
○＋□＋●＋●＝180°　　　　　　　　　　　　･･･(3)

(1)＋(2)−2×(3)　より，

2□−□＝0

すなわち，　2∠PA'Q＝∠POQ

また，円周角について，

∠A＝∠B

はどちらも同じ中心角を持つので前半の結果より成り立つ。　　(終)



内接四角形の対角


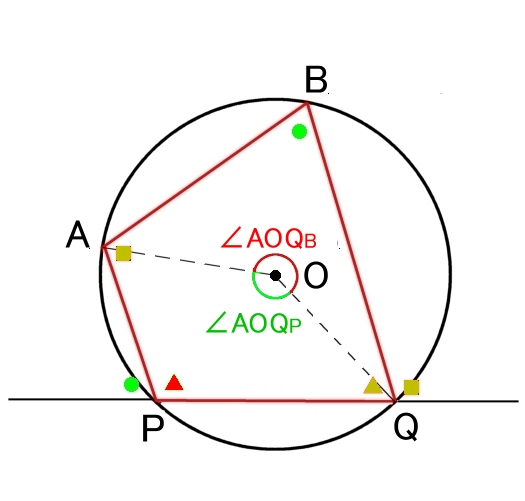
対角の和 ： ∠A＋∠Q ＝ 180°＝∠B＋∠P

証明　　

円周角と中心角の関係より，

2 (∠B＋∠P) ＝∠AOQP＋∠AOQB ＝ 360°　　(終)



方べきの定理



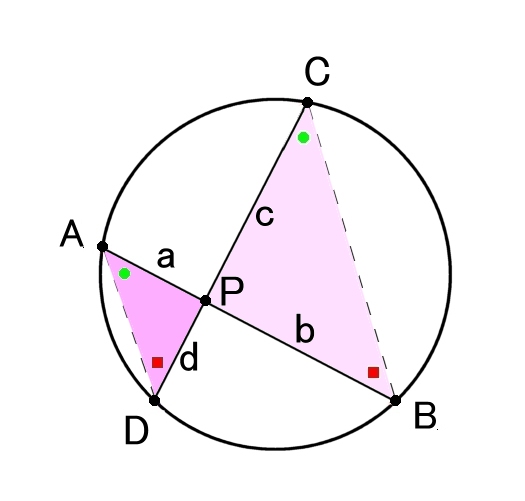
円周上の４点について，線分AB，CDの交点をP，線分
PA，PB，PC，PDの長さをそれぞれ a，b，c，d とするとき，

公式　　ab ＝ cd　　　　

証明

△PAD ∽ △PCB　なので，

PA：PC＝PD：PB　⇔　a：c ＝ d：b
　　　　　　　　　　　 ⇔　ab ＝ cd 　　　　　　(終)



三角形の角２等分線

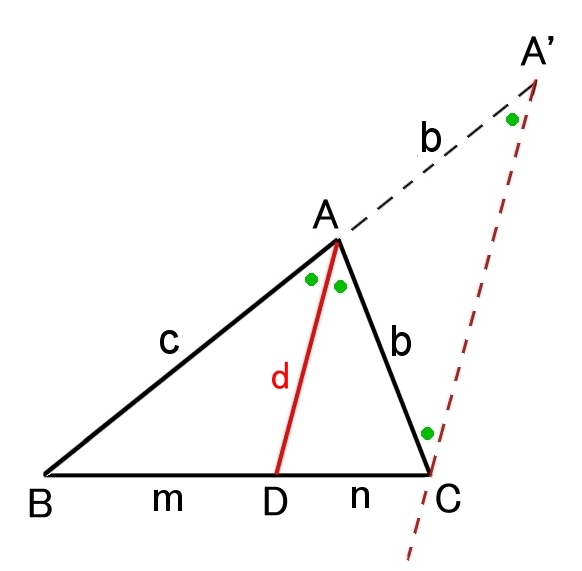
公式１　  c：b ＝ m：n　

証明

図のとおりADとA’Dを平行とする。

△ABD ∽ △A’BC　⇔　c：(c+b) ＝ m：(m＋n)　
　　　　　　　　　　　　　⇔　m(c+b) ＝ c(m＋n)　
　　　　　　　　　　　　　⇔　bm ＝ cn　
　　　　　　　　　　　　　⇔　c：b ＝ m：n　　　　　(終)

公式２　d2 ＝ bc−mn

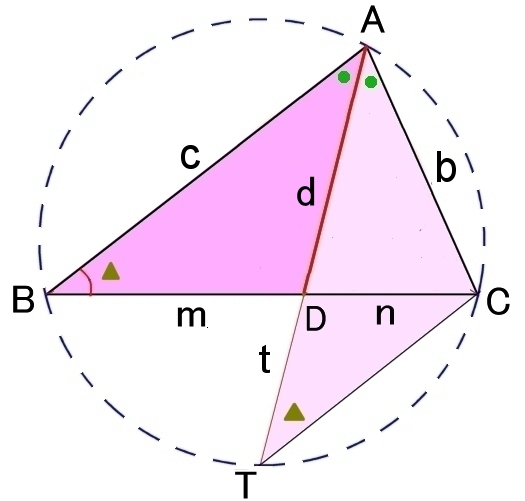
△ABCの外接円とADを延長した直線との交点をTとすると，

dt＝mn     　　　　[方べきの定理]

また，△ABDと△ATCは相似なので，

c：AT＝d：b　⇔　bc＝d×AT
　　　　　　　　　　　　＝d (d＋t)
　　　　　　　　　　　　＝d2＋dt
　　　　　　　　　　　　＝d2＋mn　　　(終)

この２つの公式はAの”外角の２等分線”が BC の延長線上右側の点 で交わる場合でも成り立つ。




中線定理

下図，辺BCの中点をMとし，AM＝d，BM＝CM＝m＝a/2　とすれば，

　b2＋c2 ＝ 2(d2＋m2) ＝ 2d2＋a2/2

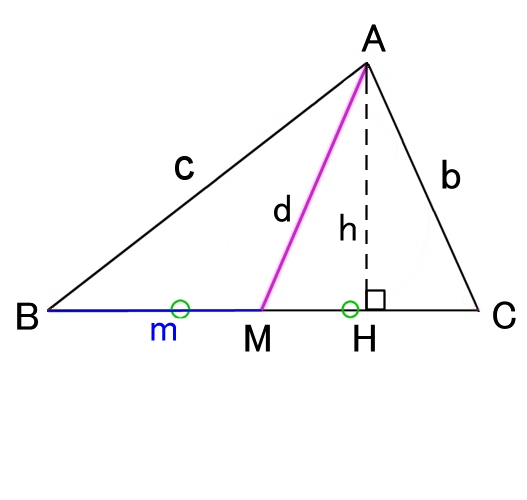
証明

Aから BCへ垂線AH を下し，その長さをh とする。

△ABH，△ACH，および，△AMH に三平方の定理を適用して，

c2 ＝ h2＋(m＋MH)2　　　･･･(1)
b2 ＝ h2＋(m−MH)2　　　･･･(2)

および，

h2＋MH2 ＝ d2　　　　 　　･･･(3)

(1)＋(2)＋2×(3) を計算すれば求めるべき式となる。



三角形の外心，内心，垂心，重心　の定義

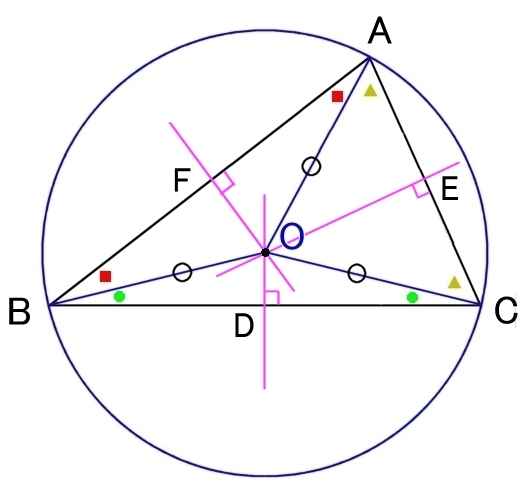
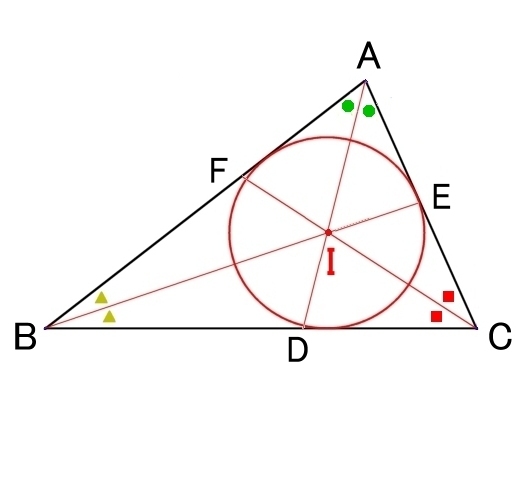
外心 内心
O：３辺の垂直二等分線の交点 I ：３つの角の二等分線の交点
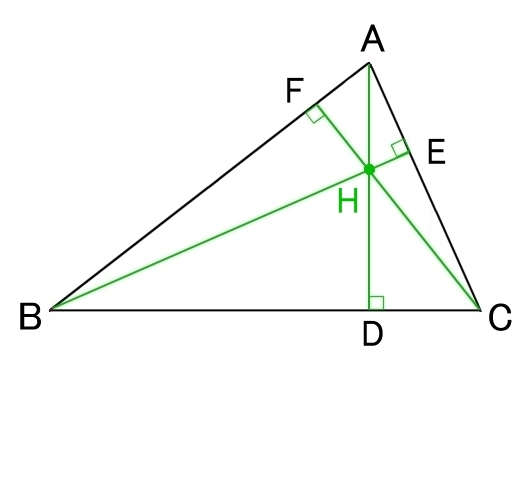
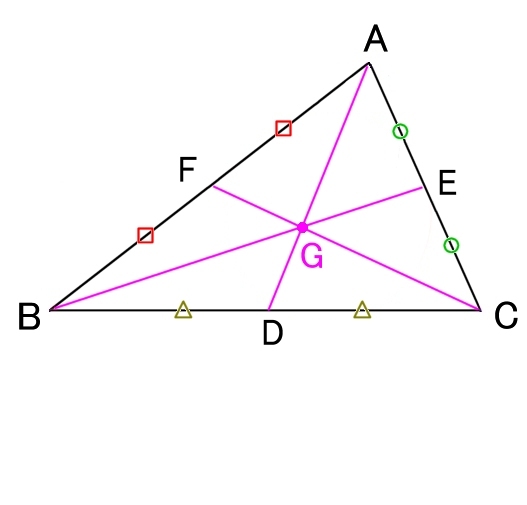
垂心 重心
H ：３つの頂点から対辺への垂線の交点 G ：３つの中線の交点


この定義が正当性は次の定理で保証される

定理　上記の３直線はいずれの場合も１点で交わる。

証明は下図がヒント。

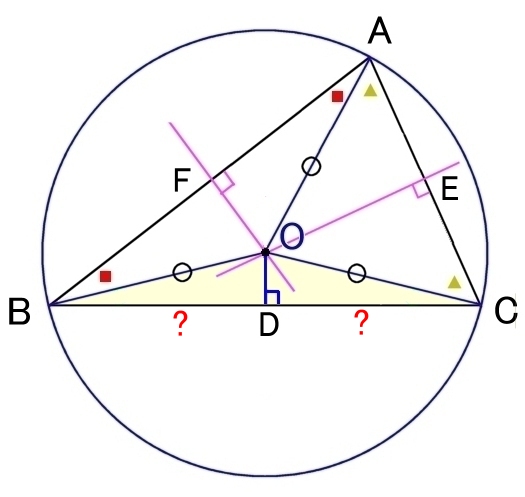
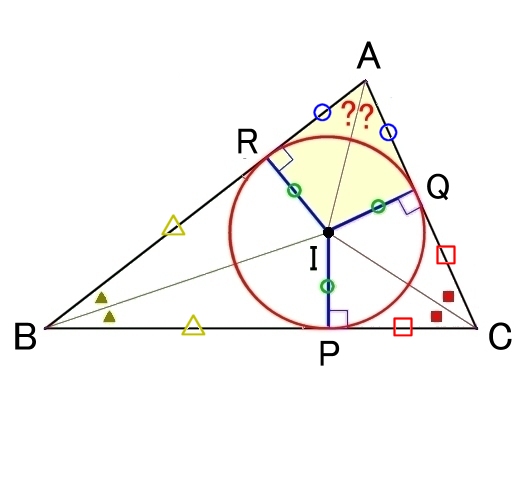
BD＝DCを示す ∠RAI＝∠QAIを示す
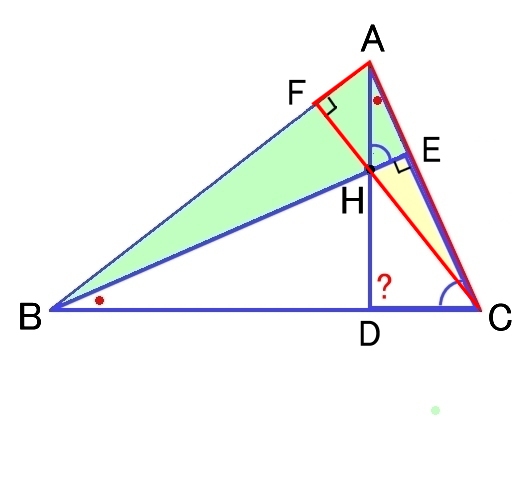
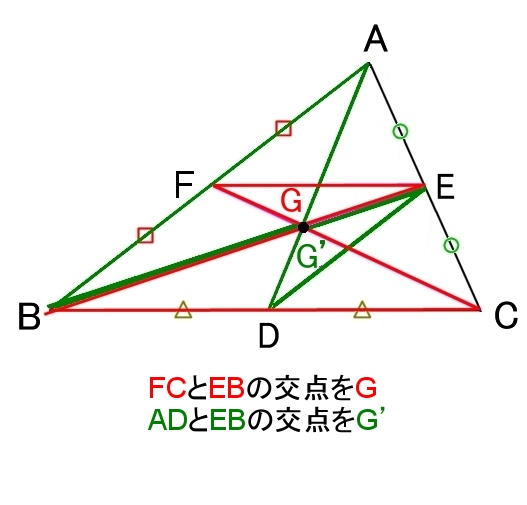
∠HDC＝90°を示す G＝G’を示す


三角形の重心の公然の秘密

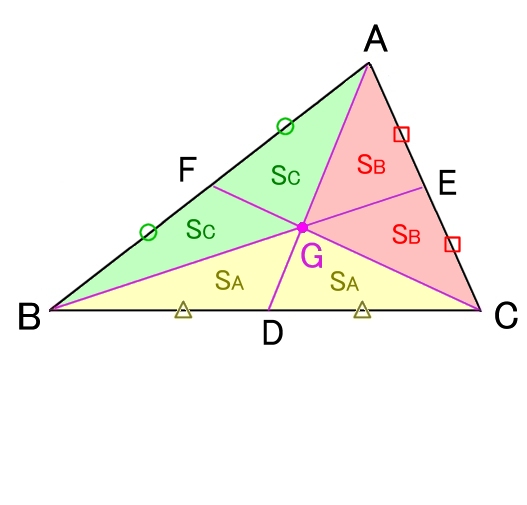
SA ＝ SB ＝ SC   　　[Gで面積を３等分]　


三角形の頂点と外心，内心，垂心，重心との距離

外心

AO ＝R ＝ a ＝ b ＝ c
2sinA 2sinB 2sinC
　　　　　＝ abc
4 s(s-a)(s-b)(s-c)

ただし，

s＝ a＋b＋c
2

内心
AI ＝4R sin(B/2) sin(C/2)
　　＝
bc(−a＋b＋c)
a＋b＋c
PI＝
s(s-a)(s-b)(s-c)
　[内接円の半径]
s

垂心

AH ＝2R｜cosA｜＝ a ｜cosA｜
sinA

重心

GA ＝
−a2＋2b2＋2c2
3

証明　　　　省略



外心と内心の距離

三角形の外接円の半径を R ，内接円の半径を r ，外心 O と内心 I の距離を d とすれば，

d2＝R 2−2Rr　⇔　2Rr ＝ (R＋d)(R−d)　[オイラーの定理]


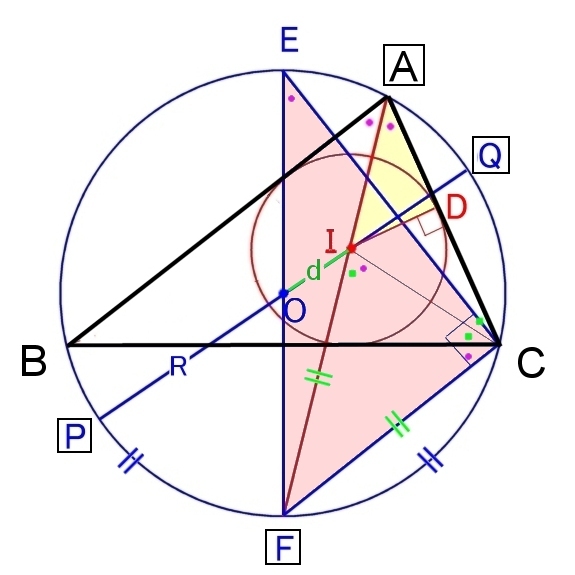
証明

図のように補助線を書き入れると，

△ADI　∽　△ECF

⇔　　AI：EF ＝ DI：CF
⇔　　AI：2R ＝  r：IF

⇔　　2Rr  ＝　AI･IF
              　　 ↓　方べきの定理
⇔　　2Rr　＝ QI･IP
⇔　　2Rr　＝ (R−d)(R＋d）


正弦定理

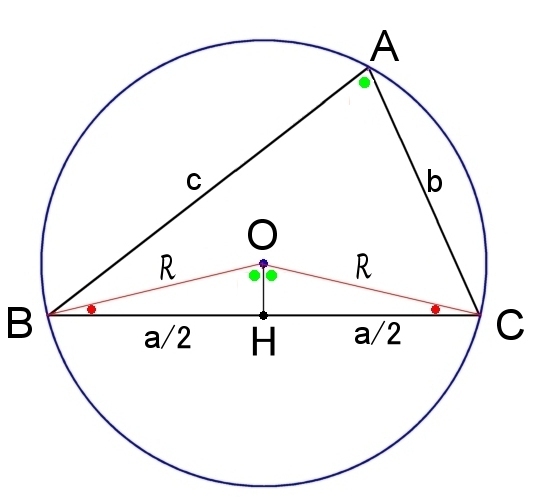
R ＝ a ＝ b ＝ c
2sinA 2sinB 2sinC

証明

外心からBCへ下した垂線の交点をHとすると，

円周角の定理から ∠COH＝∠A，および，∠CHO＝90°なので，

a ＝R a/2 ＝R sinA
2 R

他の角の場合も同様。



余弦定理

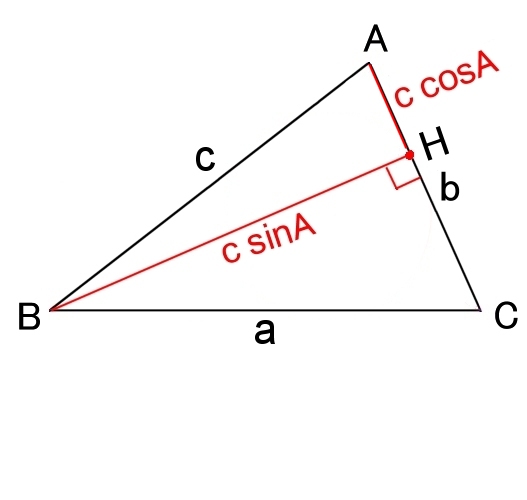
a2＝b2＋c2−2bc cosA
b2＝c2＋a2−2ca cosA
c2＝a2＋b2−2ab cosA

証明

CからACに垂線を下して，その点をHとする。

△HCBに三平方の定理を用いると，

a2＝(b−c cosA)2＋(c sinA)2
   ＝b2＋c2−2bc cosA
　＝b2＋c2−2b AH

他２式も同様。



三角形の面積

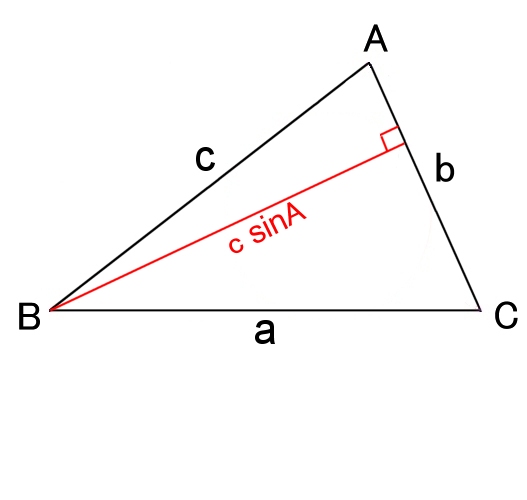
S　＝ bc sinA
2
　　＝ s(s-a)(s-b)(s-c) 　　　[ヘロンの公式]

ただし，

s＝ a＋b＋c
2

ヘロンの公式は余弦定理を用いて証明します。


体積＝1の立方体に内接する正四面体

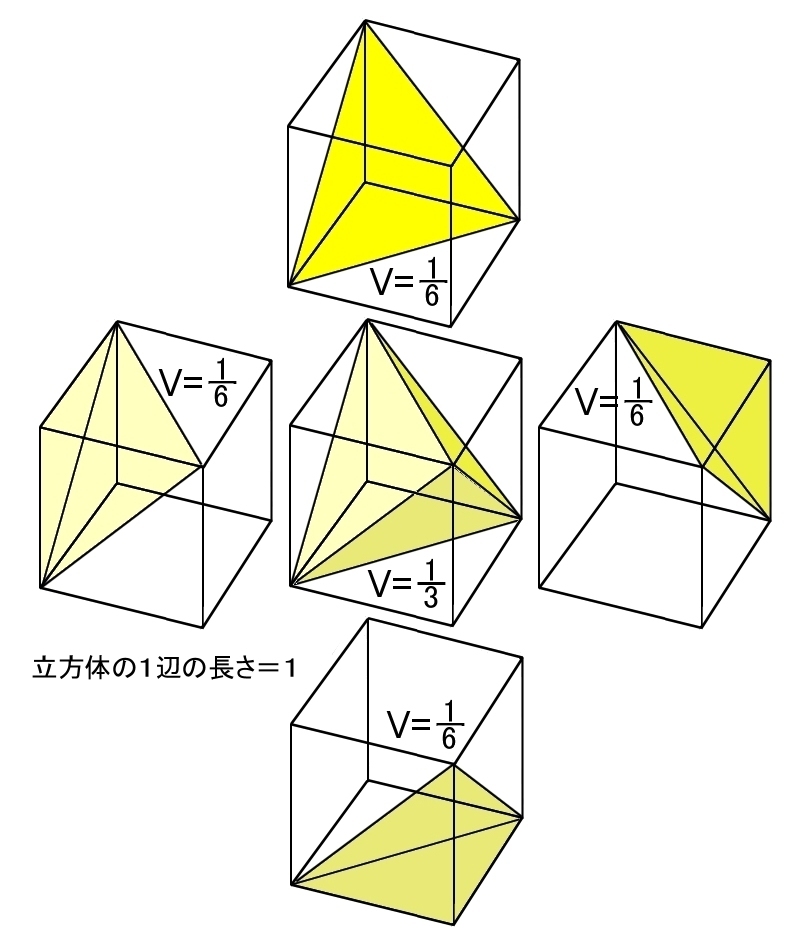
正四面体の体積＝1/3

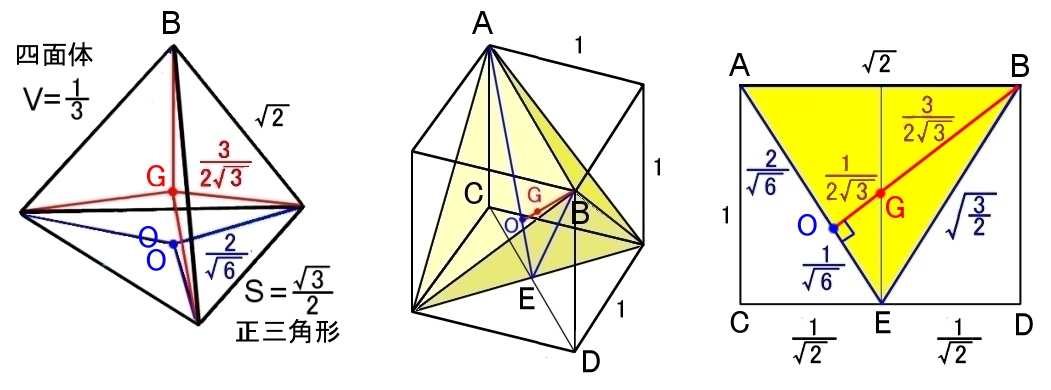
正四面体の頂点から重心までの距離＝ 3
2 3


［目次へ］



垂心が１点で交わることの証明　比較

その１　

BからACへの垂線とACとの交点をE，
CからABへの垂線とABとの交点をFとする。
また，この2本の垂線の交点をHとする。

このとき，A，H を通る直線がBCとD点で直角に交わることを示す。

図を参考に，

△CHE ∽ △CAF ∽ △BAE

であるから，

CE ＝ EH ，および， CF ＝ FA
CF FA BE EA

この２式より

AE ＝ EH
BE EC

この式から，

△BCE ∽ △AHE　　⇒　∠CBE ＝∠HAE

したがって，

△BCE ∽ △ACD

すなわち，△ACDは∠Dを直角とする直角三角形である。よってAD⊥BC　　　(終)


その２　　別証　　ダブルサークル


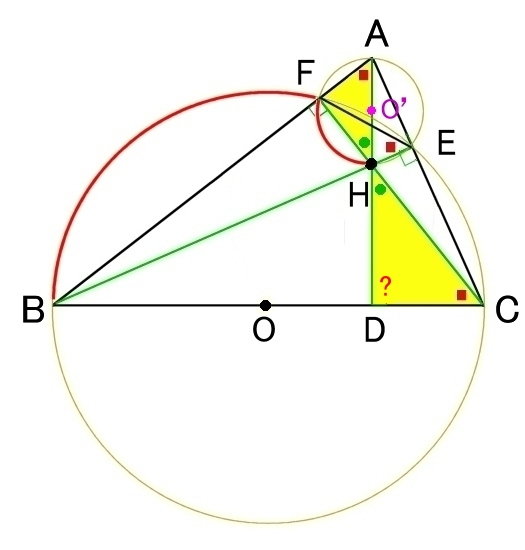
図を参考に
△CHDと△AHFが相似であることから∠CHD＝90°を示す。


その３　　別証　ダブルトライアングル


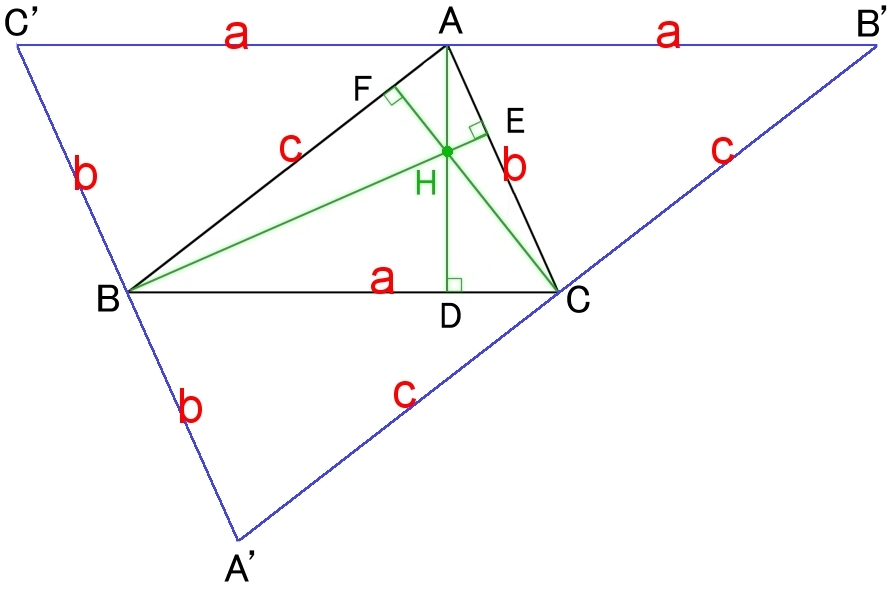
図を参考に
H が△A’B’C’の外心であることを示す。
すると，各辺の垂直二等分線AD，BE，CFは１点で交わる。