 |
B1 回転座標系とコリオリの力 |
| f-denshi.com [目次へ] 最終更新日:03/05/05 |
| サイト検索 |
[1] 直交座標系 Σ を正方向へ θ 回転した座標系を Σ'とします。平面上の点P のそれぞれの座標系での成分が,
| Σ 静止座標系で r = |
 |
x |
 |
| y |
| Σ' 回転座標系で R = |
 |
X |
 |
| Y |
とすると,正方向へのθ回転行列をP(θ)を用いて,r =P(θ)R ,(R =P(-θ)r )となります。成分では,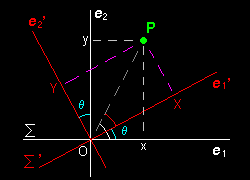
 |
x |
 |
= |
 |
cosθ |
-sinθ |
 |
 |
X |
 |
| y |
sinθ |
cosθ |
Y |
|
もし,時間t とともに座標系Σ' がΣに対して角測度ωで回転しているとすると,θ=ωt として,
 |
x |
 |
= |
 |
cosωt |
-sinωt |
 |
 |
X |
 |
・・・・ [*] |
| y |
sinωt |
cosωt |
Y |
[2] 時間 t で一回微分すると
 |
|
 |
=ω |
 |
-sinωt |
-cosωt |
 |
 |
X |
 |
+ |
 |
cosωt |
-sinωt |
 |
 |
|
 |
|
|
cosωt |
-sinωt |
Y |
sinωt |
cosωt |
|
もう一回微分すると,
 |
|
 |
=ω2 |
 |
-cosωt |
sinωt |
 |
 |
X |
 |
+2ω |
 |
-sinωt |
-cosωt |
 |
 |
|
 |
+ |
 |
cosωt |
-sinωt |
 |
 |
|
 |
|
|
-sinωt |
-cosωt |
Y |
cosωt |
-sinωt |
|
sinωt |
cosωt |
|
整理すると,
 |
|
 |
= |
 |
cosωt |
-sinωt |
 |
 |
|
 |
←少し工夫していますよ,注意! |
|
|
sinωt |
cosωt |
|
[3] この両辺に質量として m をかけ,ニュートンの運動方程式 ( F=mx''
) を思い起こせば,左辺は,
つまり,「静止座標系Σにおける力 f の各座標成分」と見ることができます。 一方,右辺の列ベクトルを,
 |
| −mω2X−2mω |
dY |
+m |
d2X |
|
|
| dt |
dt2 |
|
 |
= |
 |
FX |
 |
| −mω2Y+2mω |
dX |
+m |
d2Y |
|
|
| dt |
dt2 |
|
FY |
とおけば,これを「回転座標系から見た力F の各座標成分」とみなすことができます。なぜならば,回転行列を用いて,
 |
fx |
 |
= |
 |
cosωt |
-sinωt |
 |
 |
FX |
 |
| fy |
sinωt |
cosωt |
FY |
と表記できるからです。(↑ 回転する座標系間の座標成分の変換式[*]を参照して見てください。)
[4] ここで力が 0 である場合 ( fx=fy=FX=FY=0 ) を考察します。そのとき,運動方程式は各座標系で,
 |
mω2X |
 |
+ |
 |
|
 |
= |
 |
|
 |
[回転座標系]・・・・[**] |
| mω2Y |
|
|
| 遠心力 |
|
コリオリの力 |
|
|
となります。これを解くと,静止系ではよく知られているように等速直線運動
(x'=定数,y'=定数) を表す解が得られます。ところが,回転座標系で解くべき方程式は1回微分の項を含む複雑な2階微分方程式であり,一般には複雑な加速度運動が予想されます。
[**]のように書いた回転座標系の運動方程式の左辺が実在の力(重力,静電引力など)が存在しないもかかわらず
0 とならず,回転座標系では質点に加速度が生じているのです。この加速度を生じさせる見かけの力はふつう2つに分解して,
[**] の第1項を遠心力,第2項をコリオリの力
と呼びます。
[目次へ]

