| 13 ワイブル分布 | |
| f-denshi.com 最終更新日:11/10/8 | |
| サイト検索 | |
 [1] ワイブル分布とは,ワイブルという技術者が考案した分布なのでそのような名前が付いているが,その論文が出版されたのは統計学の歴史から見れば比較的新しく1939年である。ポアソン分布をポアソンが発表したのが1838年なので,100年の月日が経っている。
[1] ワイブル分布とは,ワイブルという技術者が考案した分布なのでそのような名前が付いているが,その論文が出版されたのは統計学の歴史から見れば比較的新しく1939年である。ポアソン分布をポアソンが発表したのが1838年なので,100年の月日が経っている。
材料の破壊強度に関わる統計データは正規分布に基づく解析にフィットしないことは当初から認識されていたようだ。材料の局所的に定義される強度がたとえ正規分布に従っていても,破壊は材料の最も弱い箇所に起因して一気に進むため,マクロ的な破壊現象に正規分布やその派生分布を適用しようとするとうまくいかないのだ。
ワイブルは,鎖の破断のメカニズムを念頭においてワイブル分布を考案した。1本の鎖の強度は構成される一つ一つのリングの強度の平均値や分散などで決まるわけではなくて,最も弱いリングの特性で決まるはずだと彼は考えた。
[2] リングがn個つながってできている1本の鎖を考え,一つのリングが加重xで切れる確率P(X≦x)を意味する累積分布関数を ,
G(x) = 1 - exp(-φ(x))
とおいてみる。φ(x)は任意の関数であるが,φ(x)=λx とおけば,G(x)は指数分布[#]と同形であり,xをジロー君のコップの使用時間と読み替えると,G(x)はジロー君がx時間後にコップを破損させている確率と考える[#]こともできる。つまり,コップの使用時間と鎖にかかる加重の大きさととを対応させて考えれば,上のような累積分布を仮定することに違和感は感じないだろう。
一方,鎖(のどこか)が加重 x で切断される確率を F(x) (累積分布関数)とすれば,鎖が切れない確率 1−F(x) は,
1 - F(x) = (1 - G(x))n
となる。これはn個のリングがいずれも切断していない(条件付き)確率と考えている。この式を書き直して,
F(x) = 1 - (1 - G(x))n = 1 - exp(-nφ(x))
となる。
nφ(x)= x−γ m α
α:尺度パラメータ
γ:位置パラメータ
m:形状パラメータ
と呼ばれる。
F(x)=1−exp − x−γ m [不信頼度] α
この分布関数は不信頼度と呼ばれる。3つものパラメータを導入すると,多くの事象について良く説明できるようになるのは当たり前のようでもあるが,各パラメータが具体的イメージに結びつけられているため,この分布を応用上重要なものとしている。
[3] 以下パラメータの意味を説明する。
パラメータαは名前のとおり加重の強さと確率を対応させるための変換尺度である。
γは加重がこの値以下であるならば,鎖の破損は実質的に起こりえない (G(x)≡0) とする閾値を表す。すなわち,
(1) γ>0: 加重γまで、破損は起こらないとする。
(2) γ=0: 加重を少しでもかけると破損の可能性が生じる。
(3) γ<0: 加重をかけずとも破損の可能性が存在する。
と意味づけられる。一方,F(x)を微分して確率密度関数を求めると,
f(x)= m x−γ m-1 exp x−γ m α α α
となる。これより,パラメータmによって,
(1) m>1: 破損確率密度はある加重で極大値をとる。
(2) m=1: 破損確率密度は指数関数的に減少していく。(=指数分布)
(3) m<1: 破損確率密度は急に減少し,初期に集中する。
というような特徴を持つ関数形がもたらされることになる。
ジロー君のコップの破損原因をワイブル分布で分析した結果,(1)m>1であれば,コップは時間とともに劣化が徐々に進み破損しやすくなると推察でき,(2)m=1であれば,コップの破損原因はもっぱらジロー君のそそっかしい性格に基づく不注意によることが多いと考えられる。また,(3)m<1であれば,コップにはあらかじめヒビが入っているなど初期不良の存在が考えられる。ジロー君の責任を追求できるのは(2)m=1の場合だけということになる。1年で3つもコップを割ることだけでジロー君を責めてはならないのだ。
実際にいくつかのmについてワイブル分布の形を示す。α=1/3,γ=0
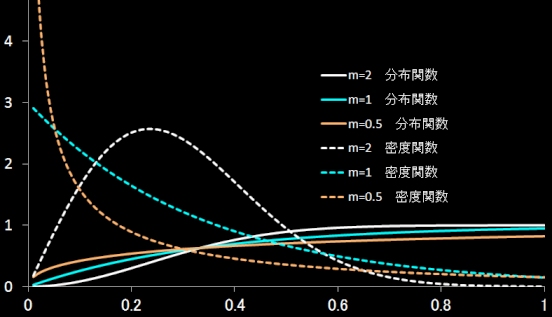
[4] さらに,
λ(x)= m x−γ m-1 [故障率] α α
R(x)= exp x−γ m [信頼度] α
が定義され,それぞれ故障率,信頼度と呼ばれ,確率密度関数 f(x),不信頼度(累積分布関数) F(x) とは,
f(x)=λ(x)R(x)
F(x)=1−R(x)
という関係にある。
注意: ワイブル分布には,次のような定義もあり,しばしば使われる。(分母にm乗がかかっていない)
F(x)=1−exp − (x−γ)m α
文献を読む際には定義がどのようであるかも確かめる必要がある。
Excelでの定義
引用する関数は,WEIBULL(x,α,β,TRUE) であるが,
F(x)=1−exp − x α β
として計算値が返される。γ≠0のときは自分でx軸方向にシフトさせて計算する。
ワイブル確率紙など実務的など応用の話は第2部で。