くっまんす王国　（１）　　
f-denshi.com  最終更新日：11/06/25
サイト検索
ここまでの標本統計用語について具体例で確認することがこのページの目的。　

［１］　クマンドロメダ大星雲の第９８惑星では，くまが知的生命体として進化を遂げていた。その惑星の極東の人口５人の国，「くっまんす王国」を統計分析してみよう。この国の各人ωの収入を確率変数X(ω)とし，とり得る値を

　　｛X(ω)｜１，２，４，５，８｝　　　　　［母集団］
とする。通貨単位は円らしいが，それではしみったれているので，１億円，２億円，４億円，５億円，８億円としておく。ただし，ゼロがたくさん並ぶと計算間違いしそうなので上記のまま書くこととする。 なお，X(ω)は簡単にXとだけ書くこともある。また，ω＝ジロー，ウメ，コタ，サブ，ウンペであり，ジロー君が国王である。すると，この国の住民を無作為に選び出したとき，収入，X(ω)＝x＝1,2,4,5,8　が実現する確率はいずれも５分の１(＝0.2)と考えればよく，確率密度関数，f(x)＝P(X=x)は次のようになる。

ここでは，P(X)を点だけではなく，後々のことを考慮して，その面積の総和が１となるような棒グラフとして示した。

さて，次にこの国の平均収入を計算しよう。それはこの国の住民の収入の期待値であり，

　E(X)＝ xP(X=x) ＝1× 1 ＋2× 1 ＋4× 1 ＋5× 1
＋8× 1 ＝4
5
5 5 5 5

と計算される。これは母集団の期待値とか母平均と呼ばれ，μという記号がしばしば使われる。

［２］　次に各住民の年収のばらつきの目安として，平均値からの差の２乗をすべて合計し，住民の数で割った値V(X)を次のように定義する。

　V(X)＝E({X−E(X)}2)
　　＝(1−4)2× 1 ＋(2−4)2× 1 ＋(4−4)2× 1 ＋(5−4)2× 1
＋(8−4)2× 1
5
5 5 5 5

　　　＝　6　　　　　　　　　　[母分散] これは母集合の分散ということで，母分散と呼ばれ，σ2という記号がしばしば用いられる。さらに母分散の平方根をとると，  

σ＝ 6 ≒2.4　　　　　　［母標準偏差］
となるが，これは母集団から計算されることを意識して，母標準偏差と呼ばれる。

つまり，「くっまんす王国」の平均収入は４億円であるが，各住民の収入にはバラツキがあり，平均値から２.４億円ほどずれているというのが，この国の収入分布の特徴ということである。

以上は集合全体＝母集団を正確に捉まえた計算である。

［３］　この例では住民の数がたった５人の国なので，母平均，母標準偏差を直接簡単に計算することができた。しかし，人口１億人の国となるとそう簡単にはそれらを求めることはできない。そこで全体の一部分を取り出して調べ，全体を推測するということが現実的な対応となる。新聞社などが政党支持率などを無作為抽出で調べるやり方だ。ここではそのやり方を「くっまんす王国」について適用してみよう。  

最初に特別な場合として，重複しないようにすべての住民の収入を選び，それを足して人数で割ると，

x~　＝ 1＋2＋4＋5＋8 　　　(　≡　x~　加算平均　）
5
　　　＝　4　　　　

となるが，これは母平均と一致する。すばらしい発見のようだが，これは少し考えるとあまり意味がない。すべてを調べ上げることができるのならば，先程示したように正確な母集団の期待値＝母平均を最初から計算すれば済む事だからだ。

つぎに，「くっまんす王国」５人全員の収入を調べるのは大変だということにして手を抜き，その一部の２人を無作為に選び出して調べるという手法を考える。無作為ということは，５人のうちで誰が選ばれるかはすべて同じ確率で等しいということ。 これは１人目を選び出すときはもちろん，２人目を選び出すときも５人全体の中から無作為に抽出を行うということである。すると，その２人の収入の組み合わせ(標本値とか実現値，もしくはタダの標本ともいう)は次の25通りとなる。   (「標本」という用語は，ややあいまいな意味に使われている。)

大きさ2の標本 　　大きさ2の標本(値)たち25個
(X1,X2)　　　　＝　　　　(x1,x2)
標本(変量)　　　　　　　　　標本(値)

（1,1），(1,2) ，(1,4) ，(1,5) ，(1,8)
（2,1），(2,2) ，(2,4) ，(2,5) ，(2,8)
（4,1），(4,2) ，(4,4) ，(4,5) ，(4,8)
（5,1），(5,2) ，(5,4) ，(5,5) ，(5,8)
（8,1），(8,2) ，(8,4) ，(8,5) ，(8,8)
ここで，(4,5)という記号は，選ばれた２人の収入が「１人目が４億円，２人目が５億円」という意味。また，上の25通りのうち，どの組み合わせが選び出されるれるかは，２人が無作為に選ばれている限り同じ確率２５分の１であり，それら一つ一つが「標本値」ということだ。新聞社などの行う世論調査とは１億人もの中から1000人ほどを選び出し，それを一つの標本値として解析しているわけである。

また，この一覧では，(1,1)，(2,2)のように同じ住民の収入が重複して選ばれているが，これは１人目に誰が選ばれたかに関係なく２人目も５人全体の中から選び出したためで，このような選び出し方を統計学では「復元抽出法」という。これは２次元の同時確率分布とみなせるが，２つの確率変数，X1,X2はともに同じ標本空間上の確率変数であり，かつ，X1とX2は独立しているという状況にある。

初めてこの選択方法を聞くと，同一の住民からなるデータ(1,1)などが含まれることに違和感を覚えるが，実は２人とも別人を選ぶ方が不自然な選び方ともいえる。なぜならばそのように選ぶためには，２人目の選択は１人目を除外した残り４人の集合から選び出すこととなるが，その方がむしろ恣意的な選び方となり，数学的な取り扱いも簡単ではなくなるのだ。

［４］　さて，「くっまんす王国」の各標本値(x1,x2)ごとの平均値や標準偏差を求めてみよう。例えば，全日本経済新聞社が２人をサンプリングして得た標本値が(2,5)，フジエダ電子出版社のそれが(8,8)であれば，

(2＋5)÷2＝　3.5億円　　全日本経済新聞社 　
(8＋8)÷2＝　8.0億円　　フジエダ電子

が各社の選び出した標本値の平均値で標本平均値である。一般的な世論調査の平均とは統計学用語を用いれば，標本平均値というワケだ。  

X~＝ X1＋X2 　　　　大きさ２の標本平均
2
x~＝ x1＋x2 　　　　大きさ２の標本平均値
2
大きさn=2のすべての標本平均値たち，x~＝(x1＋x2)/2についての計算結果を示すと，  
標本平均 X~　(　25個の標本平均値たちx~　)

1.0 ，1.5 ，2.5 ，3.0 ，4.5 　
1.5 ，2.0 ，3.0 ，3.5 ，5.0 　
2.5 ，3.0 ，4.0 ，4.5 ，6.0　　　 　
3.0 ，3.5 ，4.5 ，5.0 ，6.5 　
4.5 ，5.0 ，6.0 ，6.5 ，8.0
となる。これら25個のx~ はどれも等確率で実現するが，同じx~ について実現確率をひとまとめにして表示すると，
P(X~=1.0)＝1/25
P(X~=1.5)＝2/25
P(X~=2.0)＝1/25
P(X~=2.5)＝2/25
P(X~=3.0)＝4/25
P(X~=3.5)＝2/25
P(X~=4.0)＝1/25
P(X~=4.5)＝4/25
P(X~=5.0)＝3/25
P(X~=5.5)＝0/25
P(X~=6.0)＝2/25
P(X~=6.5)＝2/25
P(X~=7.0)＝0/25
P(X~=8.5)＝0/25
P(X~=8.0)＝1/25
P(上以外)＝0

となる。離散的確率関数のP(X~)の分布は厳密には点で示すしかないが[#]，ここでは棒グラフの内部の面積に確率の意味を付与できるように，棒の高さ：P(X~)×n，棒の幅：1×（1/n）とする新しい図で描き直すことにする。このようにすれば，棒グラフの面積の総和は１とすることができる。そして，後ほど述べることとなる連続確率変数で定義される確率密度関数との対比がビジュアル化できる。以下，そのように描いた 2P(X~) の確率密度分布を示す。

　　
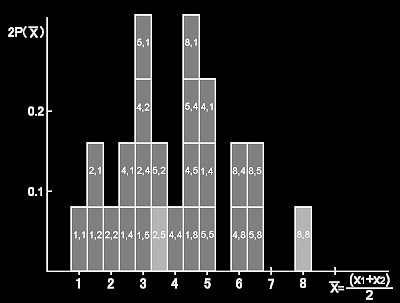
標本平均値たちを小さい順番に並べたとすると，一番最後の25番目にくるのがフジエダ電子出版の選び出した標本値に対応する標本平均値で，分布全体の左から96-100％(または右から0-4％）のところに位置していることがわかる。一方，全日本経済新聞社の標本値は小さい方から11-12番目にあり，分布の左から40-48％のところに位置している。また，ちょうど真ん中にある13番目の標本値(4,4)は分布の48-52％のところに存在すると述べることができる。このような見方はこれから統計学的な推定を考えていく上での基本となる。

［５］　それにしても「フジエダ電子出版」の調査結果は変だ。「くっまんす王国」の平均収入は８億円，標準偏差はゼロ，つまり，この統計ではすべての国民が８億円の収入を得ていると推測することになる。答えを知っている者から見ると，こんな調査，信用できやしまへんとなる。真の値である母平均４億円，母標準偏差２．４億円からあまりにかけ離れているではないか。この標本値は上の分布の中で一番端っこ(大きい方から0-4％)のところに外れて位置しているのでなんかオカシイと感じるのである。

しかし，上の方法によるサンプリング調査では，25回に１回はこのような結果となってしまうのは数学的に避けられないのだ（フジエダ電子出版の言い訳）。  

サンプリング調査の平均値がどれだけ真実とずれてバラついているかを評価するためには25個の標本平均値たちの平均や分散を計算するとよい。まず，標本平均(値たち)の平均値(期待値)だが，ここでは定義に忠実に計算すると， 

E(X~)＝(1.0・P(X=1）＋1.5・P(X=1.5)＋・・・・・＋8・P(X=8)　
　　　　＝4　　　［標本平均の期待値］
となり，母平均E(X)=μ=4と同じとなる。これは，E(X~)＝E((X1＋X2)/2)＝E((X1)/2＋E(X2)/2)＝4/2＋4/2＝4と計算して示す方がスマートだ。この関係：母平均E(X)＝標本平均の期待値E(X~)は常に成り立つ重要な関係である。

次に「標本平均たちの分散」を計算する。これもベタで計算すると，

V(X~)＝(1.0-4)2P(X~=1.0)＋(1.5-4)2P(X~=1.5)＋･･･＋(8.0-4)2P(X~=8.0)　
　　　　＝3　［標本平均の分散］
となる。つまり，母集団の分散，６の半分である。この関係 V(X~)＝σ2/n，(n=標本の大きさ) も一般的に証明できる[#]ことで，母集団の中からn個を復元抽出して作った標本値たちの分散は，母分散のn分の１となる。

分散ではなく，標準偏差を比較する場合は，標本標準偏差は母標準偏差の√n分の１ということになる。  

これが意味することは，n⇒無限とすると，標本標準偏差⇒ゼロ　ということである。つまり，サンプリング人数を増やせば増やすほど，バラツキは√n分の１に逆比例して小さくすることができるということだ。   これは大数の法則と呼ばれる。

［６］　さらに各標本(値)ごとの分散は標本分散と呼ばれる。n=2の場合の定義は以下のとおり。

S2≡ ((X1-X~)2＋(X2-X~)2) 　　　　大きさ２の標本分散
2

標本平均値の分散と紛らわしいが別モノである。先の２社の選んだ標本について計算すると，  

S2≡ ((2-3.5)2＋(5-3.5)2) ＝2.25　　[全日本経済新聞]
2
S2≡ ((8-8)2＋(8-8)2) ＝0　　　　　　　[フジエダ電子]
2

  という結果になる。これから標本標準偏差(値)と呼ばれる量は次のように計算される。  

S＝ 2.25 ＝1.5　　　　 [全日本経済新聞]
S＝ 0 ＝0   　　　　　[フジエダ電子出版]

具体的な25個の標本(値)について標本分散の計算結果を一覧に書いておくと，

標本分散 S2　　　　25個の標本分散たち

　 0.00 ，0.25 ，2.25 ，4.00 ，12.25
　 0.25 ，0.00 ，1.00 ，2.25 ，9.00
　 2.25 ，1.00 ，0.00 ，0.25 ，4.00
　 4.00 ，2.25 ，0.25 ，0.00 ，2.25
　12.25 ，9.00 ，4.00 ，2.25 ，0.00

これからS2の期待値を計算すると，

E(S2)＝(0.00×5/25＋・・・・＋12.25×2/25
　　　　＝3.00

この結果は，V(X~)＝σ2/2＝E(S2)であるが，これはタダの偶然である。一般に大きさｎの標本について，

V(X~)＝ σ2 　，　　E(S2)＝ n−1 σ2
n n

となる[#]。今，n=2なので，これらはたまたま一致する(=1/2)わけ。

さらに標本分散たちの分散を考えることもできて，

V(S2)＝((0.00−3)2×5/25＋・・・・＋(12.25−3)2×2/25
　　　　＝13.35

となる次第。計算は各自で確認せよ。くっまんす王国の国王がジロー君であることも覚えておいてほしい。




［目次］