 |
13 広義積分 |
|
| f-denshi.com [目次] 最終更新日:07/06/09 |
| サイト検索 |
|
1.広義積分
[1] 広義積分 (improper integrals) とはリーマンの定積分における定義において,
| (I) 積分区間は閉区間 [a,b] |
⇒ |
[a,∞],[-∞,a],[-∞,∞] でもOK |
| (II) 被積分関数|f(x)|<∞ on [a,b] |
⇒ |
f(x0)=∞ ,x0∈[a,b] でもOK
|
のように緩和(拡張)した積分で,例えば,
| (1) |
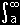 |
|
dx (a>0) |
| (2) |
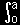 |
| 1 |
|
|
|
 |
x |
|
|
dx (a>0) ( f(0)=∞ です。) |
などがあります。ここでの積分記号の意味はなんとなくわかると思いますが,厳密な広義積分の定義に従うと,
| (1) |
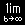 |
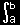 |
1 |
dx= |
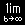 |
 |
-1 |
− |
-1 |
 |
= |
1 |
|
|
|
|
| x2 |
b |
a |
a |
| (2) |
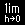 |
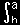 |
| 1 |
|
|
|
 |
x |
|
|
dx= |
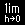 |
2・ |
 |
|
|
 |
a |
|
− |
|
|
 |
h |
|
 |
=2 |
|
|
 |
a |
|
というように定積分と極限とを組み合わせて計算することを意味しています。
| [2] 広義積分では |
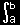 |
f(x)dx が収束しても |
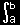 |
|f(x)|dx が収束するとは限りません。 |
しかしながら,その逆は成り立ち,
|
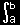 |
f(x)dx |
|
≦ |
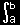 |
|f(x)|dx |
|
|
なる関係があります。このとき,f(x)の積分は絶対収束するといいます。
まず,リーマン積分について,
しばらく,執筆中断 ・・・。
[ 目次へ ]
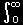 |
|
dx= |
|
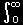 |
|
dx= |
π |
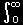 |
e-ax2 |
= |
|
|
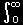 |
e-x2 |
= |
|
Γ(1/2) Γ関数 |
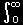 |
x2n+1e-ax2 |
= |
|
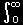 |
x2ne-ax2 |
= |
|
|