| t117 理想ボース気体 | |
| f-denshi.com 更新日: 22/01/29 校正中 | |
| サイト検索 | |
| 目次へ | |
[1] 復習から始めます。すでに示したように [#],同一種類のボース粒子に対する大配関数は,
Ξb = ∞ Ξjb ボース粒子の大分配関数 Π j=1
ただし,
Ξjb = 1 1−exp { -(εj−μ)/kT}
= 1 1−ξexp (-εj/kT)
と表すことができて, j はすべての固有状態 (エネルギー準位)εj に対して取ります。固有状態が縮退してるときは,エネルギー準位εj の縮退度をΔj とすれば,
Ξjb = Δj 1−exp {-(εj−μ)/kT}
= Δj (ξ≡eμ/kT ) 1−ξexp (-εj/kT)
また,ボース分布関数は,
fB(εj )=<nj >b= Δj exp{(εj−μ)/kT}−1 = Δj ξ-1exp (εj/kT)−1
と書くことができました。
ボース分布関数は各エネルギー固有値εj を占める粒子数を意味し,必ず正の値 fB(εj) > 0 をとらなければならないことから,
εj−μ > 0
でなければなりません。
[2] 化学ポテンシャルがμ (絶対活量がξ ) であるとき,粒子数の期待値は,
<N>= <nj>b= Δj ξ-1exp (εj/kT)−1
系のエネルギーは,
E = <εj >b = εjΔj (2.238) ξ-1exp {εj/kT}−1
で与えられます。また,グランドポテンシャルは,
J = kT logΞb =kT Δj log { 1−ξexp (-εj/kT) }
圧力は,
P=− J =− kT Δj log { 1−ξexp (-εj/kT) } (2.240) V V
と計算することができます。
[1] さて,ここではエネルギー固有値が連続的に分布するものとして取り扱うために,エネルギーの関数としての状態密度 D(ε) を用いて各期待値の積分形を次のように表す(近似する)こととします。(ε≧ 0)
N = D(ε) dε (2.241) ξ-1exp (ε/kT)−1
E = εD(ε) dε (2.242) ξ-1exp (ε/kT)−1
J = +kT D(ε) log { 1−ξexp (-ε/kT) }dε (2.243)
P =− kT D(ε) log { 1−ξexp (-ε/kT) }dε (2.244) V
さらに, D(ε) として,3 次元自由粒子に対する1粒子状態密度 [#],
D(ε) =2πV 2m 3/2
ε ( ε≧0 ) (2.245) h2
を代入して計算することにしますが,この分布に従う粒子集団を理想ボース気体といいます。
[2] ここで,一つ注意しなければならないことは,エネルギーε= 0 のとき,(2.245) ではD(ε) = 0 となり,(2.241) 式以下の積分において,0 とカウントされてしまいます。フェルミ分布の場合は,一つの状態には高々1 つしか粒子が入りません (スピンを考慮する場合でも,一つのεに対して高々2個) から,アボガドロ数程度の粒子数を扱うときは最低エネルギー準位を無視したとしても統計量の計算結果にほとんど影響がありません。
しかし,ボース粒子の場合は,一つの状態にいくつでも粒子が入ることが可能なため,系の全エネルギーが低いときは最低エネルギー準位に無視できないほどの数の粒子が占有している状態も起こりえます。したがって,(2.241)式以下のような積分近似がいつも成り立つわけではありません。
図2.9: フェルミ統計では最低準位を占有する粒子は高々1つ,
スピンを考慮しても2つであるが,ボース統計では最低準位に
系の巨視的な数の粒子が占有することも起こり得る。
そこで,D(ε) として (2.245) をエネルギーεに関する積分に適用する際は,最低準位にある粒子数 N0 だけを別に抜き出して,(2.241) 式は次のように書くことにします。
N =2πV 2m 3/2
ε dε+N0 (2.246) h2 ξ-1exp {ε/kT}−1
ここで,N0 は,
N0 =<n0>b = 1 = ξ (2.247) ξ-1exp { 0/kT}−1 1−ξ
と表すことが可能です。さらに,(2.246) 式を変形した,
N−N0 =2π 2m 3/2
ε dε V h2 ξ-1exp {ε/kT}−1
において,ε= kTx, dε= kTdx と変数変換をすれば,
N−N0 = 2 2πmkT 3/2
x dx (2.249) V
π h2 ξ-1ex−1
ここで,
λ(T)= h = 2π h21/2 熱ドブロイ波長
2πmkT mkT
[3] および,
ボース-アインシュタイン積分
特に
|
を導入すると,(2.249) は,
N−N0 = b (3/2,ξ) (2.253) V λ(T)3
と表せます。ボース-アインシュタイン積分 b (3/2n, ξ ) は 0≦ξ≦1 において有界な増加関数ですが,後々の計算の便宜を考えて,(2.249),または,(2.253) で,ξ=1 つまり,μ=0 であるとき,N0=0 となる温度を臨界温度 Tc と定義します。すなわち,
N = b (3/2,ξ) ⇔
Tc= h2 N 2/3 2πmk b (3/2,1)V V λ(Tc)3
によって Tc を定義します。すると,(2.253) を (2.254) で除して,
N−N0 =N b (3/2,ξ) λ(Tc)3 = b (3/2,ξ) T 3/2 (2.256) N b (3/2,1) λ(T)3 b (3/2,1) Tc
これを (2.247) を用いて,N0 を再びξ に戻してやれば,
N = N b (3/2,ξ) T 3/2 + ξ (2.257) b (3/2,1) Tc 1−ξ
原理的には,これをξ について解けば,ξ の温度の関数,つまり,化学ポテンシャルを温度
の関数として求めることができるはずです。
[1] 残念ながら,積分方程式 (2.257) は数値解析に頼らないと解くことはできません。しかし,厳密解を知らなくても上の関係式は際立った特徴をもっているので,それを確認しておきましょう。まず,(2.257) を N (1モル程度の量を考える)で割り,その右辺を,
1= b (3/2,ξ) T 3/2 + 1 ξ ≡yT(ξ) (2.258) b (3/2,1) Tc N 1−ξ 第1項 第2項
とすれば,この関数 y=yT (ξ) と y=1 との交点が求めるべきξ の解となります。yT (ξ ) の概略を,T>Tc,T=Tc,T<Tc の3 つの場合に分けて図示すると図2.10 のようになります。第1項はξの単調増加関数です。一般的にN が1023 程度の数であることを考慮すれば,yT (ξ)第2項の分母 1−ξ は〜10-23,すなわち,ξが 1 に極めて近い 1 より小さな数であるときを除いて,第2項=N0/N=0 とみなすことができます。そのとき,T>Tc ならば,
[第1項]= b (3/2,ξ) T 3/2 =1 [ T>Tc ] (2.259) b (3/2,1) Tc
は 0<ξ<1 に解をもち,例えば,図の a 点のξの値となります。
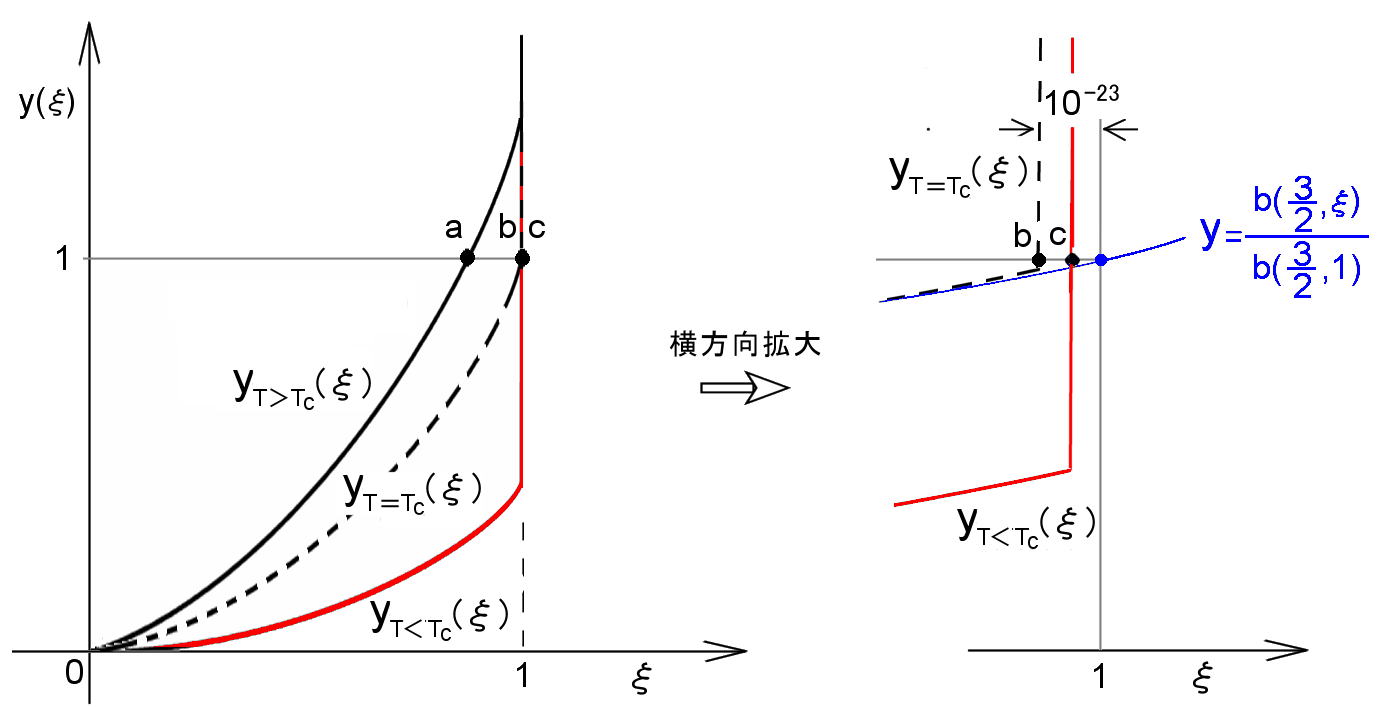 |
| 図2.10: 方程式 (2.258) が解をもつ範囲を示した。特にT≦Tc であるとき,解は(1−1/N) < ξ < 1 の範囲に解が集中する様子が分かる。 |
[2] 一方,T≦Tc であるときは,0<ξ<1 の範囲で (2.258) 式の第1項< 1 ですから,yT (ξ ) が y=1 と交わるためには,第2項からの寄与が不可欠で,それは,0<(1−ξ)<10-23 の範囲にあるときに実現(=解をもつ) します。また,その第2項の寄与が急激な増加関数であるため,このyT (ξ) はξ=1 の1/N ほど左側 (マイナスより) からほぼ垂直に切り立った関数形となっています。そのようなξの範囲 ( 1−10-23<ξ≦1 ) ではb (3/2, ξ)≒ b (3/2, 1) と近似ができ,(2.258) は次のようになります。
T 3/2 + 1 ξ = 1 [ T≦Tc ] Tc N 1−ξ
このとき,(2.247) 式であることを思い出せば,この関係式は,
| N0 | =1− | T | 3/2 | ⇔ N−N0=N | T | 3/2 | (2.261) | |||||||
| N | Tc | Tc |
と書くことができ, 温度,T≦Tc において最低エネルギー固有状態が巨視的な数の粒子によって占められている割合を表す式であることがわかります。この関係を図示すると図2.11となります。
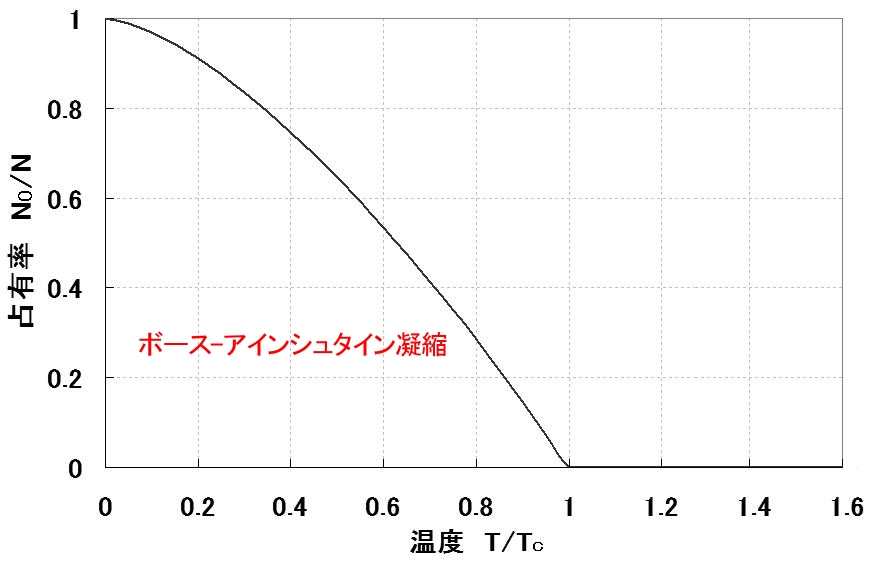 |
| 図2.11: 全粒子数N に対する最低エネルギー状態にある粒子数 N0 の割合。 温度 (T<Tc において,N0 が巨視的な数 (≒N) となる(ボース-アインシュタイン凝縮)。 |
[3] このようにT<Tc の温度領域では,化学ポテンシャルμ≒- 0 において,最低エネルギー固有状態に巨視的な粒子が占有する熱平衡状態が存在します。この状態をボース-アインシュタイン凝縮と呼びます。これは低温での金属の超伝導や4He の超流動発現に重要な役割を果たしていると考えられています。
この図に関する注意点を述べておくと,臨界温度 Tcはヘリウムであれば,4K程度であり,この温度を超えて冷却させていくと絶対零度に向けて一気に巨視的な量(数 g であれば2023個)の原子が最低準位の状態を占めるように変化するという劇的な変化 (転移) が起きるということです。
[1]
圧力
圧力も粒子数と同様に最低エネルギー準位の寄与だけ別に考慮する必要があろうかと考えられます。 (結論としては必要ないのであるが) そのためには (2.240) 式のε0=0 とした項,
P0 =− kT log (1−ξ) V
を別に付加する必要があります。したがって,(2.245) を(2.244) に代入した式にP0 を付加し,
| P=−2πkT | 2m | 3/2 |
|
log { 1−ξexp (-ε/kT) }dε+P0 (2.263) | ||||||||
| h2 |
と積分表示を書くことにします。
これを部分積分すると,
| P=[0となる項]+2πkT | 2m | 3/2 |
|
ξexp (-ε/kT) | dε+P0 | ||||||||||||
| h2 | 1−ξexp (-ε/kT) | kT |
| = | 4 | πkT | 2m | 3/2 |
|
1 | dε+P0 | ||||||||||||
| 3 | h2 | ξ-1exp {ε/kT}−1 | kT |
さらに,ε=kT x,dε=kTdx と変数変換を行い,ド・ブロイ波長:λ(T) = h/(2πmkT)1/2 で置き換えれば,
P =kT 4 πkT 2πmkT 3/2
x x dx+P0
3 π h2 ξ-1ex−1
=kT b(5/2,ξ) − kT log(1−ξ) λ(T)3 V
第1項と第2項を比較すると,1−ξ が 1/N であったとしても,log(1−ξ ) は高々10 のオーダーなので,V/λ(T) 3 >> 10 であることを考えれば,第2項の寄与は全圧力に対して無視してよいことが分かります。すなわち,
P=kT b(5/2,ξ) [任意温度] (2.266) λ(T)3
[2]
状態方程式
T>Tc では,(2.253) 式において N0=0 として,
N=V b(3/2,ξ) [ T>Tc ] (2.267) λ(T)3
(2.267) 式を用いて,(2.266) 式からλ(T) 3 を消去すると,
PV=NkT b(5/2,ξ) [ T>Tc ] (2.268) b(3/2,ξ)
が得られる。一方,(2.256) 式で,N0=0 として,上の式から b (3/2,ξ) を消去すると,
PV=NkT b(5/2,ξ) T 3/2 [ T>Tc ] b(3/2,ξ) Tc
=NkT b(5/2,ξ) T 3/2 [ T>Tc ] ζ(3/2) Tc
T≦Tc では,(2.253) を用いて,(2.266) 式から,λ(T) 3 を消去し,ξ=1 とすれば,
PV=(N−N0)kT b(5/2,1) T 3/2 ( ≒ 0.51 (N−N0)kT ) b(3/2,1) Tc
=NkT ζ(5/2) T 3/2 [ T≦Tc ] ζ(3/2) Tc
ここで,2 つ目の = では,(2.261) 式を用いています。これから,ボース理想気体は修正古典理想気体に比べて低い圧力を示すことが分かります。特に最低準位にある粒子はまったく圧力には寄与しません。これは一つの状態を多数の粒子が占有するときは,粒子数に比例する圧力を発生させないためです。
[3]
エントロピー
J =−PV,および,低温 T≦Tc における状態体方程式 (2.270) を用いると,
S=− ∂J V,μ =Nk 5ζ(5/2) T 3/2 [ T≦Tc ] ∂T 2ζ(3/2) Tc
高温の場合は,(2.269) を T で微分して求めます。
[4]
全エネルギー
内部エネルギーについては (2.249) 式を導いたときと同様な変数変換を行うと,
E = 2πV 2m 3/2
ε ε dε h2 ξ-1exp {ε/kT}−1
= 3 ・ 4 kTV 2πmkT 3/2
x x dx 2
3 π h2 ξ-1ex−1
= 3kTV b(5/2,ξ) [任意温度] 2λ(T)3
と計算を進めることができます。この式と,(2.266) と比較して,
E= 3 PV [任意温度] 2
の関係もわかります。さらに,(2.253) 式を用いて,(2.272) からV/λ(T) 3 を消去すると,
E= 3 (N−N0)kT b(5/2,ξ) [任意温度] 2 b(3/2,ξ)
T<Tc ではμ=0 (ξ=1) であるから,b (5/2, ξ)→ζ(5/2) とし,(2.261) も用いて,
E=Nk 3ζ(5/2) T 3/2 T [ T≦Tc ] 2ζ(3/2) Tc
3ζ(5/2) = 0.770 2ζ(3/2)
自由エネルギー
T≦Tc 凝縮相においては,G=μN=0 であり,
J = F−μN
= F
=−PV
=−2E/3
=−2ST/5
=−NkT ζ(5/2) T 3/2 ζ(3/2) Tc
が成り立っている。
[5]
比熱
次に比熱ですが,低温の場合,(2.275) 式から,
Cv = ∂E N,V ∂T
= 15 Nk ζ(5/2) T 3/2 [ T≦Tc ] 4 ζ(3/2) Tc
低温でのボース気体の比熱はT の3/2 乗に比例することが分かります。転移温度,T=Tc のときは,上式から,
Cv 15ζ(5/2) =1.925 [ T=Tc ] Nk 4ζ(3/2)
が得られます。T>Tc のときは,(2.274) において,N0=0 として,
E= 3 NkT b(5/2,ξ) 2 b(3/2,ξ)
と近似します。これより,
Cv = 1 ∂E N,V ∂ T 3b(5/2,ξ) N,V Nk Nk ∂T ∂T 2b(3/2,ξ)
= 3b(5/2,ξ) + 3T ∂ b(5/2,ξ) N,V ∂ξ N,V 2b(3/2,ξ) 2 ∂ξ b(3/2,ξ) ∂T
↓ ∂ξ N,V =− 3ξb(5/2,ξ) ∂T 2T b(3/2,ξ)
| = | 3b(5/2,ξ) | + | 3T | b(3/2,ξ)2−b(5/2,ξ)b(1/2,ξ) | -3ξb(5/2,ξ) | ||||||
| 2b(3/2,ξ) | 2 | ξ b(3/2,ξ)2 | 2T b(3/2,ξ) |
= 3b(5/2,ξ) − 9 b(3/2,ξ) − b(5/2,ξ) 2b(3/2,ξ) 4 b(1/2,ξ) b(3/2,ξ)
= 15b(5/2,ξ) + 9b(3/2,ξ) [ T>Tc ] 4b(3/2,ξ) 4b(1/2,ξ)
途中で微分公式,
∂ b(n,ξ)= 1 b(n−1,ξ) 及び, ∂ξ N,V =− 3ξ b(3/2,ξ) ∂ξ ξ ∂T 2T b(1/2,ξ)
を利用しています。以上の結果を図示すると図2.12 となります。ボース理想気体もフェルミ気体と同様に,高温極限においては古典気体の比熱
Cv = (3/2)Nk に近づきます (デュロン-プティーの法則) が,温度を下げていくと,比熱は転移温度の近くで比熱に寄与する粒子数が増加するため,古典理想気体の比熱より大きな値をとりますが,さらに転移温度を超えて温度を低下させると,比熱に寄与しないエネルギー 0 の粒子が増えるため,温度の 3/2 乗に比例して比熱は低下し,絶対零度ではゼロとなります。そのためボース気体は転移温度 Tc で比熱が最大になることが分かります。液体ヘリウム4He では,常流動から超流動へ転移する温度で比熱の発散が観測されており,超流動体がボース流体であることの一つの根拠と考えら
れています。
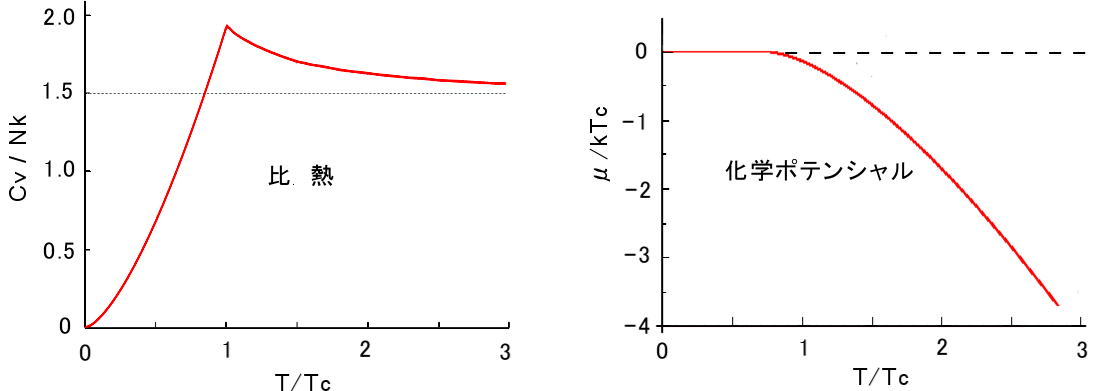 |
| 図2.12: ボース気体の比熱と化学ポテンシャルの温度依存性。 |
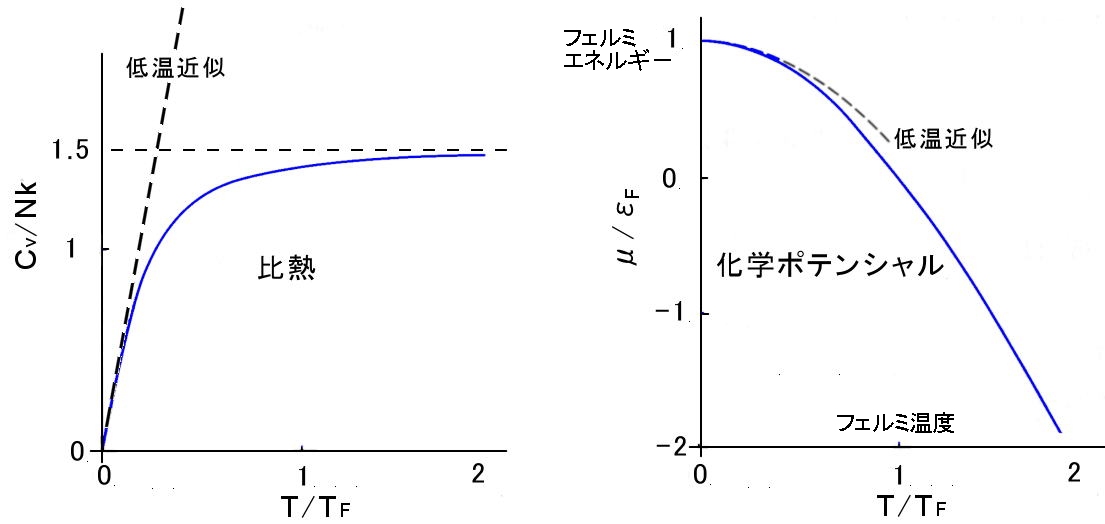
フェルミ気体との比較
 |
|
フェルミ気体の比熱と化学ポテンシャルの温度依存性。 |
SUSTAINABLE TOKIWADAIGAK SINCE 2002
S=Nk 5ζ(5/2) [ T=Tc ] 2ζ(3/2)
数学的捕捉
